Математика первый семестр 2012-13

Задачи и вопросы по курсу математики для студентов-энергетиков 2012-2013 уч.г., первый курс, первый семестр , лектор доц. Братчиков А.В. ( три страницы )

1. Записать комплексные числа в тригонометрической и показательной формах , , , .

2. Найти корни 3 степени из комплексного числа .

3. Решить квадратное уравнение .

4. Вычислить, представив комплексное выражение в алгебраической форме .

5. Вычислить матричные выражения , где , , .

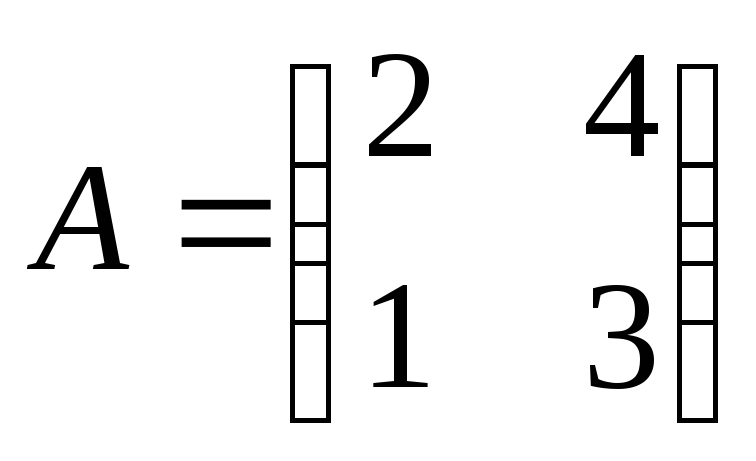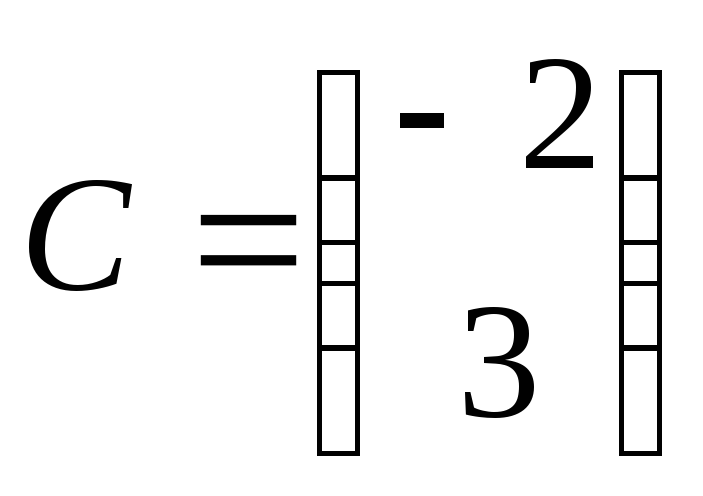6. Вычислить определитель разложением по четвёртой строке.

7. Найти собственные числа и собственные векторы матрицы .

8. Решить методами Крамера, Гаусса и матричным систему линейных уравнений

9. Вычислить векторное выражение 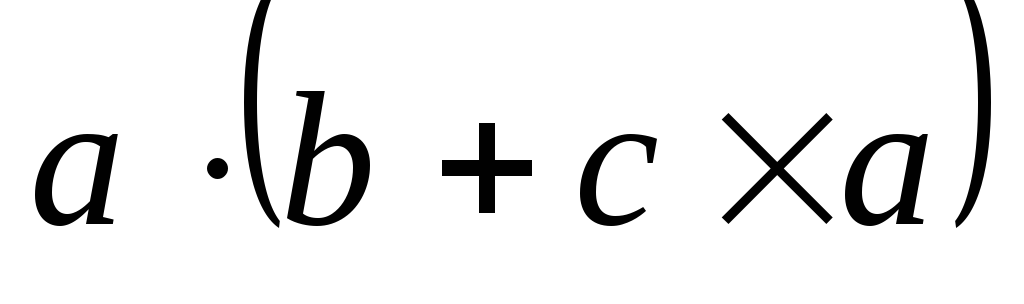, если ,.

10. Найти уравнение прямой L, проходящей через точку M(1, -1,) перпендикулярно отрезку AB, если и .

11. Составить общее уравнение плоскости, проходящей через три заданных точки , и .

12. Вычислить длину высоты тетраэдра, опущенной из точки D, если известны его вершины , , и .

13. Вычислить пределы , , , , 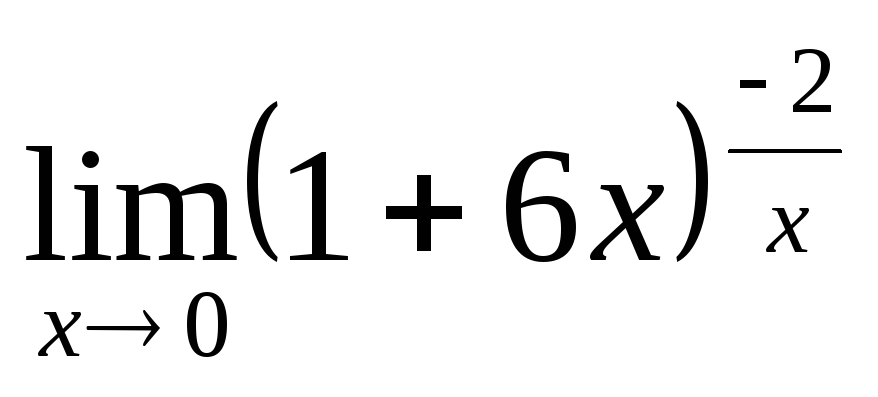. Результаты изобразить на графике.

14. Найти точки разрыва, определить их тип . Изобразить график функции в окрестности точек разрыва.

15. Найти производную функции.

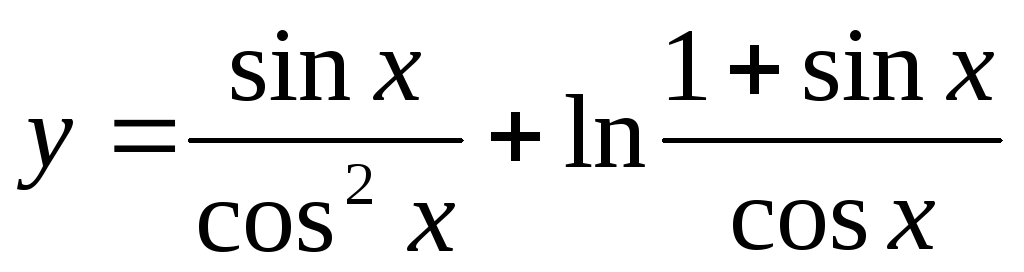16. Найти производную третьего порядка функции .

17. Найти производную первого порядка от функции, заданной параметрически .

18. Найти дифференциал функции .

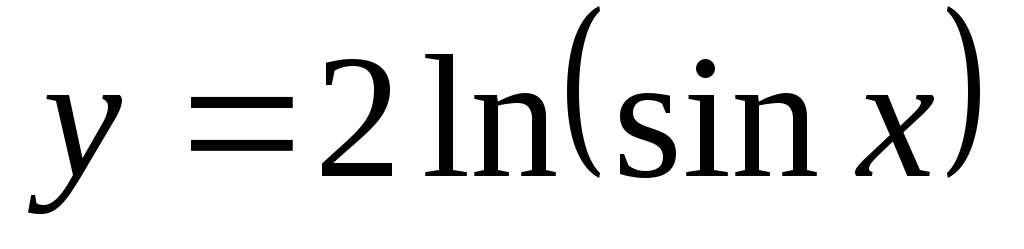19. Используя правило Лопиталя, найти предел . Результат изобразить.

20. На йти асимптоты графика функции . Результат изобразить на графике.

21. Найти точки перегиба графика функции .

22. Построить график функции , проведя полное исследование функции.

23. Найти наибольшее и наименьшее значения функции на отрезке [0,3].

24. Найти расстояние от точки М(0,1.-1) до плоскости 55x-22y-44z+88=0.

25 Найти каноническое уравнение прямой, заданной системой уравнений

11x-66y+55z+99=0, 55x-22y-44z+88=0.

26 Найти общее решение системы уравнений 11x-66y+55z+99=0, 55x-22y-44z+88=0.

27. Найти центр и радиус окружности Изобразить на графике.

28. Вычислить векторное произведение вектора нормали к плоскости 11x +99y –111z-88=0 и

направляющего вектора прямой (x-44)/33=(y-55)/22=(z-66)/77

29. Используя дифференциал, вычислить приближенно f (а+0,001) если известно значение f(a)

(а- заданное число). В частности , .

30 Найти точку пересечения прямой (задача 25) и плоскости x-y+z+9=0.

31. Найти скалярное произведение векторов заданных в

ортонормированном базисе

Пусть матрица оператора в этом базисе. Вычислить .

32. Найти разложение функций и в ряд Маклорена.

Содержание лекций.

1. Аналитическая геометрия с элементами линейной алгебры.

1.1. Геометрические векторы. Вектор. Линейные операции над векторами. Проекция на ось. Декартовы координаты векторов и точек. Скалярное произведение векторов, его основные свойства, координатное выражение. Векторное и смешанное произведение векторов, их основные свойства и геометрический смысл. Определители 2-го и 3-го порядка. Координатное выражение векторного и смешанного произведения.

1.2. Аналитическая геометрия. Прямая на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой. Прямая и плоскость в пространстве. Уравнение плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямыми в пространстве. Угол между прямой и плоскостью. Кривые второго порядка: эллипс, гипербола и парабола. Поверхности второго порядка.

1.3. Системы линейных алгебраических уравнений. Решение системы n линейных алгебраических уравнений методом Гаусса. Определители n-го порядка и их свойства.Разложение определителя по строке (столбцу). Решение системы n линейных алгебраических уравнений с n неизвесными методом Крамера. Матрицы и действия над ними. Обратная матрица. Решение матричных уравнений с помощью обратной матрицы.

1.4. Линейные пространства и операторы. Линейные пространства. Линейно зависимые и линейно независимые вектора. Базис и размерность линейного пространства. Координаты вектора.Линейные операторы и действия над ними. Матрица линейного оператора. Собственные значения и собственные векторы матрицы.

2. Математический анализ.

2.1. Введение в анализ. Функция. Область ее определения. График функции. Сложные и обратные функции. Определение элементарной функции. Основные элементарные функции. Действия над комплексными числами. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числа. Алгебраическая, тригонометрическая и показательная формы комплексного числа. Формула Эйлера. Корни из комплексных чисел.

2.2. Предел и непрерывность функции. Предел функции в точке и на бесконечности. Свойства предела функции. Бесконечно малые и бесконечно большие функции. Односторонние пределы функции. Замечательные пределы. Число e. Сравнение функций. Эквивалентные функции. Непрерывная функция. Непрерывность элементарных функций. Точки разрыва и их классификация.

2.3. Дифференциальное исчисление функции одной переменной. Понятие функции дифференцируемой в точке. Производная функции, её геометрический и физический смысл. Правила дифференцирования. Производная сложной и обратной функций. Таблица производных. Дифференциал функции. Инвариантность формы первого дифференциала. Точки экстремума функции. Теоремы Ферма, Ролля, Лагранжа, Коши. Правила Лопиталя. Производные высших порядков. Формула Тейлора с остаточным членом в форме Пеано и Лагранжа. Разложение основных элементарных функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений. Условия монотонности функции. Необходимые и достаточные условия существования экстремума. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке. Выпуклость графика функции. Точки перегиба. Асимптоты функции. Общая схема исследования функции и построение ее графика.

4.1. ОСНОВНАЯ, ДОПОЛНИТЕЛЬНАЯ И НОРМАТИВНАЯ

ЛИТЕРАТУРА

Основная литература.

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994 (2003).

2. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. М.: Высшая школа, 2000.

3. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 1 : Элементы линейной алгебры и аналитической геометрии. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2004. ‑ 284 с.

4. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 2 : Дифференциальное и интегральное исчисление. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2004. ‑ 509 с.

5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные

интегралы. Ряды. Функции комплексного переменного. - М.: Наука,

1981.

6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и

математической статистике. ‑ М.: Высшая школа, 1998.

7. Пискунов Н.С. Дифференциальное и интегральное исчисление для

ВТУЗов, т.т.1,2 - М.: Наука, 1972-79гг.

8. Сборник задач по математике для втузов. В 4 частях Ч. 1: Учеб. пособие для втузов /А.В. Ефимов, Ф.Ф. Каракулин, И.Б. Кожухов, А.С. Поспелов, А.А. Прокофьев. Под ред. А.В. Ефимова, А.С.Поспелова . ‑ 4-е изд. перераб. и доп. ‑ М.: Физ.-матем. лит., 2003. ‑ 288 с.

5. Сборник задач по математике для втузов. В 4 частях Ч. 2: Учеб. пособие для втузов /А.В. Ефимов, Ф.Ф. Каракулин, И.Б. Кожухов, А.С. Поспелов, А.А. Прокофьев. Под ред. А.В. Ефимова, А.С.Поспелова . ‑ 4-е изд. перераб. и доп. ‑ М.: Физ.-матем. лит., 2003. ‑ 288 с.

6. Сборник задач по математике для втузов: В 4 частях Ч. 3: Учеб. пособие для втузов /Э.А. Вуколов, А.В. Ефимов, В.Н. Земков, А.С. Поспелов. Под ред. А.В.Ефимова, А.С.Поспелова . ‑ 3-е изд. перераб. и доп. ‑ М.: Физ.-матем. лит., 2004. ‑ 432 с.

7. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для

инженера. ‑ М.: Энергоатомиздат, 1988.

12.Вентцель А.Д., Овчаров Л.А. Теория вероятностей и ее инженерные приложения.: Учеб. пособие - 2-е изд., стер. - М.: Высшая школа, 2000. – 480 с.

Дополнительная литература

13. Фихтенгольц Г.М. Основы математического анализа. В 2-х томах. Т.1. –

СПб.: Издательство «Лань», 2001. – 448 с.

14. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах.

часть 1,2. - М.: Высшая школа, 1974.

3