Счетчик Джонсона.
Счетчик Джонсона.. Так часто называют кольцевой счетчик, который тоже строится на основе замкнутого регистра сдвига, но с одной перекрестной (инверсной) связью. На рис. 6 показана схема построенного таким путем счетчика, имеющего коэффициент пересчета 10.
Рисунок 6. Схема счетчика Джонсона.
Здесь регистр сдвига К155ИР1 дополнен D-триггером. Вход D-триггера соединен с выходом четвертого разряда регистра, а на информационный вход I регистра подан сигнал не с прямого, а с инверсного выхода этого триггера. За счет этого и реализуется перекрестная связь в кольце. В отличие от простейших кольцевых счетчиков счетчик Джонсона имеет коэффициент пересчета вдвое больший числа составляющих его триггеров. В частности, счетчик рис. 6 под воздействием счетных импульсов n последовательно проходит следующие состояния:
|
n |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
2 |
1 |
1 |
0 |
0 |
0 |
|
3 |
1 |
1 |
1 |
0 |
0 |
|
4 |
1 |
1 |
1 |
1 |
0 |
|
5 |
1 |
1 |
1 |
1 |
1 |
|
6 |
0 |
1 |
1 |
1 |
1 |
|
7 |
0 |
0 |
1 |
1 |
1 |
|
8 |
0 |
0 |
0 |
1 |
1 |
|
9 |
0 |
0 |
0 |
0 |
1 |
Как видно, при счете сначала от первого разряда до последнего распространяется волна единиц, а затем волна нулей. В счетчике Джонсона, как и в других кольцевых счетчиках, возможны сбои в виде лишних волн нулей или единиц. Для предотвращения их в десятичном счетчике простая цепь связи инверсного выхода последнего и входа первого разряда I=Q5 может быть заменена логической ячейкой, реализующей функцию I=Q1Q4+Q5. Связи, соответствующие этой ячейке, показаны штриховыми линиями на рис. 6. Подобная ячейка обеспечивает переход счетчика под воздействием входных импульсов из любой запрещенной комбинации в одну из разрешенных. На основе регистра с одной перекрестной связью может быть построен счетчик с любым четным коэффициентом пересчета. Если же нужен нечетный коэффициент пересчета 2N-1, то используется N-разрядный регистр сдвига, но на вход 1-го разряда подается сигнал неQN, a QNQN-i. При этом по сравнению с обычным счетчиком Джонсона пропускается одна кодовая комбинация, полностью составленная из нулей.
Двоичные счетчики.
Счётчики используются для построения таймеров или для выборки инструкций из ПЗУ в микропроцессорах. Они могут использоваться как делители частоты в управляемых генераторах частоты (синтезаторах). При использовании в цепи ФАП счётчики могут быть использованы для умножения частоты как в синтезаторах, так и в микропроцессорах.
Двоичные асинхронные счётчики
Простейший вид счётчика - двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 1.
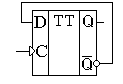
Рисунок 1 Реализация счетного T-триггера на универсальном D-триггере.
Так как эта схема, как мы уже рассматривали ранее, при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 2.
Рисунок 2 Временные диаграммы сигналов на входе и выходах T-триггера.
Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два.
Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчика Q0 … Q3. Это число будет представлено в двоичном коде.
Рисунок 3 Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах.
Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 4.
Рисунок 4 Временная диаграмма четырёхразрядного счётчика.
Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу.
Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах.
Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 4. Запишем новое состояние выходов счётчика в таблицу 1. В этой строке таблицы образовалось двоичное число 2. Оно совпадает с номером входного импульса.
Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.