26. Проектирование автомата. Определение функций выхода.
Данная функция определяется из закодированной таблицы выходов:
|
g |
000 |
001 |
010 |
100 |
011 |
111 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
000 |
0 |
0 |
0 |
0 |
1 |
1 |
|
001 |
1 |
0 |
1 |
1 |
1 |
0 |
|
010 |
0 |
0 |
0 |
0 |
1 |
0 |
|
100 |
0 |
0 |
1 |
0 |
0 |
0 |
|
011 |
0 |
0 |
0 |
0 |
0 |
0 |
Функция выхода определяется из кодированной таблицы выходов по следующей методике: если обозначить кодирующие переменные входа как а1, а2 и а3, состояний – как t1 , t2, t3, выхода – какg, то функция выхода будет иметь вид:
27. Минимизация логических функций методом Квайна и картами Карно.
Минимизация логический функций позволяет нам уменьшить функции возбуждения триггеров, полученные при проектировании. Это даёт нам возможность составить более удобную схему автомата, с наименьшим количеством составляющих.
В своей курсовой я пользовался двумя методами минимизации – методом Квайна и картами Карно.
Одна и та же функция, минимизированная каждым методом будет одинакова, но разница в удобстве использования каждого метода, в зависимости от рассматриваемой функции.
К примеру функцию
Удобно минимизировать с помощью карт Карно, т.к. функция не большая и много внимания её не требуется.
Карта Карно для этой функции будет выглядеть следующим образом:
|
|
|
| |||||||
|
|
0 |
0 |
0 |
0 |
| ||||
|
0 |
0 |
0 |
0 |
| |||||
|
|
1 |
0 |
0 |
1 | |||||
|
1 |
0 |
1 |
0 |
| |||||
|
|
|
|
| ||||||
Для её составления я записываю все буквы из функции по краям карты так, чтобы каждая пересекалась с каждой. Затем в нужных точках мы ставим единицы, это те пересечения, которые присутствуют в функции, нулями те – которых нет. Суть карт в том, что если две единицы находятся рядом, то эти слова из формулы мы объединяем.
Объединив мы получим такую упрощённую функцию:
А теперь рассмотрим функцию
Все слова которой, на картах Карно показать проблематично. Именно для таких функций мы и используем метод Квайна.
Он заключается в том, что мы составляем таблицу, в первой строке которой мы записываем все слова из этой функции, а в первом столбце все, кроме несокращаемых. После чего заполняем «Х» пересечения, где слово из столбца полностью войдёт в слово из строки, всё это очень сложно объяснить, но выглядит оно следующим образом:
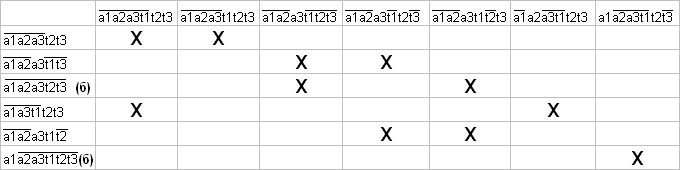
Вначале мы выделяем базовые состояния в столбце и сразу же сокращаем в строках соответствующие им слова. Затем смотрим, какие ещё не сокращены и пытаемся выбрать способ, чтобы при наименьшем количестве используемых слов в столбце, сократить все слова в столбце.
После чего те которые были задействованы, записываем в функцию возбуждения:
28. Синтез логических схем. Понятие базиса.
Любая логическая схема без памяти полностью описывается таблицей истинности. Эта таблица является исходной информацией для синтеза схемы на основе логических элементов «И», «ИЛИ», «НЕ». Для разработки требуемого цифрового устройства сначала на основе таблицы истинности записывают его логическое выражение. Затем с целью упрощения цифрового устройства минимизируют его логическое выражение и далее разрабатывают схему, реализующую полученное логическое выражение. Логические выражения можно получить двумя способами:
на основе совершенной дизъюнктивной нормальной формы (СДНФ)
на основе совершенной конъюнктивной нормальной формы (СКНФ)
Совершенная дизъюнктивная нормальная форма (СДНФ)
Функция представляется суммой групп. Каждая группа состоит из произведения, в которую входят все переменные.
f(х)=x1·x2·x3 + x1·x2·x3 + x1·x2·x3
Совершенная конъюнктивная нормальная форма (СКНФ)
Функция представляется произведением групп. Каждая группа состоит из суммы, в которую входят все переменные.
f(х)=(x1+x2+x3) · (x1+x2+x3) · (x1+x2+x3)
Если схема имеет несколько выходов, то каждый выход описывается своей функцией. Такая система функций называется системой собственных функций. СДНФ составляется на основе таблицы истинности по следующему правилу: для каждого набора переменных, при котором функция равна 1, записывается произведение, в котором с отрицанием берутся переменные, имеющие значение «0».