высшая матеметика(часть 1)
.doc1. дифференциальные уравнения первого порядка
А)Уравнения с разделяющимеся переменными
1)
умножим на dx
разделим на tgy
2)
умножим на dx
разделим на 
разделим на 
Ответ: 
3)
разделим на x
разделим на 
4)
умножим на 
разделим на 
разделим на 
Ответ: 
5)
разделим на 
разделим на 
Ответ: 
6)
разделим на 
умножим на 
Ответ: 
7)
разделим на 
разделим на 
=
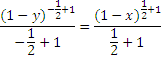
Ответ: 
Б)линейные уравнения
1)
Воспользуемся подстановкой Бернулли:
сгруппируем члены в левой части
равенства, определим функцию 
так, чтобы коэффициент при 
обращался в ноль,т.е.
б)
разделим на 
разделим на 
Проинтегрируем это уравнение:
Ответ: 
2)
Воспользуемся подстановкой Бернулли:
сгруппируем члены в левой части
равенства, определим функцию 
так, чтобы коэффициент при 
обращался в ноль.
а)
разделим на 
Проинтегрируем это уравнение:
б)
умножим на 
разделим на 
Проинтегрируем это уравнение:
Ответ: 
3)
Воспользуемся подстановкой Бернулли:
сгруппируем члены в левой части равенства,
определим функцию 
так, чтобы коэффициент при 
обращался в ноль.
а)
умножим на 
разделим на 
разделим на 
Проинтегрируем это уравнение:
б)
умножим на 
разделим на 
Проинтегрируем это уравнение:
Ответ: 
4)
Воспользуемся подстановкой Бернулли:
сгруппируем члены в левой части равенства,
определим функцию 
так, чтобы коэффициент при 
обращался в ноль.
а)
умножим на 
разделим на 
разделим на 
Проинтегрируем это уравнение:
б) 
умножим на 
разделим на 
Проинтегрируем это уравнение:
Ответ: 
2) дифференциальные уравнения второго порядка
А.линейные дифференциальные уравнения второго порядка со специальной правой частью.
1)
Подбираем частное решение в виде правой части:
Подставим его в уравнение:
сократим на 
-частное
решение
Общее решение соответствует однородному уравнению
Составим характеристическое уравнение:
a)
б)
-решение однородного уравнения
Общее решение данного уравнения имеет вид:
Ответ: 
2)
Подбираем частное решение в виде правой части:
Подставим его в уравнение:
сократим на 
-частное решение
Общее решение соответствует однородному уравнению
Составим характеристическое уравнение:
-решение однородного уравнения
Общее решение данного уравнения имеет вид:
Ответ: 
3)
Подбираем частное решение в виде правой части:
