
Математика. Задачи к экзамену
..docЗадачи к экзамену по математике
для студентов 1 курса ФМА
1 семестр
Раздел 1: линейная алгебра.
Задача 1.
-
Найти 5A – 3B + 2C,

-
Найти 3A + 2B - 4C,

-
Найти A – 12E,

-
Найти 4A – 7B,

-
Найти 5A – 4B,
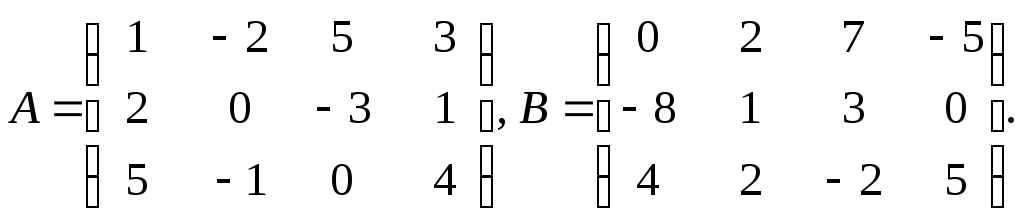
-
Найти значение матричного многочлена f(A):
 .
. -
Найти значение матричного многочлена f(A):
 .
.
Задача 2. Вычислить определитель матрицы:
1.А= 2.
2.
 3.
3.
 4.
4.
 5.
5.
 .
.
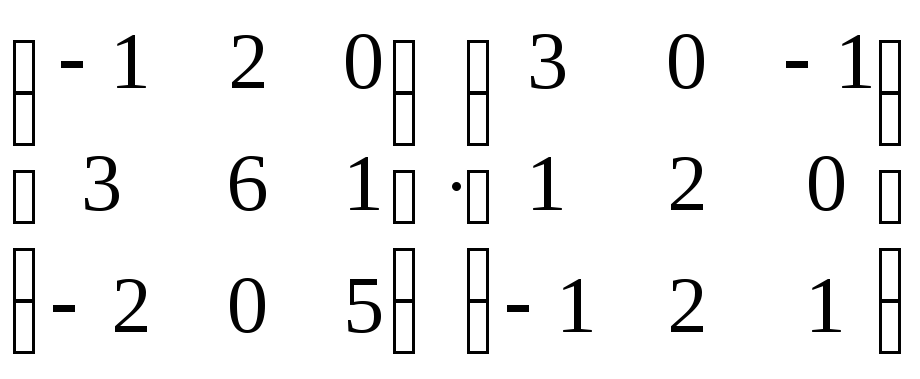
Задача 3. Найти произведение матриц:
1.
![]() 2.
2.
![]() 3.
3.
 .
.
Задача 4. Вычислить обратную матрицу:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
 .
.
Раздел 2: векторная алгебра.
Задача 1. Написать разложение вектора
![]() по векторам
по векторам
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 2. Коллинеарны ли векторы
![]() и
и
![]() ,
построенные по векторам
,
построенные по векторам
![]() и
и
![]() ?
?
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 3. Найти косинус угла между
векторами
![]() и
и
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 4. Вычислить площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 5. Компланарны ли векторы
![]() ,
,
![]() и
и
![]() ?
?
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 6. Вычислить объем тетраэдра
с вершинами в точках
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Раздел 3: аналитическая геометрия в пространстве.
Задача 1. Найти расстояние от точки
![]() до плоскости, проходящей через точки
до плоскости, проходящей через точки
![]() .
.
1.![]()
2.
![]()
3.![]()
4.
![]()
5.
![]()
Задача 2. Написать уравнение плоскости,
проходящей через точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 3. Написать канонические уравнения прямой.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Задача 4. Найти точку пересечения прямой и плоскости.
1.

2.

3.

4.

5.
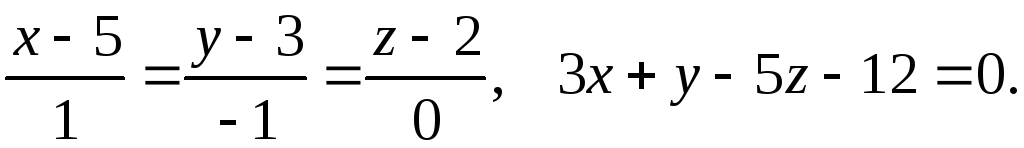
Раздел 4: аналитическая геометрия на плоскости.
1. Составить уравнение прямой, проходящей через точки А(1,-3) и В(2,-1).
2. Составить уравнение прямой, проходящей через точки А(1,3) и В(2,2).
3.Определить площадь треугольника, образованного прямой y = - 0,5x + 2 с осями координат
4. В треугольнике АВС, где т. А(4,-1), т. В(2,3), т. С(-4,-3), написать уравнение медианы, проведенной из т. А.
5. В треугольнике АВС, где т. А(-13,3), т. В(-1,-2), т. С(2,2), написать уравнение высоты проведённой из точки А.
6. В треугольнике АВС, где т. А(0,4), т. В(2,-6), т. С(-4,2), написать уравнение средней линии, параллельной ВС.
7. Найти точку пересечения диагоналей четырёхугольника АВСД, если А(0,6),В(7,12),С(6,2), Д(2,2).
8. Даны вершины треугольника АВС: А(-3, 1), В(0, 4), С(2, 5). Написать уравнение высоты, проведенной из вершины С к стороне АВ.
9. Стороны треугольника АВС заданы уравнениями: x+y=2 (AB), 2x-y=-2 (AC), x-2y=2 (BC).
Написать уравнение высоты, проведенной из вершины А к стороне ВС.
10. Даны вершины треугольника АВС: А(4, -2), В(3, -1), С(2, 6). Написать уравнение средней линии ΔАВС, параллельной стороне АС.
11. Стороны треугольника АВС заданы уравнениями:x+y-3=0 (AB), y-2x=0 (AC), x-y-1=0 (BC).
Написать уравнение прямой, проходящей через вершину А параллельно стороне ВС.
12. Даны вершины четырехугольника A(0, 6), B(7,12), C(6, 2), D(2, 2). Найти точку пересечения его диагоналей.
13. Даны вершины треугольника АВС: А(0, 4), В(-3, 2), С(2, 6). Написать уравнение медианы, проведенной из точки В.
14. Даны вершины треугольника АВС: А(2, 4), В(-2, 5), С(-1, 2). Написать уравнение высоты, проведенной из вершины А к стороне ВС.
15. Даны вершины трапеции A(-2,-3), B(-3, 1), C(7, 7), D(3, 0). Написать уравнение средней линии трапеции.
16. В треугольнике MNP написать уравнение медианы, проведенной из вершины М, если известно, что М(4, -1), N(2, 3), P(-4, -2).
17. Стороны треугольника лежат на прямых:x-y=-2 (AB), x+y=1 (BC), x-2y=1 (AC).
Написать уравнение высоты, опущенной из вершины В на сторону АС.
Раздел 5. Пределы. Непрерывность функции.
Вычислить пределы функций, не пользуясь средствами дифференциального исчисления
1. 1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]()
6.![]() 7.
7.![]() 8.
8.![]() 9.
9.![]() 10.
10.![]()
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.
![]()
![]()
2. 16.![]() 17.
17.![]() 18.
18.![]() 19.
19.![]()
20.![]() 21.
21.![]() 22.
22.![]() 23.
23.![]()
24.![]() 25.
25.![]() 26.
26.![]() 27.
27.![]()
28.![]() 29.
29.![]() 30.
30.![]()
31.![]() 32.
32.![]() 33.
33.![]() 34.
34.![]()
3. 35.![]() 36.
36.![]() 37.
37.![]() 38.
38.![]() 39.
39.![]()
40.![]() 41.
41.![]() 42.
42.![]() 43.
43. 44.
44.![]()
45.![]() 46.
46.![]()
4. 47.![]() 48.
48.![]() 49.
49.![]() 50.
50.![]()
51.![]() 52.
52.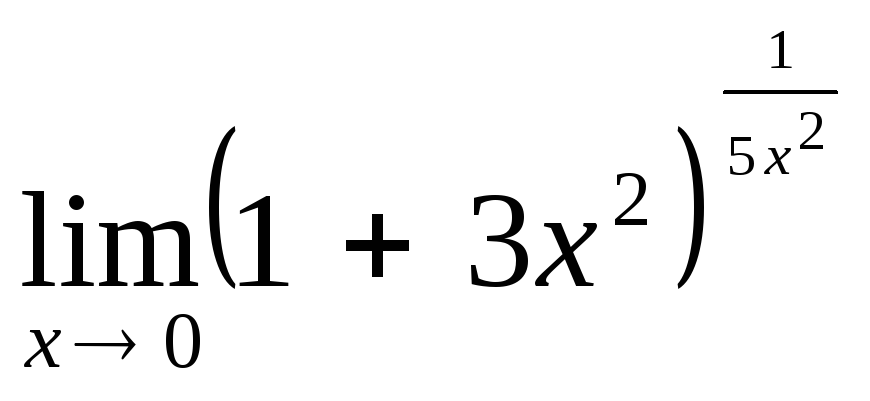 53.
53.![]() 54.
54.![]()
55.![]() 56.
56.![]() 57.
57.![]() 58.
58.![]() 59.
59.![]()
5. 60.![]() 61.
61.![]() 62.
62.![]()
63![]()
64.![]() 65.
65.![]() 66.
66.![]() 67.
67.![]()
68.![]() 69.
69.![]()
70.![]()
6. Найти точки разрыва функции и установить характер разрыва.
1. у = 2. у =
2. у = 3.
у =
3.
у =
4. у = 5.
у =
5.
у =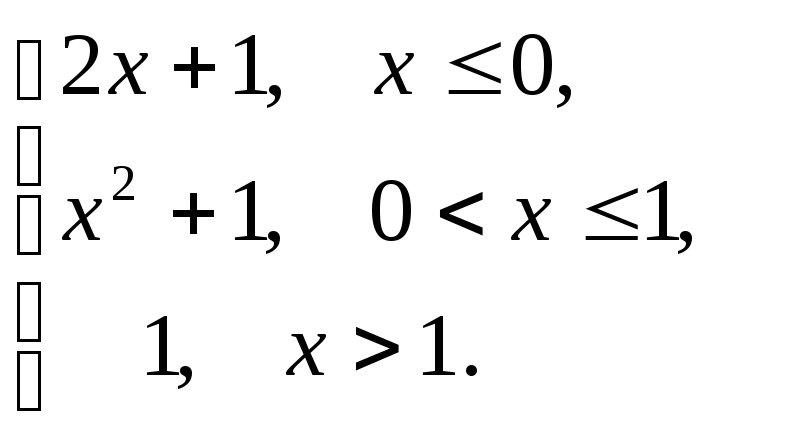
Раздел 6. Вычислить производные следующих функций:
А. 1.a)
![]() b)
b)
![]() c)
c)
![]()
2. a)
![]() b)
b)
![]() c)
c)
![]()
3. a)
![]() b)
b)
![]() c)
c)
![]()
4. a)
![]() b)
b)
![]() c)
c)
![]()
5. a)
![]() b)
b)
![]() c)
c)
![]()
6. a)
![]() b)
b)
![]() c)
c)
![]()
7. a)
![]() b)
b)
![]() c)
c)
![]()
8. a)
![]() b)
b)
![]() c)
c)
![]()
9. a)
![]() b)
b)
![]() c)
c)
![]()
10. a)
![]() b)
b)
![]() c)
c)
![]()
В. 1)![]() 2)
2)
![]() 3)
3)![]() 4)
4)
![]()
5)![]() 6)
6)
![]() 7)
7)![]() 8)
8)![]() 9)
9)
![]()
10)![]() 11)
11)![]() 12)
12)![]() 13)
13)![]()
14)![]() 15)
15)
![]() 16)
16)
![]()
17)![]() 18)
18)![]() 19)
19)![]() 20)
20)![]() 21)
21)![]() 22)
22)![]() 23)
23)![]() 24)
24)![]() 25)
25)
![]()
26)![]() 27)
27)
![]() 28)
28)![]()
29)![]() 30)
30)![]() 31)
31)
![]() 32)
32)
![]()
33)
![]() 34)
34)
![]() 35)
35)
![]()
36) 1)![]() ,
37)
,
37)
![]() ,
38)
,
38)
![]() ,
39)
,
39)
![]() ,
40)
,
40)
![]() ,
,
41)
![]() ,
42)
,
42)
![]() ,
43)
,
43)
![]() ,
44)
,
44)
![]() ,
,
45)
![]() ,
46)
,
46)
![]() ,
47)
,
47)
![]() ,
48)
,
48)
![]() ,
,
49)
![]() ,
50)
,
50)
![]() ,
51)
,
51)
![]() ,
52)
,
52)
![]() ,
,
53)
![]() ,
54)
,
54)
![]() ,
55)
,
55)
![]() .
.
С. 1)![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5)![]() 6)
6)![]() 7)
7)![]() 8)
8)
![]()
9)
![]() 10)
10)
![]() 11)
11)
![]() 12)
12)
![]() 13)
13)
![]()
13)
![]() ,
14)
,
14)![]() ,
15)
,
15)![]() ,
16)
,
16)![]() .
.
D. Найти производную параметрически заданной функции:
1)x=t-sint, y=2-cost; 2) x=e-t, y=arcsint; 3) x=sint+cost, y=sin2t;
4)x=tg2t, y=cos2t; 5) x=sint, y=ln(cost); 6) x=etsint, y=t+sint
7)
 8)
8)
 9)
9)
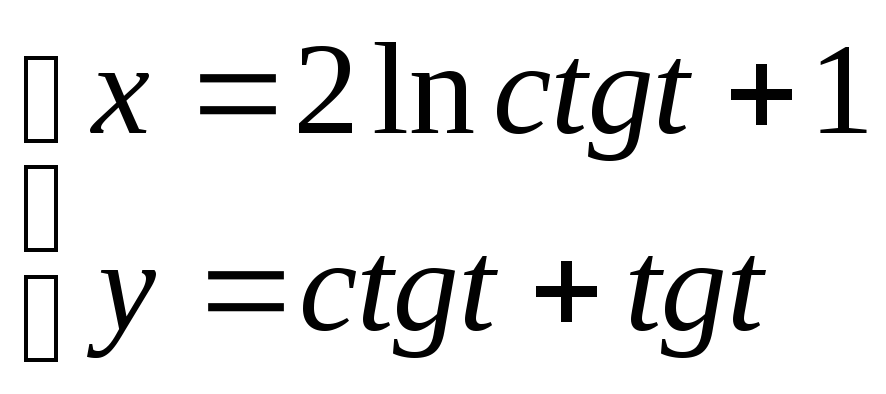 10)
10)

11)

