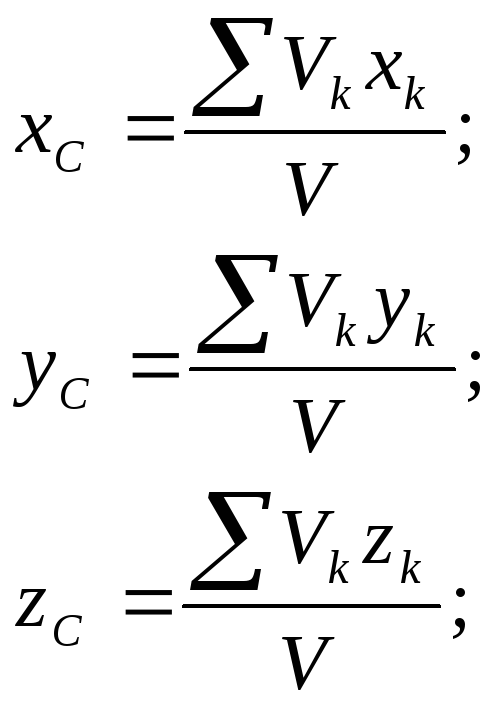1.15 Центр тяжести тел и методы определения его координат

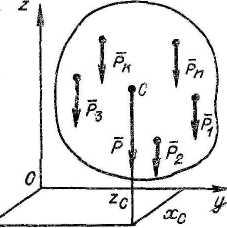
Силы тяжести частей тела с некоторым допущением можно считать параллельными, а их совокупность принимать за систему параллельных сил тяжести, эквива­лентную равнодействующей , называемой силой тяжести тела

Сила тяжести тела проходит через т. C - центр параллель­ных сил тяжести, или центр тяжести (ЦТ) тела, который не меняет своего положения относительно тела при любом положении тела в простран­стве.

Координаты центра тяжести тела

Центры тяжести однородных тел зависят только от их геометрической формы, поэтому формулы (1) можно записать в виде

ЦТ объема	ЦТ площади	ЦТ линии	(2)

V_k, S_k, L_k - объемы, площади, длины частей тела; V, S, L - объем, площадь, длина всего тела; суммы в числителях - статические моменты объема, площади, линии.

1). Центры тяжести симметричных однородных тел

Если тело имеет плоскость, ось или центр симметрии, то центр тя­жести этого тела находится соот­ветственно на плоскости, оси или в центре симметрии.

2). Метод разбиения

Разбиение на части с известными центрами тяжести
Хc =0; Нc =8,75 см.	Часть 1 2 3 Sk, см2 14 30 27 xk, см 0 0 0 yk, см 19 10,5 1,5

Если в теле есть вырезанные части, то их объемы (площади) принимаются отрицательными
	Часть 1 2 Sk, см2 160 -24 xk, см 10 18 yk, см 0 0	xс =14,9 см; ус = 0.

3). Интегрирование

В этом случае разбиения тела суммы, стоящие в чис­лителях формул координат центра тяжести, обращаются в интегралы с пределами интегрирования по всему объему (площади, линии) тела

Пример

Определить положение центра тяжести конуса.
	Выделим элемент конуса высотой объемом.найдем по формуле где . В результате получим .

4). Экспериментальные методы (для неоднородных тел сложной формы)

3.1 Метод взвешивания
	; .
3.2. Метод уравновешивания
		Двигая тело вправо-влево, обеспечивают его равновесие на призме. Центр тяжести тела нахо­дится на вертикали, проходящей через призму.

1. 16 Условия равновесия тел при его опрокидывании

Силы, приложенные к свободностоящему телу, могут привести к его опрокидыванию.

Покажем на примере, как получить условия неопро­кидывания тела, рассмотрим прямоугольный параллелепипед (весом G), свободностоящий на горизонтальной шероховатой плоскости (коэффициент трения f). Найдем условия неопрокидывания параллелепипеда под дейст­вием силы р (см. Рисунок).

В предельном положении равновесия тела (положе­нии, предшествующем его опрокидыванию, когда реакция шероховатой поверхности приложена в т. A)

; ; .

Тогда условия неопроки­дывания примут вид:

а) по величине силы

;

б) по величине плеча

;

в) по углу, составляемому равнодействующей сил P и G с вертикалью

;

г) в общем случае произвольной системы сил

,

M_уд - удерживающий момент;

M_опр - опрокидывающий момент;

K - коэффициент устойчивости.

Пример

Проверить устойчивость кра­на, если вес поднимаемого груза G_г, вес крана G_к, вес противовеса G_п, ветровая нагрузка P_в. Коэффициент устойчивости должен быть не менее k = 1,25. Груз поднима­ется равномерно. На рисунке раз­меры - в метрах. G_г = 50 кН; G_к = 600 кН; G_п = 25 кН; P_в = 12 кН.

1. Кран без груза

Опрокидывание возможно вокруг т. A. В положении предельного равновесия реакция R_в = 0. Направление ветра вправо:

;

;

k = 14,0 - кран устойчив.

Направление ветра влево:

;

;

2. Кран с грузом

Опрокидывайие возможно вокруг точки B. В положении предельного равновесия реакции R_A = 0. Направление вет­ра вправо:

;

;

k = 0,63 - кран неустойчив.

Вывод: при ветре кран к эксплуатации непригоден.

19