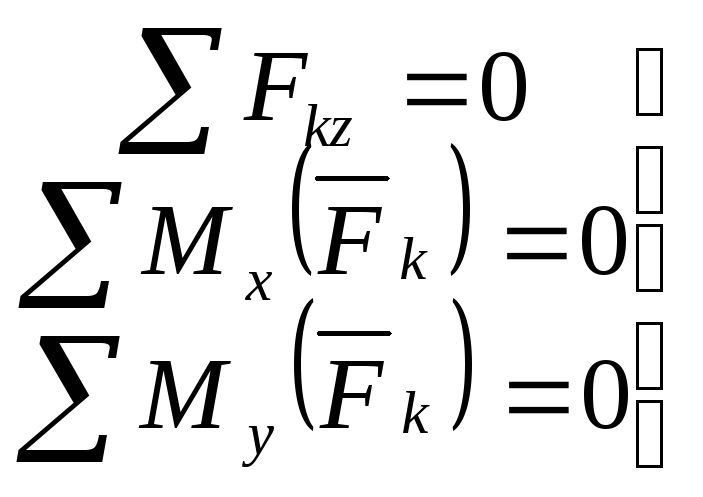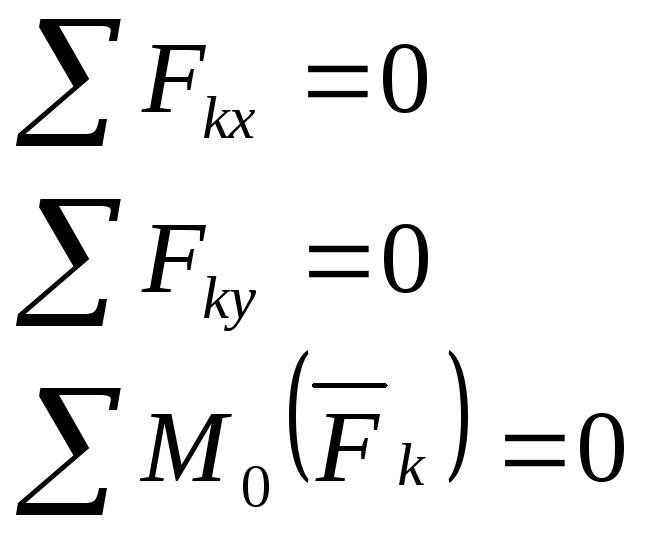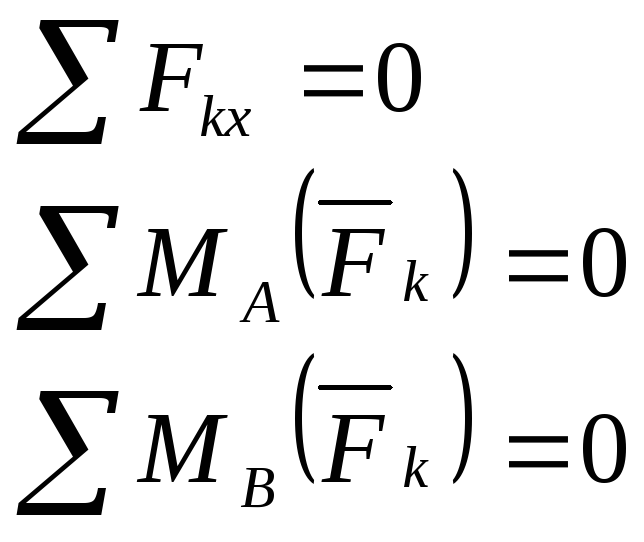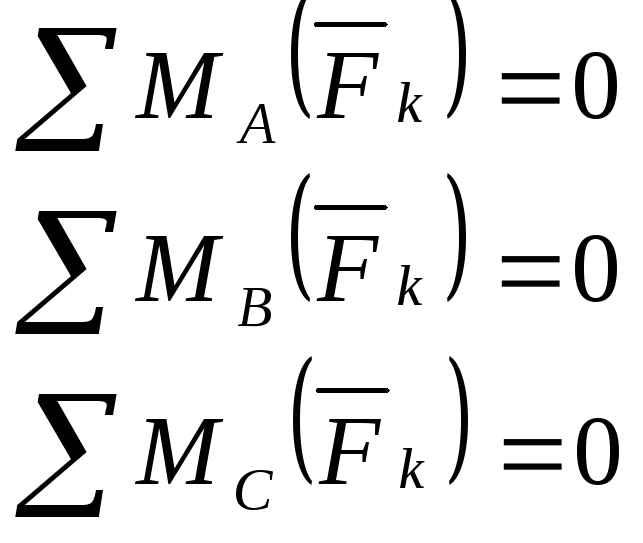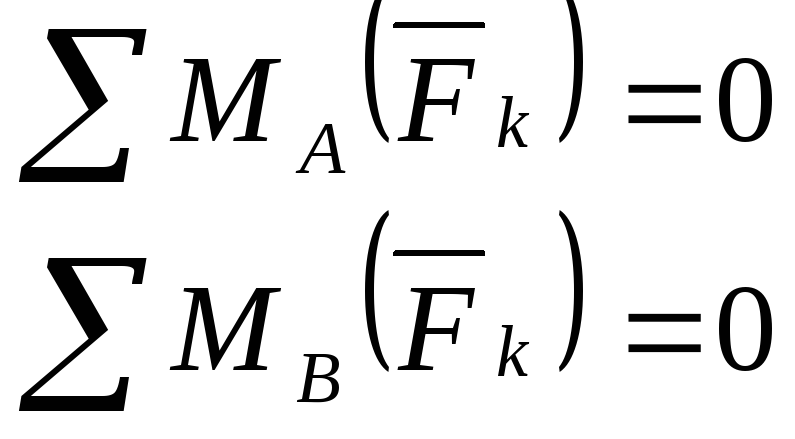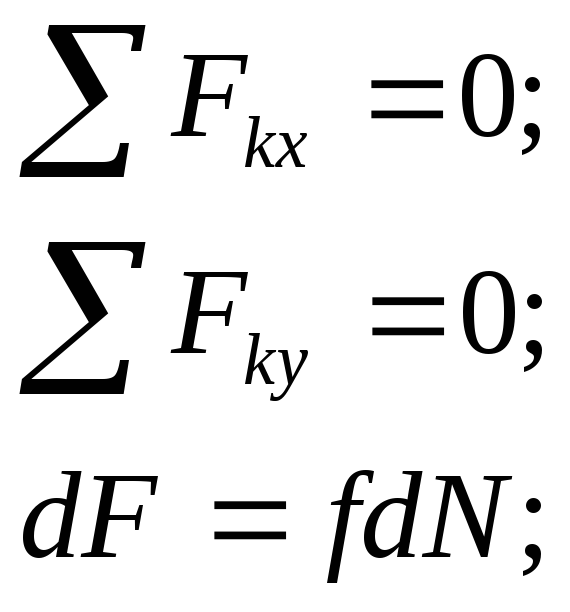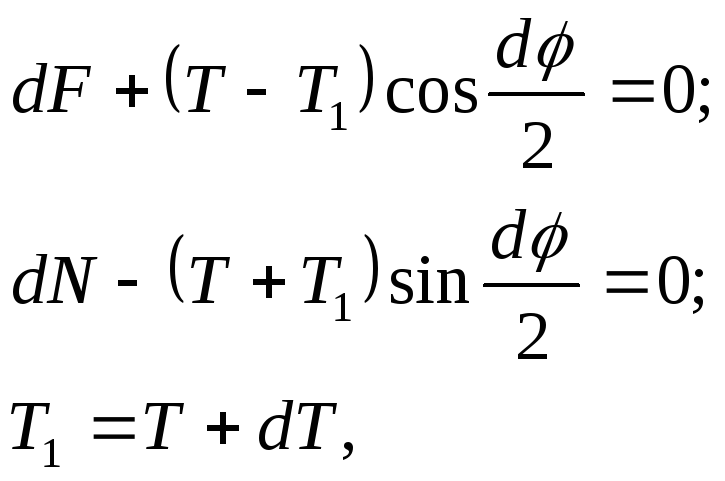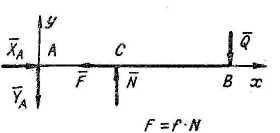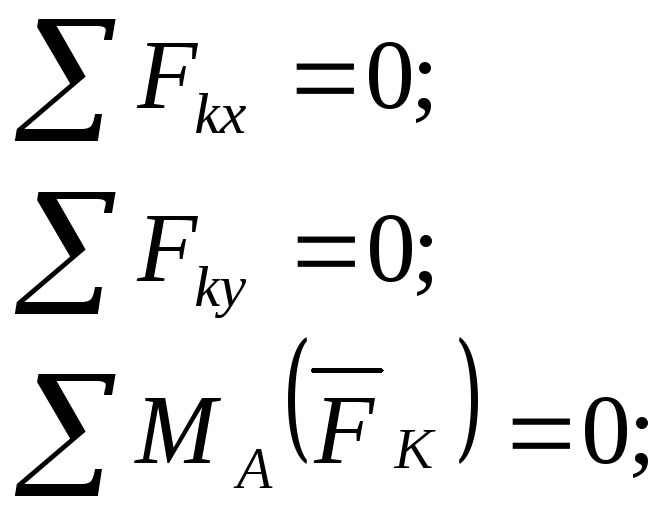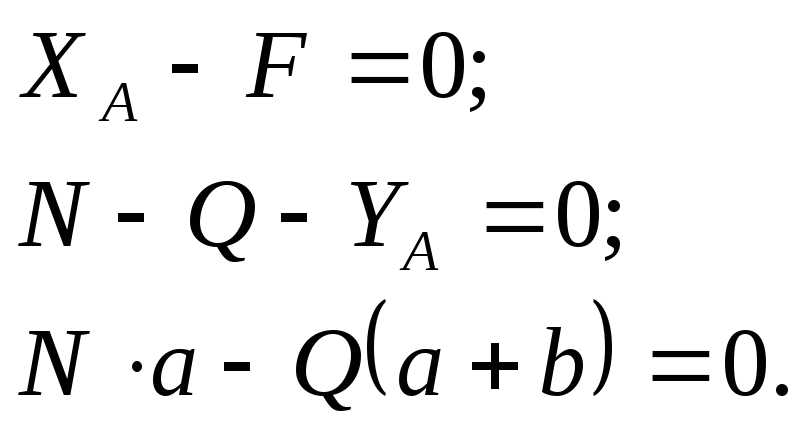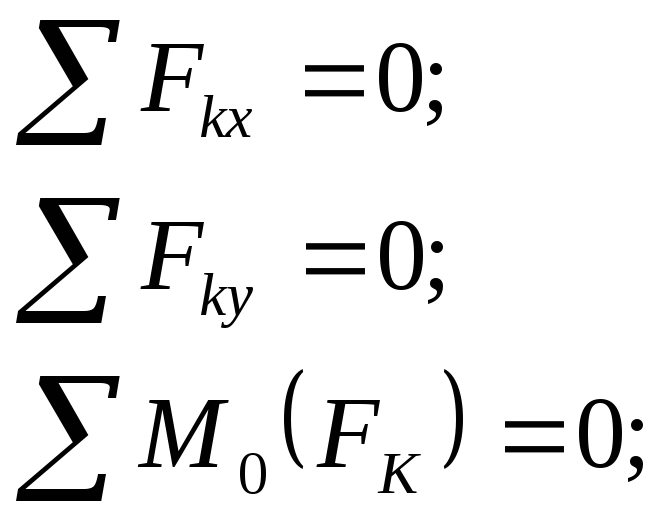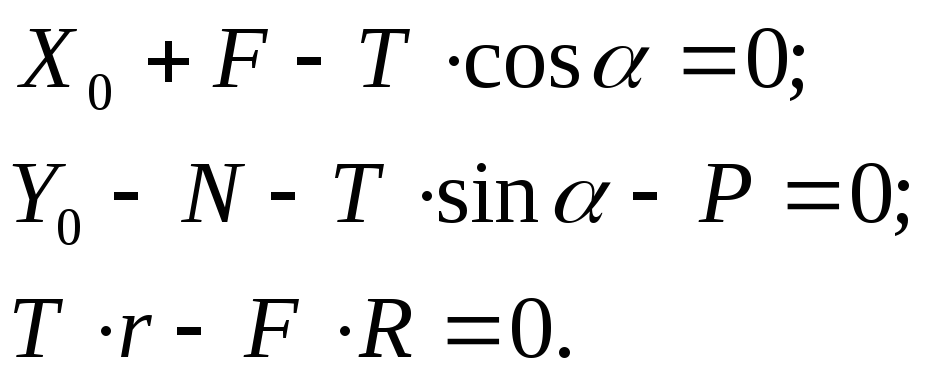Примеры эквивалентной замены сил

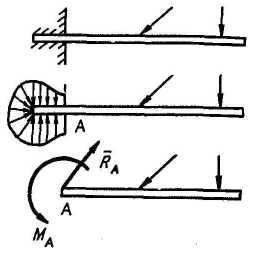
1. реакция жесткой заделки. балка AB, один конец которой заделан в стену, находится под действием плоской системы сил. Распределенные силы реакции со стороны стены можно заменить одной силой и одной парой сил с моментом

.

1.11 Условия равновесия произвольной пространственной системы сил

	условия равновесия произвольной пространственной системы сил
	условия равновесия системы параллельных сил (силы параллельных оси z)

1.12 Условия равновесия произвольной плоской системы сил

Для плоской системы сил

Откуда получаются условия равновесия в форме 1. Условия равновесия могут быть выражены и другими равенствами (форма 2 и форма 3).

Условия равновесия плоской системы сил

Форма 1	Форма 2	Форма 3
	ось x	Точки A, B, C – не на одной прямой

Условия равновесия системы параллельных сил

Если силы парал­лельны оси Y, то

Форма 1

Форма 2 AB не ║ оси y

1.13 Равновесие тел с учетом трения

Согласно законам кулона, сила трения может изме­няться в пределах , - предельная сила трения.

При анализе равновесия тел с учетом трения обыч­но рассматривается предельное состояние, при кото­ром , - коэффициент статического трения;N - нормальная реакция поверхности.

Примеры

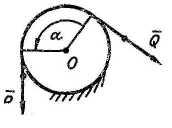
1). Трение невесомого троса о цилиндрическую поверхность.

определить соотношение между сила­ми и, приложенными к концам троса, огибающего неподвижную шерохо­ватую цилиндрическую поверхность, в случае равновесия троса.

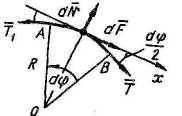
Задача решается при условии предельного равновесия троса. Рассмотрим равновесие элемента AB троса длиной . Расчетная схема условия и уравнения равновесия:

и -силы натяжения на концах элемента AB; , - рав­нодействующие сил трения и нормальных реакций. Полагая и пренебрегая членами, содержащими малые высшего порядка, находим

Интегрируя это уравнение, получим

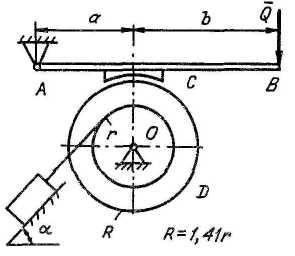
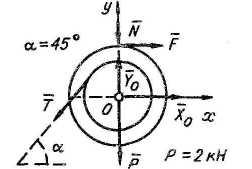
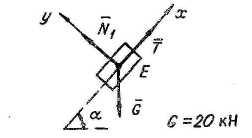
2). Расчет тормозного устройства

Определить минимальное значение силы Q и реакции опор O и A. Весом рычага AB, колодки С и нити пренебречь. Трение в опорах, а также между телом и наклон­ной плоскостью пренебрежимо мало. Коэффициент трения меж­ду колодкой и шкивом равен f = 0,2; размеры а = 0,1 м; b = 0,15 м. Минимальное значе­ние силы соответствует пре­дельному состоянию равнове­сия системы тел.

Расчетные схемы и уравнения:

Решая систему полученных уравнений равновесия, находим

= 20 кН; = 10 кН;= 30 кН; = 0; = 62 кН.

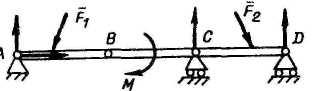
1.14 Равновесие системы тел

Рассмотрим равновесие двух тел. Соединенных шар­ниром ( в точке B ).

Неизвестных реакций – 4 уравнений равновесия для системы в целом - 3

Но эта задача не является статически неопределимой, так как, расчленив систему и составив уравнения равно­весия для каждой части, можно замкнуть задачу: приве­сти в соответствие количество неизвестных и число уравнений:

Согласно аксиоме «о действии и противодействии»,

Итого: 6 неизвестных и 6 уравнений равновесия (3+3). Для системы трех тел имеем ( шарниры в точках A и C ):