- •Теоретическая механика
- •1 Основные положения раздела "статика"
- •1.1 Силы и системы сил
- •1.2 Основные определения
- •Распределенная нагрузка
- •1. 3 Основные сведения о векторах
- •1.4 Аксиомы статики
- •Теорема Вариньона
- •1. 6 Пара сил и ее свойства
- •1. 7 Связи и их реакции
- •1.8 Система сходящихся сил
- •1. 9 Система пар сил
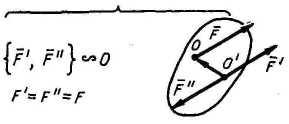
- •1. 10 Основная теорема статики (метод Пуансо)
- •Примеры эквивалентной замены сил
- •1.11 Условия равновесия произвольной пространственной системы сил
- •1.12 Условия равновесия произвольной плоской системы сил
- •1.13 Равновесие тел с учетом трения
- •1.14 Равновесие системы тел
- •1.15 Центр тяжести тел и методы определения его координат
- •1). Центры тяжести симметричных однородных тел
- •2). Метод разбиения
- •3). Интегрирование
- •4). Экспериментальные методы (для неоднородных тел сложной формы)
- •1. 16 Условия равновесия тел при его опрокидывании
1. 7 Связи и их реакции
|
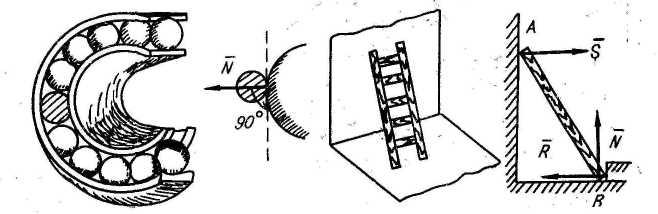
1. Опорная гладкая поверхность |
| |
|
|
| |
|
Реакция направляется перпендикулярно опорной или опирающейся поверхности |
| |
|
2. Невесомая гибкая связь (нить. Трос, цепь) | ||
|
|
Реакция невесомой гибкой нити направляется вдоль этой нити от тела.
| |
|
3. Цилиндрический шарнир и катковая опора |
|
|
|
Реакции направляются по нормали к поверхности качения (катковые опоры B, C, D); в цилиндрическом шарнире A возникают две составляющие реакции |
|
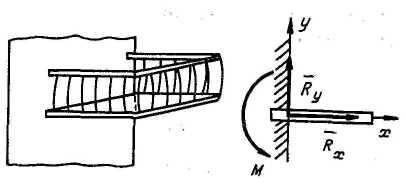
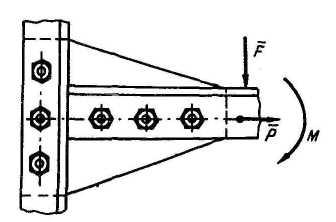
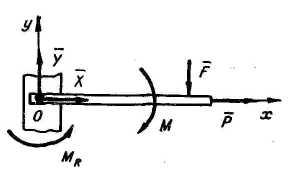
4. Жесткая заделка | |
|
|
Реакция
жесткой заделки состоит из двух
составляющих силы
М (плоская задача). |
|
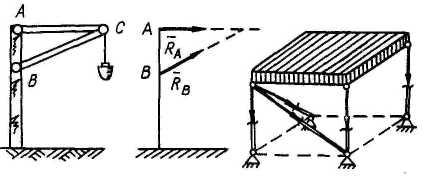
5. Невесомые стержни, закрепленные на концах шарнирами (А, В, С) | |
|
|
Реакции направляются вдоль прямой, соединяющей шарниры. |
|
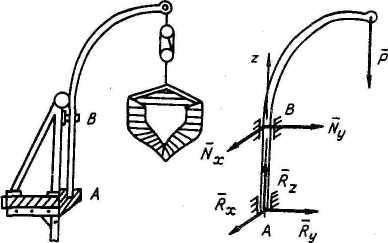
6. Реакция подпятника | |
|
|
В
подпятнике A
возникают три составляющие реакции:
В
подшипнике B
(цилиндрический шарнир) - составляющие
реакции
|
|
7. Сферический шарнир |
|
|
1 - невесомый стержень
2 - сферический шарнир
3 - петля (цилиндрический Шарнир)
|
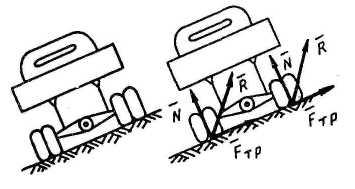
8. Опорная шероховатая поверхность | |
|
|
Реакция
шероховатой поверхности складывается
из двух составляющих: нормальной
|
Реакции при расчленении системы на части
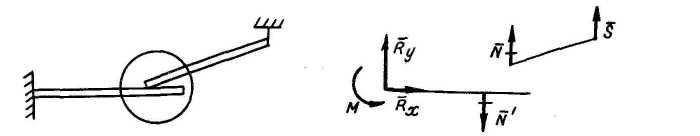
Опора на гладкую поверхность
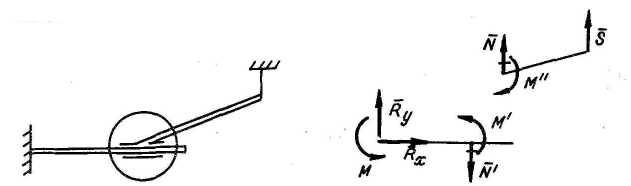
Ползун без шарнира
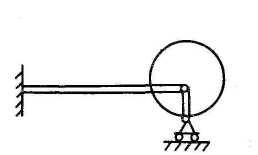
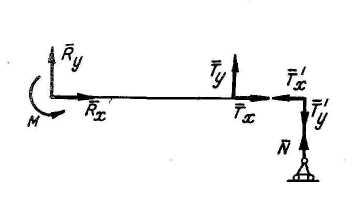
Шарнир
|
Узел мостовой фермы | |
|
|
Расчетная схема |
|
|
|
Вал цилиндрического редуктора и расчетная схема для определения реакций опор (подшипники A и B)
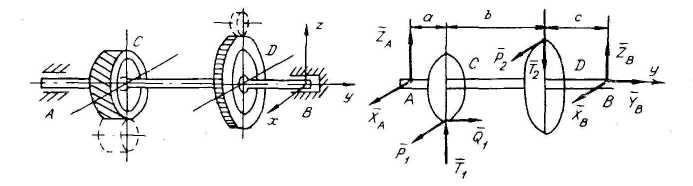
1.8 Система сходящихся сил
Системой сходящихся сил называют систему сил, линии действия которых пересекаются в одной точке:
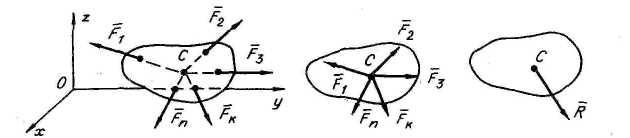
Перенося
силы вдоль их линий действия в точку
пересечения и производя геометрическое
сложение всех векторов сил, можно
получить равнодействующую
![]() данной системы сходящихся сил
данной системы сходящихся сил![]() ;
;![]() .
.
Модуль
равнодействующей равен
![]() ,
где
,
где![]() ,
,
![]() ,
,![]() .При
равновесии
системы сходящихся сил
.При
равновесии
системы сходящихся сил
![]() или в проекциях на оси координат
или в проекциях на оси координат
![]() ;
;![]() ;
;![]() .
.
1. 9 Система пар сил
Если на тело действуют пары сил, произвольно расположенные в пространстве, то такую систему пар можно заменить одной эквивалентной парой сил с моментом, равным геометрической сумме вектор-моментов всех пар сил.
Действительно, учитывая, что вектор-моменты пар сил являются свободными векторами, их можно перенести в произвольную точку и геометрически сложить:
![]() .
.
Модуль
равен
![]() ,
где
,
где![]() ;
;![]() ;
;![]() .
.
При
равновесии
системы пар сил
![]() или в проекции на оси координат:
или в проекции на оси координат:
![]() ;
;![]() ;
;![]() .
.
В
случае, когда система пар сил расположена
в одной плоскости, условием равновесия
является равенство нулю алгебраической
суммы моментов пар сил
![]()
1. 10 Основная теорема статики (метод Пуансо)
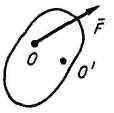
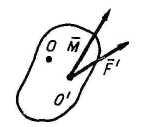
Лемма о параллельном переносе силы: силу можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил, момент которой равен моменту данной силы относительно новой точки приложения:
|
имеем |
добавим |
получим |
|
|
|
|
силы
![]() и
и![]() представляют собой пару сил, момент
которой
представляют собой пару сил, момент
которой![]() .
.
введем
обозначения:
![]() - главный вектор данной системы сил;
- главный вектор данной системы сил;
![]() - главный момент данной системы сил
относительно т. О.
- главный момент данной системы сил
относительно т. О.
Основная теорема статики: произвольную систему сил можно заменить одной силой, приложенной в некоторой точке тела (центре приведения) и равной главному вектору, и одной парой сил с моментом, равным главному моменту системы относительно этой точки:
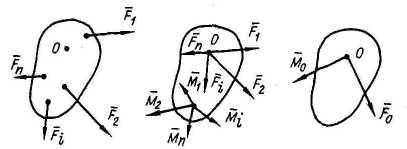
доказательство:
выберем произвольную т. О за центр
приведения заданной системы сил
![]() .
Перенося все силы в т. О согласно лемме
о параллельном переносе силы, получим
систему сходящихся сил и систему пар
сил. Складывая отдельно силы и пары,
находим
.
Перенося все силы в т. О согласно лемме
о параллельном переносе силы, получим
систему сходящихся сил и систему пар
сил. Складывая отдельно силы и пары,
находим![]() и
и![]() .
Таким
образом
.
Таким
образом
![]() .
.