4.4 Критерий устойчивости Найквиста - Михайлова
С помощью критерия устойчивости Найквиста-Михайлова по стационарным свойствам разомкнутой САУ можно судить о нестационарных свойствах замкнутой. Этот критерий был впервые предложен американским ученым Найквистом в 1932г. для анализа устойчивости радиоэлектронных устройств. А.В.Михайлов обобщил его и использовал впервые для анализа устойчивости систем автоматического управления.
Известно, что
характеристическое уравнение замкнутой
САУ, определяющее ее устойчивость,
получается приравниванием нулю
знаменателя передаточной функции
замкнутой системы, т.е.
.
Обозначим
тогда
(4.8)
Если в выражении
(4.8) заменить
на
,
то в числителе получим годограф Михайлова
для замкнутой системы, а в знаменателе
- для разомкнутой. При этом степень
числителя и знаменателя будут одинаковы
и, если замкнутая и разомкнутая системы
устойчивы, то
.
На комплексной
плоскости это обозначает, что вектор
при изменении
от 0 до
не поворачивается вокруг точки
,
или что вектор
не охватывает на комплексной плоскости
точку
при изменении
от 0 до
(рисунок 4.3).
Таким образом, если
разомкнутая САУ устойчива и ее АФХ не
охватывает на комплексной плоскости
точку с координатами
,
то замкнутая САУ будет устойчива.
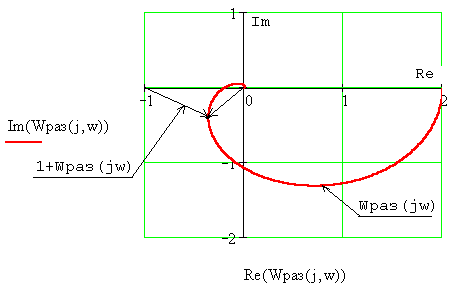
Рисунок 4.3 – Иллюстрация к критерию Найквиста-Михайлова
Если разомкнутая
САУ неустойчива и имеет
неустойчивых корней, а замкнутая САУ
устойчива, то
Таким образом, если
разомкнутая САУ неустойчива и имеет
неустойчивых корней, то для устойчивости
САУ в замкнутом состоянии необходимо,
чтобы АФХ разомкнутой системы охватывала
в положительном направлении точку на
комплексной плоскости с координатами
раз.
Если разомкнутая САУ неустойчива, то число неустойчивых корней можно определить по критерию Михайлова.
В том случае, если разомкнутая САУ находиться на границе устойчивости благодаря наличию нулевых корней, передаточную функцию ее можно записать так:
(4.9)
где
- кратность нулевого корня.
При малых значениях
АФХ нейтральной системы можно представить
так:
|
|
(4.10) |
где
Из выражения (4.10)
следует, что при малых
значение
.
АФХ разомкнутой системы стремиться к
началу координат при увеличении
по одной из осей координат комплексной
плоскости:
при
т.е. АФХ перемещается по отрицательной
мнимой оси;
при
т.е. АФХ перемещается по отрицательной
вещественной оси;
при
т.е. АФХ перемещается по положительной
мнимой оси.
Для анализа устойчивости таких систем справедлив критерий устойчивости Найквиста-Михайлова, если их АФХ дополнить частью окружности бесконечного радиуса, которая начинается на положительной вещественной полуоси, как это показано на рисунке 4.4.
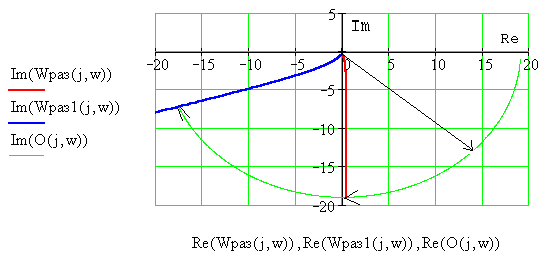
Рисунок 4.4 – Иллюстрация к критерию Найквиста-Михайлова
Из рисунка следует,
что абсолютная устойчивость (устойчивость,
которая не нарушается при уменьшении
коэффициента усиления разомкнутой
системы) может быть получена только при
.
При
может быть получена только условная
устойчивость.