Дворецкий С.И. и др. - Комп. моделир. и оптимизация технологич. процессов и оборуд. [2003]

Перепишем задачу (4.29) – (4.31) в терминах А-задач стохастического программирования: требуется найти m -мерный вектор постоянных величин α* = (α1* , α*2 , ... ,α*m ) , векторы конструктивных dα* и

управляющих zα* переменных такие, что

k =1

терпретированы как вероятности того, что вектор неопределенных параметров θ принимает значения θk , θ = ∫θ P(θ) d , z ) dθ, P(θ) – плотность распределения случайной величины θ .

T

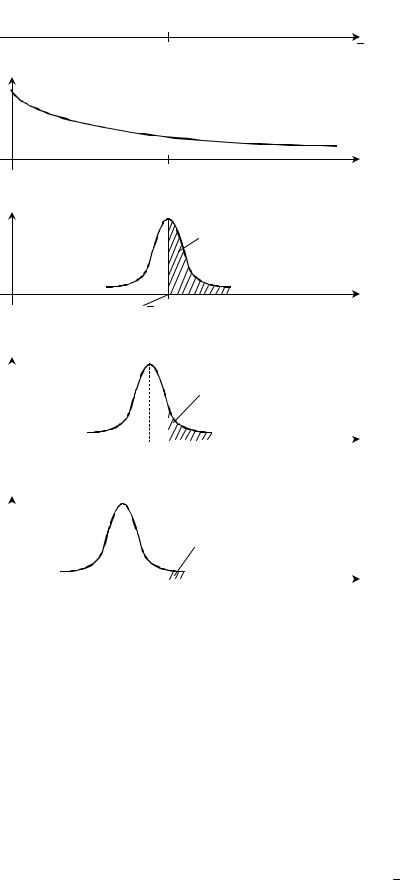
Идея такого подхода, в сущности, очень проста. Поясним ее на примере одномерной задачи стохастического программирования с одним ограничением g(z, θ) ≤ 0 . На рис 4.4, a заштрихована недопусти-

мая область ограничения. Пусть соотношение между целевой функцией M θ{ C(z, θ)} и g(z, θ) такое, как

показано на рис. 4.4, б. Следует заметить, что такое соотношение (кроме, конечно, экзотических случаев) в оптимизационных задачах химической технологии бывает всегда, т.е. наиболее предпочтительные значения целевой функции лежат в недопустимой области (рис. 4.4), поскольку в противном случае ограничение было бы неактивным и его не следовало бы учитывать. В этом случае решение z′ традиционной задачи оптимизации достигается при g(z′, θ) = 0 . Очевидно, при реализации этого решения z′ зна-

чения g(z′, θ) будут иметь случайный разброс вследствие наличия случайной величины θ . На рис 4.4, в показан этот разброс, который может имитироваться на вероятностной модели (z′, θ) .

Взависимости от вхождения случайной величины в функцию g(z′, θ) закон распределения этой функции может изменяться. Следовательно, эта вероятность может быть как меньше, так и больше 0,5. Таким образом, при решении традиционной задачи при θ = θ мы даже не знаем, какова вероятность нарушения технологических ограничений.

Всформулированной выше задаче стохастической оптимизации мы требуем, чтобы эта вероятность была меньше, чем некоторая заданная величина 1−ρзад , где ρзад – заданное значение вероятности выпол-

нения ограничений.

Идея А-задач стохастического программирования заключается в следующем: исходное ограничение задачи заменяется на ограничение вида g(z, α) ≤ α , где α < 0 , т.е. исходное ограничение как бы ужесто-

чается (рис. 4.4, г). После этого решается детерминированная задача оптимизации с новыми ограничениями

min{ C(z, θ) g(z, θ) ≤ α1}.

z

При этом решение задачи z′′ будет соответствовать тому, что технологические ограничения g(z′′, θ) будет равным α1 (рис. 4.4, г). Соответственно, вероятность нарушения ограничения уменьшается по сравнению с ρ1 , т.е. ρ2 < ρ1 , а значение целевой функции возрастает (рис. 4.4, б). Таким образом, мы при-

близились к оптимальному решению задачи, которое изображено на рис. 4.4, д. Отметим, что при выполнении

Рис. 4.4 Геометрическая иллюстрация идеи решения А-задачи стохастической оптимизации

этой процедуры мы не вычисляли вероятность выполнения (нарушения) ограничения на каждом шаге поиска z* . Вычисление Bepθ[ g(z, θ) ≤ 0] производится в оптимальной точке z* для того, чтобы проверить выполнение условия Bepθ[ g(z, θ) ≤ 0] ≥ ρзад . В том случае, если эти условия не выполняются, выбирается

Bepθ[ g(z, θ) ≤ 0] ≥ ρзад или ρ3 ≤1 −ρзад .

Следует заметить, что возможность применения метода А-задач стохастического программирования должна всегда доказываться либо аналитическим доказательством выполнения достаточных условий, либо вычислительным экспериментом, подтверждающим выполнение достаточных условий.

В данном исследовании мы опираемся на результаты наших работ [59, 60], в которых сформулированы достаточные условия, которым должны удовлетворять функции g j (d, z, θ) , Bepθ[ g j (d, z, θ) ≤ 0]

и при выполнении которых решение задачи (4.32), (4.33) – (dα* , zα* , C(dα* , zα* )) – будет являться реше-

нием задачи (4.29) – (4.31).

В соответствии с методом А-задач стохастической оптимизации нами разработан следующий алго-

ритм решения задачи (4.32), (4.33) [59].

Алгоритм 2.

Шаг 1. Задается начальное значение ν = 0 и вектора α(ν) = (α1(ν) , α(2ν) , ... ,α(mν) ) .

Шаг 2. Методом последовательного квадратичного программирования решается задача НЛП

Шаг 3. В точке ( dα(0) , zα(0) ) , которая является решением задачи (4.34) – (4.36), вычисляются вероятности выполнения ограничений с использованием имитационной модели

y= (d, u, θ)

ипроверяется выполнение условий

Bepθ { g j (d, u, y) ≤ 0} ≥ ρ, j J .

Шаг 4. Если вероятностные ограничения не выполняются, т.е. α(ν) Λ , включается алгоритм входа в допустимую область Λ . Простейшим алгоритмом такого типа является уменьшение α(jν) для нару-

шенных ограничений. Далее число ν увеличивается на 1, т.е. ν = ν +1 и следует переход к шагу 2.

Шаг 5. Если вероятностные ограничения выполняются, то вектор α* находим из решения внешней А-задачи оптимизации

В общем случае задача (4.37) может быть решена подходящим методом нелинейного программирования. Однако нами применялись простейший алгоритм коррекции вектора α Λ путем увеличения его компонентов на величину

∆α j = λ(ν) (Bepθ[g j (•) ≤ 0] −ρ),

где λ(ν) – шаг коррекции на ν – ой итерации, подбираемый опытным путем. Поиск α* прекращается, если ∆α j для j становится меньше заранее заданного малого числа ε (точность поиска α* ).

Вычисление вероятностных интегралов производится стандартными методами (Монте-Карло, на аппроксимирующей сетке).

Задача 2. Имеются конструктивные и управляющие переменные. На этапе эксплуатации неопределенные параметры могут быть определены в некоторый момент времени и управляющие переменные могут быть использованы для обеспечения выполнения ограничений.

Для этого случая использовать в качестве критерия выражение Mθ {C* (d, θ) }, где

C* (d, θ) = min C(d, z, θ) g j (d, z, θ) ≤ 0, j J , которое мы применяли для задачи с жесткими ограничениями,

z

нельзя. Это связано с тем, что сам вид этого критерия предполагает выполнение всех ограничений при всех θ из заданной области, т.е. жестким образом. Построим для этого случая критерий оптимизации.

При этом будем использовать следующие обозначения:

пределе при ρзад =1 задача (4.39) – (4.41) переходит в двухэтапную задачу с жесткими ограничениями.

Решение двухэтапной задачи оптимизации (4.39) – (4.41) гораздо сложнее одноэтапной задачи (4.29) – (4.31) и для ее решения также будем использовать метод дискретизации критерия для получения дискретного аналога задачи (4.39) – (4.41). С помощью квадратурной формулы функцию

можно приближенно заменить на функцию

M θ{C* (d, θ)}= ∑γiC* (d, θi ),

Поскольку под знаком суммы задачи оптимизации зависят каждая от своих поисковых переменных, операции суммирования и минимизации можно поменять местами, и задача (4.39)-(4.41) может быть представлена в следующем виде

θ ˆ ≥ ρ .

Bep[ T ] зад

или

при ограничениях

Решение сформулированной задачи возможно с использованием эффективных методов решения задач нелинейного программирования и имитационного моделирования.

Нами разработан алгоритм решения задачи (4.42) – (4.45), базирующийся на методе имитационного моделирования [59].

Задача 3. Имеются конструктивные и управляющие переменные. Вектор неопределенных параметров состоит из двух подвекторов θ1 и θ2 ( θ = (θ1 , θ2 ) ). В подвектор θ1 входят параметры, которые могут быть только определены на стадии эксплуатации процесса, в подвектор θ2 – параметры, имеющие неопределенности на этапе эксплуатации те же, что и на этапе проектирования. Пусть при этом θ1 T 1 и

θ2 T 2 .

Эта задача в большей степени соответствует реальным задачам проектирования, поскольку внешние случайные факторы всегда будут иметь место не только на стадии проектирования, но и на стадии эксплуатации производства. Математическая постановка задачи имеет вид:

где A – штрафной коэффициент; J * – множество индексов ограничений, за нарушение которых берется штраф.

Здесь также отметим, что если существует d D , при котором

При этом сформулированная задача (4.46), (4.47) переходит в двухэтапную задачу с жесткими ограничениями.

Задача 4. Имеются конструктивные и управляющие переменные. На этапе эксплуатации ХТП область неопределенных параметров та же, что и на этапе проектирования. Этот случай соответствует задаче проектирования ХТП, когда на этапе эксплуатации область неопределенных параметров не может быть уточнена.

Эта задача может быть сформулирована (в отличие от задачи 1) следующим образом):

C* = min M θ{C(d, z, θ)},

d , z

при условии

max max g j (d, z, θ) ≤ 0

θ j

или

max g j (d, z, θ) ≤ 0, j J.

θ

Упростим сформулированную задачу. Для этого заменим математическое ожидание с помощью квадратурнойформулы некоторой суммой

M θ {C(d, z, θ)}≈ ∑ νi C(d, z, θ(i) ) ,

l I1

g j (d, z, θ(i) ) ≤ 0, j =1, m; i I2(ν)

и определяем d (ν) , z(ν) . Шаг 3. Решаем m-задач

max gi (d (ν) , z (ν) , θi ), j =1, m

θ T

и определяем m точек θ(i)* , i =1, m . Шаг 4. Образуем множество

R(ν) = {θ(i)* : g j (d (ν) , u (ν) , θ(i)* ) > 0}.

Если это множество пустое, то решение задачи получено. В противном случае перейдем к шагу 5. Шаг 5. Определим

S2 (ν+1) = S2 (ν) R(ν) .

Положим ν = ν +1 и переходим к шагу 2.

Характерной чертой алгоритма 3 является увеличение числа критических точек на каждом шаге, соответственно увеличивается число ограничений. Это является определенным недостатком, поскольку в некоторых случаях при большом числе критических точек число ограничений может стать слишком большим.

Остановимся подробнее на шаге 3. Как правило, характер функций g j неизвестен. В этом случае можно использовать такой подход. Предполагаем на первом этапе, что функции g j выпуклы. В этом случае решение задачи

max gi (d (ν) , z(ν) , θi ), j =1, m .

θ T

находится в одной из вершин параллелепипеда T [42]. В начальное множество критических точек S2(0) включается некоторое количество угловых точек куба T , а на шаге 3 рассчитываются значения функций gi (d (ν) , z(ν) , θi ), j =1, m во всех угловых точках куба T , не принадлежащих множествам S2(ν ) и S1 . Сре-

ди этих точек выбираются m точек, в которых функции gi (d (ν) , z(ν) , θi ), j =1, m принимают наибольшие значения. Далее определим множество критических точек S2(ν+1) = S2(ν) R(ν) и переходим к шагу 2 алго-

ритма 2.

Задача 5. Имеются конструктивные и управляющие переменные. На этапе эксплуатации неопределенные параметры могут быть определены в каждый момент времени. Для обеспечения выполнения ограничений gi (d, z, θ) ≤ 0, j J могут быть использованы конструктивные и управляющие переменные.

Для этого случая условие гибкости (работоспособности) можно записать в виде

θ T z, d j J [g j (d, z, θ) ≤ 0]

или

χ(d) = max min max g j (d, z, θ) ≤ 0.

θ T z, d j J

Изменение конструктивных переменных гибкого аппарата на стадии эксплуатации ХТП возможно за счет его модульно-блочной структуры. Тогда оптимизационная задача в условиях неопределенности на стадии проектирования будет иметь вид

при условии (4.48).

Используя квадратурную формулу, функцию M θ{•} можно приближенно заменить выражением

Mθ{C*(d, z, θ)}≈ ∑νiC*(d, z, θi ),

i I1

где νi – весовые коэффициенты; θi – аппроксимационные точки; I1 – множество индексов аппроксима-

ционных точек.

Операции суммирования и минимизации можно поменять местами и задача может быть представлена в следующем виде

Сформулированная задача также как и задача 4 относится к одноэтапным задачам оптимизации и может быть решена с помощью алгоритма 3.

Задача 6. Формулировка этой задачи та же, что и задачи 2, за исключением того, что условие гибкости (работоспособности) проекта ХТП записывается в логической форме

θ{ z ( j J [g j (d, z, θ) ≤ 0])}

или с учетом эквивалентных соотношений

max g(z) ≤ 0 z g(z) ≤ 0;

z

max g(z) ≤ 0 z g(z) ≤ 0;

z

в виде

В сформулированной задаче существенно различаются роли конструктивных d и технологических переменных z на двух этапах. Переменные d , выбранные на этапе проектирования, естественно, остаются неизменными на всем этапе функционирования процесса. С другой стороны, технологические режимные (управляющие) переменные на этапе функционирования могут настраиваться в зависимости от того, какие значения принимают параметры θ . Фактически в данном случае решается задача выбора

оптимальных коэффициентов запаса для конструктивных переменных, обеспечивающих выполнение технологических ограничений при любых значениях параметров θT . В данном случае также можно считать переменные d и z равноправными и, используя одноэтапную стратегию, решить задачу.

Однако это делать невыгодно, поскольку мы неявно предполагаем, что один раз найденные на этапе проектирования режимные переменные остаются затем неизменными независимо от того, какие фактические значения примут параметры θ . Это может привести в излишне большим коэффициентам запаса. В то же время использование возможности изменять параметры z (с помощью системы управления) на этапе функционирования процесса "облегчает" переменным d удовлетворять ограничениям, что, в свою очередь, позволит уменьшить коэффициенты запаса.

Двухэтапную задачу оптимального проектирования можно записать в виде

при ограничениях (4.48).

Используя прием дискретизации, перепишем последнюю задачу в виде

Решение задачи (4.48) – (4.50) прямыми методами не представляется возможным, поскольку вычисление χ(d) в каждой точке может привести к очень большим объемам вычислений. В связи с этим здесь

будет рекомендована итерационная процедура, основанная на идеях метода "ветвей и границ" [61] и обеспечивающая приближение значений целевой функции (4.49). При этом не требуется непосредственно вычислять величину χ(d) .

В дальнейшем нам потребуются следующие два соотношения:

где x, y – векторы дискретных или непрерывных переменных. Последнее соотношение является оче-

видным.

Введем функцию

ϕ(d, z, θ) = max g j (d, z, θ).

j J

Тогда величина χ(d) имеет вид

χ(d) = max min ϕ(d, z, θ).

Известно, что задача вычисления χU (d) может быть сведена к следующей

χU (d) ≤ 0

является достаточным условием допустимости (работоспособности) проекта, определяемого вектором

Отсюда следует, что если

χL (d) ≥ 0,

то и χ(d) ≥ 0 . Поэтому это условие является достаточным условием недопустимости (неработоспособности) проекта с вектором d . Для определения χ(d ) необходимо решить m задач вида

max min g j (d, z, θ), j 1, m.

θT z Z

Каждая из этих задач эквивалентна следующей

Таким образом, имеем

χL (d) ≤ χ(d) ≤ χU (d) .

(4.55)

Следовательно, вычислив значения χL и χU , получим оценки снизу и сверху величины χ –

критерия гибкости (работоспособности) Гроссмана. Проанализируем физический смысл условия

χU (d) ≤ 0.

Будем искать такой вектор z , который обеспечивает допустимость вектора d при любых θ :

z, θ, j g j (d, z, θ) ≤ 0.

Таким образом, используя этот критерий, мы ищем единственный вектор z , который обеспечивает допустимость вектора d при любых значениях θ . Напомним, что в критерии гибкости Гроссмана

каждому значению θ соответствует свой вектор z , обеспечивающий допустимость вектора d .

Если разность χU −χL мала, то рассмотренный подход дает возможность оценить гибкость ХТП, в

противном случае необходима какая-либо регулярная процедура, позволяющая изменить эту разность. Рассмотрим одну из этих процедур [61, 62]

Разобьем область T на N областей Ti , (i =1, N ). Для каждой области определяем величину

Для этого необходимо решить задачу

χU = max min max max g j (d, z, θ).

i z Z j J θ Ti

Поскольку Ti T , то имеет место неравенство

χUi ≤ χU ,

откуда

χU = max χUi ≤ χU . i

Далее можно показать, что

χ ≤ χU ≤ χU .

Следовательно, получена уточненная верхняя оценка критерия гибкости Гроссмана. Заметим, что чем плотнее покрытие области T , тем ближе будет χU к χ . Однако такой путь может приводить к решению большого числа задач (4.56). В связи с этим рассмотрим другой путь вычисления χ(d ) . Для этого представим критерий χ(d) в виде

χ(d) = max ψ(d, θ),

θ T

где

ψ(d, θ) = min max g j (d, z, θ).

z j

Здесь вычисление χ(d ) сводится к определению точки θ* , в которой функция ψ(d, θ) принимает

максимальное значение.

Для определения этой точки воспользуемся процедурой метода "ветвей и границ" [63]. Цель этой процедуры будет состоять в том, чтобы разбивая область T на все большее число подобластей Ti , по-

В качестве области Tk(νν) берется та из областей Ti(ν) , (i =1, Nν ) , в которой с наибольшей вероятностью на-

ходится оптимальная точка θ* .

Вычислим для каждой области Ti(ν) величину χUi

χUi ≥ max ψ(d, θ) .

θ Ti