Doicu A., Wriedt T., Eremin Y.A. Light scattering by systems of particles (OS 124, Springer, 2006

testing functions are defined and the scalar product of each testing function is formed with both sides of the equation being solved. This results in a system of equations which is referred to as the element matrix equations. The element matrices are assembled into the global matrix of the entire “structure” and the resulting system of equations is solved for the unknown expansion coe cients.

2.1.6 Spherical Particles

An interesting feature of the null-field method is that all matrix equations become considerably simpler and reduce to the corresponding equations of the Lorenz–Mie theory when the particle is spherically. For a spherical particle of radius R, the orthogonality relations of the vector spherical harmonics show that the Qpq matrices are diagonal

is the relative refractive index of the particle with respect to the ambient medium. The above relations are not suitable for computing the Qpq matrices. Denoting by An and Bn the logarithmic derivatives [2, 17]

and using the recurrence relation (cf. (A.8))

[xzn (x)] = xzn−1(x) − nzn(x) ,

where Ψn stands for An and Bn, and a stable scheme for computing Ψn relies on a downward recursion. Beginning with an estimate for Ψn, where n is larger that the number of terms required for convergence, successively lower-order logarithmic derivatives can be generated by downward recursion. It should be noted that the downward stability of Ψn is a consequence of the downward stability of the spherical Bessel functions jn (see Appendix A).

The transition matrix of a spherical particle is diagonal with entries

Tmn,m11 1n1 = Tn1δmm1 δnn1 ,

Tmn,m22 1n1 = Tn2δmm1 δnn1 ,

where Lµ and Rµ are given by (1.58) and (1.59), respectively, and

are the wave numbers of the leftand right-handed type waves. The transition matrix of a homogeneous, chiral particle then becomes

The expressions of the elements of the Q11chiral matrix are similar but with M 1ν and N 1ν in place of M 3ν and N 3ν , respectively. It must be noted that in case the

established in Sect. 1.3 regarding the series representations of the electromagnetic fields propagating in anisotropic media, we see that the scattering problem can be solved if we approximate the surface fields by finite expansions of vector quasi-spherical wave functions X and Y (cf. (1.48)–(1.53)),

The transition matrix of an uniaxial anisotropic particle then becomes

T = −Q11anis (ks, ki, mrz ) Q31anis (ks, ki, mrz ) −1 ,

where mrz = εiz /εs, and for µi = µs, the elements of the Q31anis matrix are given by

The expressions of the elements of the Q11anis matrix are similar but with M 1ν and N 1ν in place of M 3ν and N 3ν , respectively. Using the properties of the

vector quasi-spherical wave functions (cf. (1.47)) it is simple to show that for εiz = εi, the present approach leads to the T -matrix solution of an isotropic particle.

2.4 Inhomogeneous Particles

In this section, we consider electromagnetic scattering by an arbitrarily shaped, inhomogeneous particle with an irregular inclusion. Our treatment follows the analysis of Peterson and Str¨om [189] for multilayered particles and is similar to the approach used by Videen et al. [243] for a sphere with an irregular inclusion. Note that an alternative derivation using the Schelkuno ’s equivalence principle has been given by Wang and Barber [248].

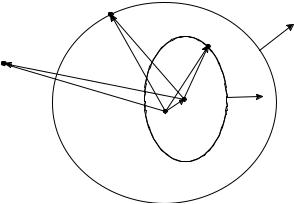
106 2 Null-Field Method

2.4.1 Formulation with Addition Theorem

In the present analysis we will derive the expression of the transition matrix by using the translation properties of the vector spherical wave functions. The completeness property of the vector spherical wave functions on two enclosing surfaces, which is essential in our analysis, is established in Appendix D.

The scattering problem is depicted in Fig. 2.2. The surface S1 is defined with respect to a Cartesian coordinate system O1x1y1z1, while the surface S2 is defined with respect to a Cartesian coordinate system O2x2y2z2. By assumption, the coordinate system O2x2y2z2 is obtained by translating the coordinate system O1x1y1z1 through r12 and by rotating the translated coordinate system through the Euler angles α, β and γ. The boundary-value problem for the inhomogeneous particle depicted in Fig. 2.2 has the following formulation.

Given the external excitation Ee, He as an entire solution to the Maxwell equations, find the scattered field Es, Hs and the internal fields Ei,1, Hi,1and Ei,2, Hi,2 satisfying the Maxwell equations

Ds

Fig. 2.2. Geometry of an inhomogeneous particle

108 2 Null-Field Method

For the general null-field equation (2.69) in Ds, we proceed analogously but restrict r1 to lie on a sphere enclosing Di. We then have