Rauk Orbital Interaction Theory of Organic Chemistry

EXERCISES 249

What is the relationship between:

(viii)H2 and H7?

(ix)H3 and H8?

(x)H5 and H9?

(xi)F2 and F3?

(c)How many separate 13C NMR chemical shifts should one observe

(i)Under achiral conditions?

(ii)Under chiral conditions?

(d)Replace two H atoms by D in such a way that:

(i)The only symmetry element is a mirror plane s.

(ii)The only symmetry element is a C2 axis.

(iii)The only symmetry element is a center of inversion i.

(iv)The molecule is asymmetric.

Answers. (a) C2h; (b) (i) H1, H2, (ii) H3, H4, (iii) H6, H9, (iv) H1, H8, (v) F1, F3, (vi) F1, F2, (vii) none, (viii) enantiotopic, (ix) diastereotopic, (x) homotopic, (xi) diastereotopic; (c) (i) four (uncoupled), (ii) six (uncoupled); (d) (i) H5, H6, (ii) H5, H9,

(iii) H6, H9, (iv) H1, H9.

6.Analyze the stereochemical relationships between the groups of cis-2,5,dimethyl- cyclopentanone 5. Speci®cally, Identify at least one pair of groups for each of the following relationships: homotopic, enantiotopic, diastereotopic, or constitutionally heterotopic. Note: if there are no pairs of a given kind, say so.

Chapter 2 and Appendix A

1.Choose a small molecule and carry out a HF/STO-3G calculation, including a geometry optimization. Repeat, using the B3LYP/6-31G* level of theory.

(a)State the name of the compound and draw a clear representation of its structure, correctly oriented in the coordinate system (standard orientation). What is its molecular point group?

(b)Plot the valence MO energy levels, including a few of the unoccupied MOs. Identify the HOMO and LUMO. Make note of the position of the core levels.

(c)Sketch the two highest occupied and two lowest unoccupied molecular orbitals on the basis of the STO-3G MO coe½cients. Note which atoms have the largest coe½cients in each MO. Is there any signi®cance to this? Do the MOs transform according to the irreducible representations of the molecular point group?

(d)Comment on the population analysis. Is it reasonable in view of the elemental composition, concepts of electronegativity and resonance, and the molecular symmetry? Compare population analyses for the two levels of theory.

250EXERCISES

(e)Find literature references to previous experimental and theoretical work on the compound you chose. Compare the computed properties (geometry, IP, dipole moment, total energy) with experimental and/or other theoretical studies.

(f ) Prepare a 10-min discourse based on the points of the above questions (with a brief introduction) for presentation before the class. Include discussion of the technical aspects of the calculation.

2.Write a one-page essay on the properties and use of orbitals in the description of many-electron systems. Your answer should include at least ten distinct points. Use of equations is encouraged, but the equations should be verbally interpreted.

Answer. Orbitals are one-electron wave functions, f(1). The fact that electrons are fermions requires that each electron be described by a di¨erent orbital. The simplest

form of a many-electron wave function, C…1; 2; . . . ; Ne†, is a simple product of orbi-

tals (a Hartree product), f1…1†f2…2†f3…3† fNe …Ne†. However, the fact that electrons are fermions also imposes the requirement that the many-electron wave function be antisymmetric toward the exchange of any two electrons. All of the physical requirements, including the indistinguishability of electrons, are met by a determinantal wave function, that is, an antisymmetrized sum of Hartree products, F…1; 2; 3; . . . ; Ne† ˆ

jf1…1†f2…2†f3…3† fNe …Ne†j. If F…1; 2; 3; . . . ; Ne† is taken as an approximation of C…1; 2; . . . ; Ne†, i.e., the Hartree±Fock approximation, and the orbitals varied so as

to minimize the energy expectation value,

…

FHF dt

E ˆ …

F F dt

where H is the correct electronic Hamiltonian, one ®nds that the orbitals must be eigenfunctions of a one-electron operator, the Fock operator F…1†:

In the Fock operator, the ``core'' Hamiltonian h…1† does not depend on the orbitals, but the Coulomb and exchange operators Jb…1† and Kb…1† depend on fb…1†. If F…1; 2; 3; . . . ; Ne† is constructed from the lowest energy Ne orbitals, one has the lowest possible total electronic energy. By Koopmans' theorem, the negative of the orbital energy is equal to one of the ionization potentials of the molecule or atom.

If one is dealing with a molecule, the orbital is called a molecular orbital (MO) and is constructed as a linear combination of atom-centerd basis functions, the coe½cients (weights) of which are also determined by application of the variational method to minimize the MO energies.

3.Write one paragraph on the application of the variational principle using each of the following words or phrases in the correct context (not necessarily in the order given; underline each occurrence):

EXERCISES 251

(a)SchroÈdinger equation

(b)Expectation value

(c)CI wave function

(d)Single determinantal wave function

(e)Hamiltonian matrix

4.Write one paragraph on any aspect of Hartree±Fock theory but incorporate each of the following words or phrases in the correct context (not necessarily in the order given; underline each occurrence):

(a)Single determinantal wave function

(b)Fock operator

(c)Molecular orbital energy

(d)Exchange integrals

(e)Basis set

5.The following questions deal with a speci®c application of ab initio RHF theory to ethylene (C2H4).

(a)Using summation notation, write the electronic nonrelativistic Hamiltonian operator for ethylene.

(b)Using any notation which makes it clear, show a single determinantal RHF wave function for ethylene.

(c)Assuming that the spatial MOs of part (b) are expanded in a STO-3G basis set:

(i)What is the size of the basis set?

(ii)Which basis functions are likely to have the largest coe½cients in the lowest occupied MO? in the highest occupied MO? Explain brie¯y.

6.In Hartree±Fock theory, the many-electron wave function is expressed as a single Slater determinant, conveniently abbreviated as

The molecular orbitals fi are, by convention, listed in order of increasing energy.

(a)Why is (1) a satisfactory representation of a many-electron wave function?

(b)What conditions must be satis®ed by the MOs in order that (1) represents the single determinantal wave function of lowest possible energy?

(c)State some mathematical properties of the MOs (involving integration).

(d)State some relationships involving the MOs of (1) if (1) were a restricted Hartree±Fock wave function.

(e)The set of MOs are usually expressed as a coe½cient matrix. Why?

(f ) Explain the relationship between MO energy, total electronic energy, and total molecular energy (which de®nes the Born±Oppenheimer potential energy hypersurface).

(g)Write a single determinantal wave function for the molecular ion, M‡, in its ground state. What is its energy relative to the energy of (1).

(h)What are virtual or unoccupied MOs?

252EXERCISES

(i)Write a single determinantal wave function for the molecule in its lowest excited state. What is its energy relative to the energy of (1).

(j)Express the permanent dipole moment of a molecule in terms of MOs.

Chapter 3

1.Draw a general two-orbital interaction diagram in which the two unperturbed orbitals are of di¨erent energy. Label the diagram and indicate relationships which exist between the labeled components.

2.Use a two-orbital interaction diagram to explain or predict some feature of each of the following molecules:

Answer to 2(ii). We note that the structure as drawn has one side which is a carbocation and the other an amine. We should immediately ask whether the presence of the amino group modi®es the Lewis acidity of the cationic center using methyl carbocation as a reference and whether the properties of the amine, compared to, for example, ammonia, might be a¨ected by the presence of the cationic site. Amines, like ammonia, have a pyramidal (nonplanar) geometry and are moderately basic. How do the properties of this species compare to these properties which are characteristic of amines? The two ends are connected by a single bond. Single bonds exhibit relatively unhindered rotation and have characteristic lengths and stretching vibrational frequencies. Do these properties compare with those of methylamine, or are they signi®cantly di¨erent? Is the CÐN bond longer or shorter? Is rotation more or less hindered? Is the CÐN stretching frequency higher or lower? All of these questions may be answered using the simple interaction diagram in Figure B3.1, constructed from frontier orbitals of the two interacting fragments, both of which are tricoordinated centers and therefore have only one valence orbital each. On the left-hand side is the empty 2p orbital of the cationic center, and on the right is the nonbonded orbital of the amine, which may also be a 2p orbital if the amine is planar or it may be the spn hybrid orbital of a nonplanar tricoordinated center. What does the diagram tell us? We note immediately that there are two electrons and so the interaction is favorable. The geometry will change in such a way as to maximize the interaction. In other words, the N atom will become planar and one end of the CÐN bond will rotate relative to the other to maximize the interaction, bringing both ends into coplanarity. There is appreciable p bond character between the C and the N. Thus the bond will be shorter than a typical CÐN single bond, as in methylamine, The barrier to torsion about the bond will be substantially higher, and the stretching frequency will also be higher. In terms of basicity, since the nitrogen lone pair has decreased in energy and the coe½cient at N is smaller (it would have been 1 before the interaction), the basicity is less than that of a typical amine. In terms of Lewis acidity, the LUMO is higher in energy than in our reference methyl cation, the coe½cient at C is smaller (it also would have been 1 before

EXERCISES 253

Figure B3.1. Interaction diagram for [H2CÐNH2]‡.

the interaction), and the Lewis acidity and electrophilicity will have decreased. By the same token, it is more di½cult to reduce (add a electron) than a methyl cation.

3.Use simple orbital interaction diagrams to explain each of the following:

(a)The bonding in

(b)Bonazzola and co-workers (Bonazzola, L.; Michaut, J. P.; Roncin, J., Can. J. Chem., 1988, 66, 3050) have shown by ESR spectroscopy that the singly ionized thiirane cation radical, [thiirane]‡:, forms a 1 : 1 complex with thiirane itself. Suggest a structure for the complex. Note: Thiirane is thiacyclopropane

sion of the structures of hydrazines and their ionization potentials, see Klessinger, M.; Rademacher, P., Angew. Chem. Int. Ed. Engl., 1979, 18, 826.

Answer to 3(a). We are asked here to provide an interaction diagram which will illustrate the nature of the molecular orbitals which contain the three electrons which are involved in binding together the two sulfur atoms. We note that in the absence of an interaction between them, each sulfur atom is a bent dicoordinated atom and as such has two frontier orbitals, a pure p orbital perpendicular to the plane of the s bonds to S and an spn hybrid orbital of lower energy directed along the line bisecting the angle made by the s bonds and in the same plane. In the case of sulfur the p orbital is 3p, and the spn hybrid has rather little ``p'' character …n < 1†. To set up the interaction diagram, one must have an appreciation of the limitations imposed by the s framework, which form an 8-membered ring. Inspection

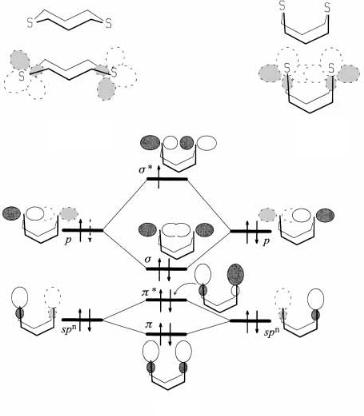
254 EXERCISES

…c†

Figure B3.2. 1,5-Dithiacyclooctane: (a) staggered conformation; (b) folded conformation. (c) Interaction diagram in answer to question 3(a) for the bonding in the radical cation.

of molecular models quickly reveals that among the possible conformations of the 8-membered ring are two, as shown in Figures B3.2a and B3.2b, with the valence orbitals superimposed on the molecular skeleton. In the staggered conformation, the sulfur atoms are too far apart to interact. This is the desirable situation in the neutral molecule since all of the nonbonding orbitals are ®lled and any interaction would be of the four-electron, two-orbital type, which is repulsive. Maximum interaction occurs in the folded conformation (Figure B3.2b). The interaction diagram is shown in Figure B3.2c. The spn orbitals su¨er a weak p-type interaction while the p orbitals interact more strongly in a s fashion. If one, as in this case, or two electrons [see question 4(b)] are missing, then the interaction is favorable and the cation (or dication) will adopt the folded geometry. The three-electron ``bond'' has two electrons in the s orbital and one in the s orbital, for a net attraction. The strength of the three-electron ``SÐS bond'' is approximately 115 kJ/mol (James, M. A.; Illies, A. J., J. Phys. Chem., 1996, 100, 15794±15799). A suitable answer to this question could have ignored the weaker interactions of the spn orbitals. Note that diseleno

EXERCISES 255

Figure B3.3. Interaction diagrams for (a) staggered and (b) perpendicular conformations of hydrazine.

radical cations undergo similar bonding (Cordova-Reyes, I.; Hu, H.; Gu, J.-H.; VandenHoven, E.; Mohammed, A.; Holdcroft, S.; Pinto, B. M., Can. J. Chem., 1996, 74, 533±543).

Answer to 3(c). Each nitrogen atom of hydrazine is tricoordinated and pyramidal. The frontier valence orbital at each site is an spn hybrid directed along the axis of the trigonal pyramid. Both are doubly occupied, and the two spn orbitals su¨er a repulsive four-electron, two-orbital interaction, as shown in Figure B3.3. If the lonepair orbitals are aligned as shown in Figure B3.3a, the intrinsic interaction is larger because the overlap is larger than in the case depicted in Figure B3.3b, where the two hybrid orbitals are almost perpendicular to each other and therefore overlap less. Larger overlap is accompanied by a larger di¨erence between DeU and DeL, that is, a larger repulsion. Therefore, hydrazine adopts the apparently more crowded perpendicular conformation to minimize the repulsive interaction.

4.Use two-orbital interaction diagrams to explain the observed features of the following systems. Note: A clear orbital interaction diagram includes pictures of the orbitals before and after the interaction and shows the disposition of the electrons. A brief verbal explanation of the diagram is also desirable. If more than two orbitals seem to be involved, use your judgment to choose the two most important orbitals.

256EXERCISES

(a)Hydrogen disul®de, S2H2, has a dihedral angle close to 90 :

(b)The two sulfur atoms in 1,5-dithiacyclooctyl dication are su½ciently close to say

that a bond exists between them [see answer to 3(a)]:

(c)Ammonia is more basic than phosphine. (Hint: Use a proton as the Lewis acid for your answer.)

(d)The NH2 group of formamide, NH2CHO, is ¯at, whereas the nitrogen atom of most amines is pyramidal.

(e)Nucleophilic attack on the carbonyl group of ketones, R2CÐO, is catalyzed by Lewis acids.

Answer to 4(c). The two-orbital interaction diagrams for NH3 ‡ H‡ and PH3 ‡ H‡ must be compared (see Figure B3.4). These should be drawn on the same energy scale. Thus the energy of the 1s orbital of H is at the same level in both diagrams, the nonbonded orbital nN of ammonia is lower in energy, and nP, the nonbonded orbital of PH3, is in between. Because P is a third-row element, the intrinsic interaction matrix element hPH will be substantially less than hNH, and both DeL and DeU will depend on it rather than on the energy di¨erence (see the discussion of the halogens in Chapter 4). Two consequences ensue from the small DeL. The PÐH bond is intrinsically weaker toward both homolytic and heterolytic dissociation. The

Figure B3.4. Two-electron, two-orbital interaction diagrams for (a) NH3 ‡ H‡ and (b) PH3 ‡ H‡.

EXERCISES 257

antibonding orbital sPH is lower in energy and more polarized than sNH, as a consequence of which phosphonium (PH‡4 ) is more acidic than ammonium (NH‡4 ). Both results are consistent with higher basicity for ammonia than phosphine.

Answer to 4(d). This question asks us to explain a structural change, pyramidal to planar, that distinguishes the tricoordinated nitrogen atom of amides from amines in general. Stuctural changes may ensue from a minimization of repulsive interactions (four-electron, two-orbital) and/or maximization of attractive interactions (twoelectron, two-orbital). The latter is almost always the case, although question 3(c) dealt with an exception. We therefore adopt a two-electron, two-orbital interaction diagram where the ``interacting'' fragment orbitals are the LUMO of the carbonyl group and the occupied valence orbital of a neighboring tricoordinated nitrogen. Since one of the interacting orbitals (the carbonyl group orbital) is a complex orbital, the interaction will be treated as coming entirely from the orbitals of the two atoms closest to each other, the N and the C. According to general principles, the LUMO of the CÐO group is the pCO, which is polarized toward C (the less electronegative end), and so should interact strongly with the single orbital of N. This is p if the nitrogen is planar and spn if it is pyramidal. The two situations are depicted in Figures B3.5a and B3.5b. The interaction is more favorable if the overlap is maximized. The p-type overlap is maximized if the two orbitals are both p orbitals with their axes parallel (Figure B3.5b). As a consequence, the nitrogen becomes planar and the plane of the NH2 group coincides with the plane of the carbonyl group. The preceding discussion is su½cient to answer the question of nitrogen planarity. Many other properties of the amide group can be explained on the basis of the same diagram. The amide group is discussed in greater detail in Chapter 8 and a more general interaction diagram is provided there (Figure 8.6a).

Figure B3.5. Two-electron, two-orbital interaction diagrams for (a) pyramidal N and (b) planar N.

258 EXERCISES

5.Rohl®ng and Hay recently determined the geometry of FOOF, the ¯uoro analog of hydrogen peroxide (Rohl®ng, C. M.; Hay, P. J., J. Chem. Phys., 1987, 86, 4518±

4522). The geometry is unusual in three respects: (a) the OÐF bonds are unusually

usually short (1.217 A compared to 1.42 A in HOOH), and (c) the FOOF torsion angle is almost 90 …87:5 †. Explain all three features.

Answer. This question asks us to explain structural features in FOOF which are unusual compared to HOOH (or alkyl peroxides for that matter). The underlying reason is the maximization of an attractive two-orbital, two-electron interaction between a nonbonded p orbital of one oxygen and a low-lying sOF orbital of the adjacent OÐF bond. This interaction is analogous to that exhibited in the anomeric e¨ect in sugars. The interaction is mirrored for the other OÐOF pair. The orbital interaction diagram is shown in Figure B3.6. The characteristics of the s OÐF bond may be deduced from the orbital interaction diagram shown in Figure B3.6a. The LUMO is low lying and polarized toward the less electronegative O atom. Since neither O nor F undergoes signi®cant hybridization, the orbitals involved in this bond are essentially 2p orbitals. The dicoordinated oxygen has two valence orbitals, a higher occupied 2p orbital (which is elevated somewhat by being involved in a four-electron, two-orbital interaction with the F atom) and a lower occupied orbital which is formally an spn hybrid, but which in fact is essentially the unhybridized 2s orbital of oxygen. The primary interaction, shown in Figure B3.6b, is between the 2p valence orbitals of oxygen atom …nO† and the adjacent sOF unoccupied orbital. This

Figure B3.6. (a) Two electron, two-orbital interaction diagrams for an OÐF bond; (b) twoelectron, two-orbital interaction diagram for the donor±acceptor interaction in FOOF.