2 Верификация программ

Вспомним, что четвертая фаза процедуры решения задачи, согласно схеме, предложенной математиком Полиа (см. раздел 4.3), заключается в оценке точности работы программы или верификации (verification) и определении его потенциала как инструмента для решения других задач. Важность первой части этой фазы мы проиллюстрируем следующим примером.

Путешественник, у которого есть золотая цепочка из семи звеньев, должен остановиться в уединенном отеле на семь ночей. Плата за каждую проведенную в отеле ночь составляет одно звено его цепочки. Какое наименьшее число звеньев необходимо разрезать, чтобы путешественник мог платить владельцу отеля одно звено каждое утро, не внося плату заранее?

Первым делом уясним себе, что нет необходимости разрезать все звенья. Если мы разрежем только второе звено, то и первое, и второе будут отделены от остальных пяти звеньев. Следуя этому, можно прийти к решению разрезать только второе, четвертое и шестое звенья цепочки. В результате все звенья окажутся свободными, причем только три из них будут разрезанными (рис. 4). Более того, любое меньшее число разрезов оставит два звена соединенными, поэтому мы заключаем, что правильный ответ для этой задачи — три звена.

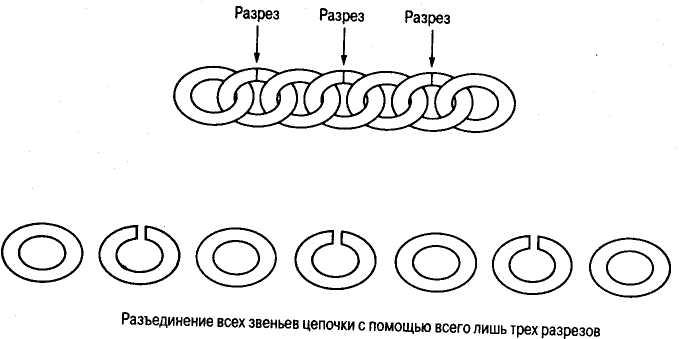
Рисунок 4 - Разделение всех звеньев цепочки с помощью лишь трех разрезов

Однако, рассмотрев задачу более внимательно, можно заметить, что если разрезать только третье звено, то получится три фрагмента цепочки, состоящие из одного, двух и четырех звеньев (рис. 5). С этими фрагментами мы можем поступить следующим образом.

Первое утро. Отдать владельцу отеля одно звено. Второе утро. Забрать у владельца отеля одно звено и отдать ему фрагмент цепочки из двух звеньев. Третье утро. Отдать владельцу отеля одно звено. Четвертое утро. Забрать у владельца отеля три отданные ему ранее звена и отдать ему фрагмент цепочки из четырех звеньев. Пятое утро. Отдать владельцу отеля одно звено. Шестое утро. Забрать у владельца отеля одно звено и отдать ему фрагмент цепочки из двух звеньев. Седьмое утро. Отдать владельцу отеля одно звено.

Рисунок 5 - Решение задачи с помощью лишь одного разреза

Следовательно, тот ответ, который мы считали правильным, на самом деле неверен. Как же убедиться, что новое решение действительно правильно? В качестве доказательства можно привести следующее рассуждение. Поскольку в первое утро необходимо отдать владельцу отеля одно звено, придется разрезать, по крайней мере, одно звено цепочки. Но так как в новом варианте решения требуется разрезать только одно звено, то это решение должно быть оптимальным.

Применительно к программированию этот пример демонстрирует различия между программой, которая выглядит правильной, и программой, которая действительно является правильной. Это не всегда одно и то же. Специалистам в области обработки данных известно множество ужасных историй о том, как программное обеспечение, которое считалось безусловно правильным, все же отказывало в критический момент, поскольку возникшая ситуация оказывалась для него совершенно непредвиденной. Следовательно, верификация программного обеспечения — это важное и необходимое дело, а поиск эффективных методов верификации является активным направлением исследований в области компьютерных наук.

Одно из самых современных направлений в этой области заключается в использовании методов формальной логики для доказательства корректности программ. Это означает, что Цель лекции проводимых исследований состоит в применении формальной логики для доказательства того факта, что реализованный данной программой алгоритм делает именно то, для чего он предназначен. Основополагающий тезис заключается в том, что при сведении процесса верификации к формальной процедуре мы застрахованы от некорректных умозаключений, вытекающих из интуитивной аргументации, как это было в случае с задачей о золотой цепочке. Давайте рассмотрим данный подход к верификации программ более подробно.

Подобно тому, как формальное математическое доказательство основывается на аксиомах (геометрические доказательства часто базируются на аксиомах Евклидовой геометрии, тогда как доказательства других утверждений — на аксиомах теории множеств), формальное доказательство правильности программы основывается на спецификациях, в соответствии с которыми эта программа разрабатывалась. Чтобы доказать, что программа правильно сортирует списки имен, мы можем начать с предположения о том, что на вход программы подается список имен. Если программа создана для вычисления среднего значения одного или более положительных чисел, мы можем предположить, что исходными данными для программы является одно или несколько положительных чисел. Короче говоря, доказательство корректности начинается с предположения о том, что в начале работы программы удовлетворены некоторые условия, называемые предварительными условиями (precondition), или предусловиями.

Следующий этап доказательства корректности заключается в рассмотрении того, как следствия из этих предусловий распространяются по программе. С этой Цель лекциию исследователи изучили различные программные структуры, пытаясь установить, как выполнение данной структуры влияет на утверждение, о котором до выполнения этой структуры было известно, что оно истинно. Например, пусть определенное утверждение о значении переменной Y перед выполнением приведенной ниже инструкции было истинно:

X ← Y

После выполнения этой инструкции то же утверждение можно сделать о значении переменной X. Например, если перед выполнением инструкции значение переменной Y отличалось от 0, то можно сделать заключение, что после выполнения этой инструкции значение переменной X также будет отличаться от 0.

Несколько более сложным случаем является выполнение оператора if-then-else, например, следующего вида:

if (условие) then {инструкция 1} else {инструкция 2}.

Если в этом примере известно, что некоторое утверждение было истинно перед выполнением данной структуры, то непосредственно перед выполнением инструкции 1 мы знаем, что истинны как это утверждение, так и проверяемое условие. В то же время, если должна выполняться инструкция 2, мы знаем, что должны быть истинны исходное утверждение и отрицание проверяемого условия.

Обсуждаемые в тексте проблемы верификации касаются не только программного обеспечения. Столь же важно получить гарантии, что выполняющая программу аппаратура также не содержит ошибок. Это подразумевает верификацию, как разрабатываемых схем, так и конструкции всей машины. И в этом случае полученные результаты в значительной степени зависят от тестирования, задача которого, как и в случае с программным обеспечением, — выявить скрытые ошибки. Показателен пример машины Mark 1, созданной в Гарвардском университете в 1940 году, монтажные ошибки в которой оставались необнаруженными в течение многих лет. Более "свежий" пример — ошибки в блоке выполнения операций с плавающей точкой, имевшие место в первых микропроцессорах типа Pentium. В обоих случаях существующие ошибки были выявлены до каких-либо серьезных последствий.

Если следовать правилам, приведенным выше, доказательство корректности программы осуществляется путем определения положений, называемых утверждениями, которые устанавливаются в различных точках программы. В результате получается набор утверждений, каждое из которых является следствием предусловий программы и последовательности инструкций, приводящей к той точке программы, где установлено данное утверждение. Если утверждение, установленное подобным образом в конце программы, соответствует спецификациям того, что требуется получить на ее выходе, то можно сделать заключение о правильности программы.

В качестве примера рассмотрим типичную циклическую структуру while-do, представленную на рис. 6. Предположим, как следствие предусловий, заданных в точке А, мы можем установить, что определенное утверждение истинно при каждой проверке условия окончания цикла (точка В) на протяжении всего процесса повторения. Такое утверждение внутри цикла называется инвариантом цикла (loop invariant). Как только повторение завершается, выполнение переходит к точке С, где мы можем заключить, что истинны как инвариант цикла, так и условие его окончания. (Инвариант цикла остается истинным, поскольку проверка условия окончания не изменяет никаких величин в программе, а условие окончания истинно, поскольку в противном случае цикл бы просто не завершился.) Если комбинация этих положений означает то, что мы хотим видеть на выходе, наше доказательство корректности можно завершить, просто показав, что компоненты инициализации и модификации цикла в конечном счете приводят к условию окончания.

Рисунок 6 - Использование формального утверждения для проверки правильности оператора цикла while-do

Этот метод анализа можно применить к приведенному выше алгоритму сортировки методом вставки (см. рис. 1). Внешний цикл в этой программе основан на следующем инварианте цикла:

Каждый раз при выполнении проверки условия окончания цикла имена, предшествующие N-му элементу, образуют отсортированный список.

Условие окончания этого цикла формулируется следующим образом:

Значение N больше, чем длина списка.

Таким образом, как только цикл завершится, мы будем знать, что оба условия должны быть выполнены, а это означает, что весь список будет отсортирован.

К сожалению, методы формальной верификации программ не настолько хорошо разработаны, чтобы их можно было использовать в приложениях общего типа. Сегодня в большинстве случаев "верификация" программного обеспечения производится посредством его тестирования при различных исходных условиях, что весьма ненадежно. Верификация с помощью тестирования не доказывает ничего иного, кроме того, что программа правильно работает в тех условиях, в которых ее проверяли. Любые дополнительные заключения — это всего лишь предположения. Ошибки, содержащиеся в программе, чаще всего являются следствием оплошности и недосмотра, что может произойти и при тестировании. В результате ошибки в программе, такие как в задаче с золотой цепочкой, могут остаться и часто остаются незамеченными, хотя были потрачены значительные усилия, чтобы этого избежать. Драматический случай произошел в компании AT&T. Ошибка в программном обеспечении, управляющем 114 телефонными станциями, оставалась незамеченной с момента его установки в декабре 1989 года и вплоть до 15 января 1990 года, когда исключительное стечение обстоятельств привело к тому, что за девять часов было беспричинно заблокировано примерно 5 миллионов телефонных звонков.