2 Ошибки передачи данных

Когда информация передается между различными частями компьютера, или с Земли на Луну и обратно, или просто оставляется на запоминающем устройстве, существует вероятность того, что полученный двоичный код не тождественней исходному коду. Частицы пыли или жира на магнитном носителе или сбой схемы могут привести к неправильной записи или к неправильному чтению данных. Кроме того, фоновое излучение некоторых устройств может привести к изменению кода, хранящегося в оперативной памяти машины.

Для решения таких проблем было разработано большое количество методов кодирования, позволяющих обнаружить и даже исправить ошибки. Сегодня эти методы включены во внутренние составляющие вычислительных машин и не видны пользователю. Тем не менее их наличие является важным и составляет значительную часть научных исследований. Поэтому мы рассмотрим некоторые из этих методов, обеспечивающих надежность современного компьютерного оборудования.

Контрольный разряд четности. Простой метод обнаружения ошибок основывается на том принципе, что если известно, что обрабатываемый двоичный код должен содержать нечетное число единиц, а полученный код содержит четное число единиц, то произошла ошибка. Для того чтобы использовать этот принцип, нам нужна система, в которой каждый код содержит нечетное число единиц. Этого легко достичь, добавив дополнительный разряд, контрольный разряд соответствия (parity bit), на место старшего разряда. (Следовательно, каждый 8-битовый код ASCII станет 9-битовым, а 16-битовой дополнительный код станет 17-битовым.) В каждом случае мы присваиваем этому разряду значение 1 или 0, так чтобы весь код содержал нечетное число единиц. Например, ASCII-код буквы А становится 101000001 (контрольный разряд четности 1), а код буквы F становится 001000110 (контрольный разряд четности 0) (рис. 1.28). Хотя 8-битовый код А содержит четное число единиц, а 8-битовый код F — нечетное, 9-битовый код этих символов содержит нечетное количество единиц. Теперь, когда мы модифицировав нашу систему кодирования, код с четным числом единиц будет означать, что произошла ошибка и что обрабатываемый двоичный код — неправильный.

Рисунок 1 - ASCII-коды букв А и F, измененные для проверки на нечетность

Система контроля, описанная выше, называется контролем нечетности (odd parity), так как мы построили нашу систему таким образом, что каждый код содержит нечетное число единиц. Существует также метод-антипод — контроль четности (even parity). Б таких системах каждый двоичный код содержит четное число единиц, и, следовательно, об ошибке говорит появление кода с нечетным числом единиц.

Сегодня использование контрольных разрядов четности в оперативной памяти компьютера довольно распространено. Хотя мы говорили, что ячейка памяти машин состоит из восьми битов, на самом деле она состоит из девяти битов, один из которых используется в качестве контрольного бита. Каждый раз, когда 8-битовый код передается в запоминающую схему, схема добавляет контрольный бит соответствия и сохраняет получающийся 9-битовый код. Если код уже был получен, схема проверяет его на четность. Если в нем нет ошибки, память убирает контрольный бит и возвращает 8-битовый код. В противном случае память возвращает восемь информационных битов с предупреждением о том, что возвращенный код может не совпадать с исходным кодом, помещенным в память.

Длинные двоичные коды часто сопровождает набор контрольных битов четности, которые образуют контрольный байт. Каждый разряд в байте соответствует определенной последовательности битов, находящейся в коде. Например, один контрольный бит может соответствовать каждому восьмому биту кода, начиная с первого, а другой может соответствовать каждому восьмому биту, начиная со второго. В этом случае больше вероятность обнаружить скопление ошибок в какой-либо области исходного кода, поскольку они будут находиться в области действия нескольких контрольных битов четности. Разновидностью контрольного байта являются такие схемы для обнаружения ошибок, как контрольная сумма и циклический избыточный код.

Коды с исправлением ошибок. Хотя использование контрольного разряда четности и позволяет обнаружить ошибку, но не дает возможности исправить ее. Многие удивляются тому, что коды с исправлением ошибок построены таким образом, что с их помощью можно не только найти ошибку, но и исправить ее. Интуиция подсказывает нам, что мы не сможем исправить ошибку в полученном сообщении, не зная информацию, которая в нем содержится. Однако простой корректирующий код представлен на рис. 2.

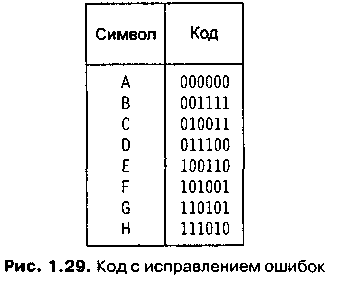
Рисунок 2 – Коды с исправлением ошибок

Для того чтобы понять, как работает этот код, определим сначала расстояние Хемминга (Hamming distance) между двумя кодами как число различающихся разрядов. Это расстояние названо в честь Р. В. Хемминга (R. W. Hamming), который первым стал исследовать коды с исправлением ошибок, поняв ненадежность релейных машин в 40-х годах XX века. Например, расстояние Хемминга между кодами символов А и В равно четырем (см. рис. 1.29), а расстояние Хемминга между В и С равно трем. Важное свойство этой системы кодирования состоит в том, что расстояние Хемминга между любыми двумя кодами больше или равно трем. Поэтому если один бит в коде будет изменен, ошибку можно будет обнаружить, так как результат не будет допустимым кодом. (Для того чтобы код выглядел, как другой допустимый код, мы должны изменить по меньшей мере три бита.)

Кроме того, если появится ошибка в коде (см. рис. 1.29), мы сможем понять, как выглядел исходный код. Расстояние Хемминга между измененным кодом и исходным будет равно единице, а между ним и другими допустимыми кодами — по меньшей мере двум. Для того чтобы расшифровать сообщение, мы просто сравниваем каждый полученный код с кодами в системе до тех пор, пока не найдем код, находящийся на расстоянии, равном единице, от исходного кода. Это и будет правильный символ. Например, предположим, что мы получили код 010100. Если мы сравним его с другими кодами, то получим таблицу расстояний (рис. 3). Следовательно, мы можем сделать вывод, что был послан символ D, так как между его кодом и полученным кодом наименьшее расстояние.

Рисунок 3 – Расшифровка кодов 010100 с использованием кодов из рисунка 2

Вы увидите, что использование этой системы (коды на рис. 2) позволяет обнаружить до двух ошибок в одном коде и исправить одну. Если мы создадим систему, в которой расстояние Хемминга между любыми двумя кодами будет равно самое меньшее пяти, мы сможем обнаружить до четырех ошибок в одном коде и исправить две. Конечно, создание эффективной системы кодов с большими расстояниями Хемминга представляет собой непростую задачу. В действительности, она является частью раздела математики, который называется алгебраической теорией кодов и входит в линейную алгебру и теорию матриц.

Методы исправления ошибок широко применяются для того, чтобы повысить надежность компьютерного оборудования. Например, они часто используются ii дисководах для магнитных дисков большой емкости, чтобы уменьшить вероятность того, что изъян на магнитной поверхности диска разрушит данные. Кроме того, главное различие между форматом первоначальных компакт-дисков, которые использовались для звукозаписей, и более поздним форматом, который используется для хранения данных в компьютере, состоит в степени исправления ошибок. Формат CD-DA включает в себя возможности исправления ошибок, которые сводят частоту появления ошибок к одной ошибке на два компакт-диска. Этого достаточно для звукозаписи, но компании, использующие компакт-диски для поставки программного обеспечения покупателям, сказали бы, что наличие дефектов в 50 процентах дисков — слишком много. Поэтому в компакт-дисках для хранения данных применяются дополнительные возможности исправления ошибок, сокращающие вероятность появления ошибки до одной ошибки на 20 000 дисков.