Домашняя самостоятельная работа №5 «Сложные суждения. Построение таблиц истинности сложных суждений»
Задание №1. Пусть а есть высказывание «9 — четное число» и b — высказывание «9 — нечетное число». Определите значения истинности следующих высказываний:
а)
а
¬b,
д) ¬a
¬b,
и) ¬a
¬b, н)
¬ (а
b),
б)
b
а,
е) ¬b
а,
к) ¬a
b,
о) ¬ (¬а
b),
в)
а
¬Ь,
ж) ¬b
¬a,
л) а
¬b,
п) ¬ (а
¬b),
г)
¬а
6,
з) а
b,
м) ¬ (а
b),
р) ¬ (¬а
¬b).
(максимальное количество баллов - 16)
Задание №2. Используя таблицы истинности для логических связок, определите истинностное значение приведенных сложных высказываний, предполагая, что а — истинное высказывание:
а) а \/ а, е) а & ¬а,
б)
а & а, ж) ¬ (а
а),
в)
а
а,
з) ¬ (а \/¬а),
г)
a
а,
и) ¬ (а & ¬а),
д)
а \/ ¬а, к) а
¬¬а.
(максимальное количество баллов - 10)
Задание №2. Укажите истинное значение приведенных в предыдущем примере сложных высказываний, предполагая, что а — ложное высказывание.
(максимальное количество баллов - 10)
Задание №3. Определите с помощью таблиц истинности, какие из приведенных формул являются тавтологиями:
а)
(a
b)
(b
a),з)
(а
b)
¬
(a & ¬b),
б)
(а &b)
(b&а),
и) (а \/ b)
(¬а
b),
в)
(а
b)
(b
а),
к) (a
\/ b)
¬
(¬а & ¬b),
г)
(а
b)&
¬b
¬a,
л) (a
& b)
¬
(¬а \/ ¬b)
,
д)
(¬а
¬b)
(b
а),
м) (а &b)
¬
(а
¬b),
e)
(а
b)
& a
b,
н)
(а
b)
&(b
a)
¬ (a
b)
ж)
(а
b)
(¬a
b),
(максимальное количество баллов -13)
Задание №4. Определите, какие из приведенных высказываний являются тавтологиями:
а) Если Иванов здоров, то он здоров и богат.
б) Если Иванов здоров, то он здоров или богат.
в) Если Иванов здоров и богат, то он здоров.
г) Если Иванов здоров или богат, то он здоров.
д) Неверно, что число делится на 2 и на 3, только если оно не делится на 2 или не делится на 3.
е) Неверно, что число является простым или четным, если и только если оно не является простым и не является четным.
(максимальное количество баллов - 6)
Задание №5. Определите, какие из приведенных высказываний логически следуют из высказывания «5 больше 3»:
а) 5 больше 3 или 3 больше 5.
б) Если 5 меньше 3, то 5 больше 3.
в) Если Париж расположен на Темзе, то 5 больше 3.
г) Неверно, что 5 больше 3 и вместе с тем 5 равно 3.
(максимальное количество баллов - 4)
Тема 4 (продолжение)
Информационный материал
Сложное высказывание будем назвать тождественно истиннымилитавтологией, если оно принимает значение истины для всех наборов значений входящих в него простых высказываний.
Два сложных высказывания будем называть равносильными, если их значения совпадают при одних и тех же наборах значений входящих в них простых высказываний.
Доказательство приведенных ниже основных равносильностей алгебры высказываний выполняется при помощи составления таблиц истинности.
Закон тождества:
;Закон непротиворечия:
;Закон исключенного третьего:
;Закон двойного отрицания:
;Законы ассоциативности:
;Законы коммутативности:
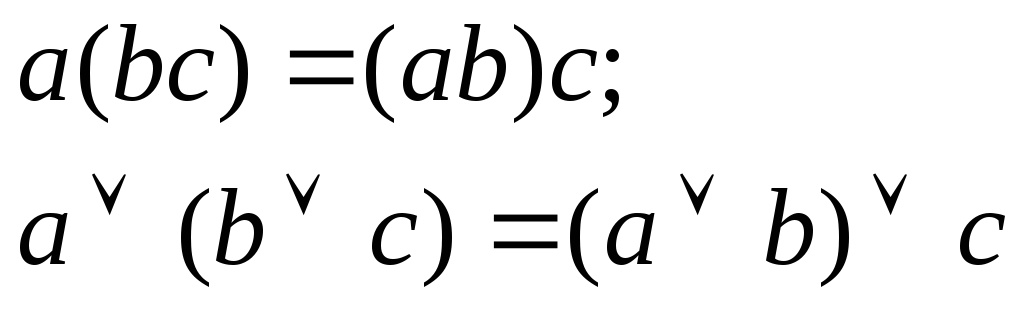;Законы дистрибутивности:
Законы поглощения:
Законы де Моргана:
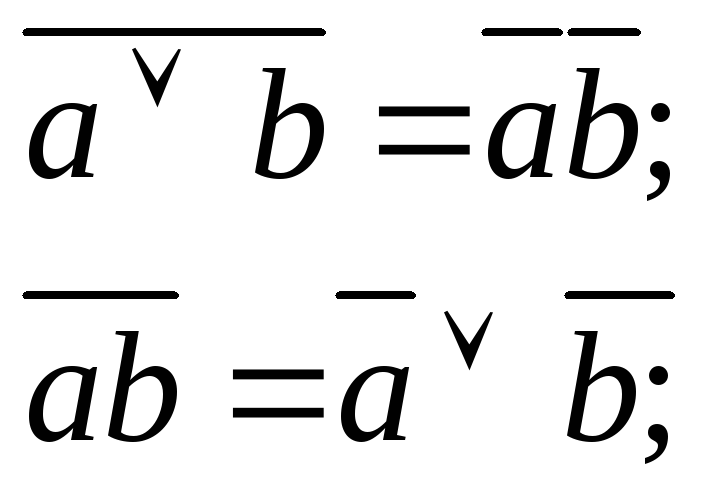
Связь конъюнкции, дизъюнкции, импликации и отрицания:
;
:
;
;
;
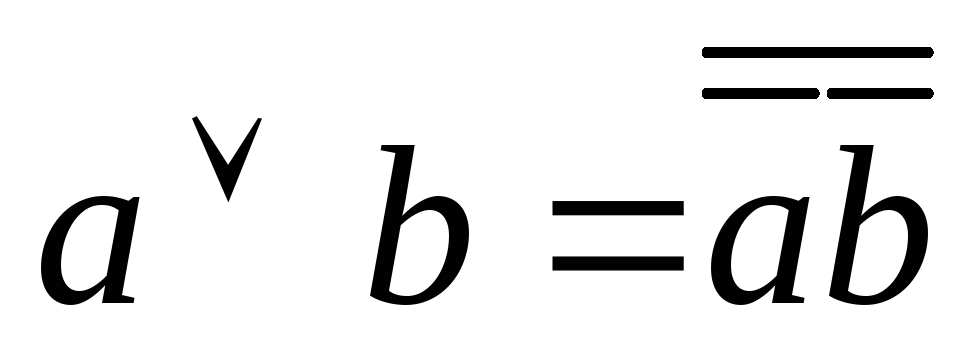;Модусы (разновидности схемы утверждений):
-утверждающий модус;
- отрицающий модус;Отрицающе-утверждающий модус:
;Законы транзитивности:
Законы контрапозиции:
Законы косвенного доказательства:
Законы Клавия:
В
качестве примера докажем, что, например,
формулы
и
являются
тождественно истинными (тавтологиями),
построив для их левых и правых частей
таблицы истинности и используя табличные
определения основных логических
операций
1.
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
В четвертом и седьмом столбцах полученной таблицы содержаться истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула является тавтологией.
2.
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
В третьем и пятом столбцах полученной таблицы содержатся истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула также является тавтологией.
Пример:
Определить с помощью таблиц истинности, является ли приведенная формула алгебры высказывание тавтологией
(а
\/ b)
(¬а
b)
|
а |
b |
¬а |
а+ b |
¬a |
(а
\/ b)
|
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
1 |
b
(¬а
b)
В последнем столбце построенной для данной формулы таблицы истинности при всех наборах значений переменных ходящих в нее простых высказываний получены только значения истины, следовательно, она является тавтологией.