
Высш мат 2014
.docxЗанятие № 1.
Тема: Производная и дифференциал функции.
Цель: 1. Повторение теоретических основ дифференцирования.
2. Приобретение практических навыков нахождения производной и дифференциала простых и сложных функций.
Краткая теория. Производной
функции
 f(x)
называется предел отношения приращения
функции y
к приращению аргумента x
в точке x при стремлении x
к нулю:
f(x)
называется предел отношения приращения
функции y
к приращению аргумента x
в точке x при стремлении x
к нулю:
 , где y
= f(x1)-f(x2),
x
= x1-x2
и
, где y
= f(x1)-f(x2),
x
= x1-x2
и
 - производная функции.
- производная функции.
Процесс нахождения производной называется дифференцированием.
Производные некоторых функций :
 (1.1)
(1.1)
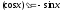 (1.8)
(1.8)
 (1.2)
(1.2)
 (1.9)
(1.9)
 (1.3)
(1.3)
 (1.10)
(1.10)
 (1.4)
(1.4)
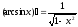 (1.11)
(1.11)
 (1.5)
(1.5)
 (1.12)
(1.12)
 (1.6)
(1.6)
 (1.13)
(1.13)
 (1.7)
(1.7)
 (1.14)
(1.14)
Правила дифференцирования:
Производная суммы (разности) функций y=u v:
 (1.15)
(1.15)
Производная произведения функций y=uv :
 (1.16)
(1.16)
Производная
частного функций
 :
:
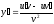 (1.17)
(1.17)
Производная сложной функции у=f(g(x)) :
 (1.18)
(1.18)
II. Дифференциал независимой переменной равен ее приращению:
dx = x (1.19)
Дифференциал функции y =f(x) :
dy =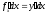 (1.20)
(1.20)
Дифференциал некоторых выражений :
d(u v)=du
v)=du dv
(1.21)
dv
(1.21)
d(uv)=vdu+udv (1.22)
d( =
= (1.23)
(1.23)
Примеры решения задач.
1).
y= -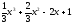 ;
;

2).
 ;
;

3).
 ;
;

Задания для самостоятельного решения и решения у доски.
Найти производные следующих функций :
1.
y=x3+2x2+8;
 =
=
2.
y=2 ;
;
 =
=
3.
y=xa+b
;
 =
=
4.
y=(1-4x3)(1+2x2);
 =
=
5.
y=2x- ;
;
 =
=
6.
y=tgx + lnx +
 ;
;
 =
=
7.
y=excosx
;
 =
=
5
-
y=
 ;
;
 =
=
-
y=
 ;
;
 =
=
-
y=e3x;
 =
=
-
y= x+sinx cosx ;
 =
=
12.
y=sin
 ;
;
 =
=
13.
y= ;
;
 =
=
14.
y= ;
;
 =
=
15.
y=ln(ecosx)
;
 =
=
16.
y= ;
;
 =
=
17.
y= ;
;
 =
=
18.
y= ;
;
 =
=
19.
y= lg3(x2);
 =
=
20.
y= ;
;
 =
=
Примеры нахождения дифференциала функции :
1.
y= ;
dy =
;
dy =
 dx
;
dx
;
 ;
dy =
;
dy =
 ;
;
2.
y= ;
;
dy=
= =
= ;
;
Найти дифференциалы следующих функций :
1). y=(2x+x2)3 ; dy=
2).
y= ;
dy=
;
dy=
3).
y= ;
dy=
;
dy=
4). y=xex-ex-2; dy=
5).
y= ;
dy=
;
dy=
Домашнее задание :
I). Найти производные функций :
1).
y=(x4-x2+1)3;
 =
=
2).
y= ;
;
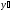 =
=
3).
y= ;
;
 =
=
4).
y= ;
;
 =
=
5).
y=sin(cos2x)cos(sin2x);
 =
=
6).
y=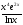 ;
;
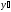 =
=
7).
y= ;
;
 =
=
II). Найти дифференциалы функций :
1).
y= ;
dy=
;
dy=
2). y=ex/2 cos x/2 ; dy=
3).
y= ;
dy=
;
dy=
Занятие №2.
Тема: Градиент функции. Основы интегрирования.
Цель: 1. Изучение основных понятий и определений. 2. Получение навыков интегрирования. 3. Освоение основных методов интегрирования.
Краткая теория. I. Говорят, что в пространстве задано поле некоторой величины, если в каждой точке пространства определено значение этой величины. Поле может быть скалярным (давление, температура, концентрация) или векторным ( скорость, сила).
Поле может быть стационарным, если оно не меняется со временем, или нестационарным в обратном случае. С формальной точки зрения стационарное поле - это функция трех переменных x, y,z :
U (x,y,z). В поле дана точка М. Возможное направление выхода из нее - l.
Производной от U по направлению l называется скорость изменения поля в этом направлении в расчете на единицу длины :

l
l
Эту производную можно записать :

Правую часть удобно записать в виде скалярного произведения двух векторов :

Первый из них называется градиентом поля :
grad
U =
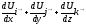 (2.1)
(2.1)
Второй вектор :

называется единичным вектором направления l.
Вектор grad U в точке М всегда указывает в сторону наибыстрейшего возрастания поля U.
II. Функция F(x) , имеющая данную функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции f(x).
Например: f(x)=cos x F(x)=sin x
f(x)= x2 F(x)=x3/ 3
Совокупность
всех первообразных функций для
дифференциала f(x) dx называется
неопределенным интегралом и обозначается
:
 = F(x) + C.
= F(x) + C.
Основные интегралы:
1). ,
(n
-1) (2.2); 5).
,
(n
-1) (2.2); 5). sin
x dx= - cos x + C , (2.6);
sin
x dx= - cos x + C , (2.6);
2). x
+ C , (2.3);
6).
x
+ C , (2.3);
6). cosx
dx= sin x + C , (2.7);
cosx
dx= sin x + C , (2.7);
3). , (2.4);
7).
, (2.4);
7). tg x + C , (2.8);
tg x + C , (2.8);
4). ex
dx= ex
+ C , (2.5);
8).
ex
dx= ex
+ C , (2.5);
8). - ctg x + C , (2.9).
- ctg x + C , (2.9).
Основные методы интегрирования.
1. Метод замены переменной.
Если
 (t)
= f(t) и t=
(x) , то
(t)
= f(t) и t=
(x) , то
 F((x))
+ C.
F((x))
+ C.
Например :
 d(2x
- 5)=2dx =
d(2x
- 5)=2dx = =
=
=

2. Интегрирование подстановкой.
Рассмотрим на примере :

Пусть: 1 - x =t и x=1- t . Дифференцируя имеем: dx= - dt . Тогда:
 -
-
=
-
 .
.
3. Интегрирование по частям.
 UdV=UV
-
UdV=UV
-
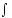 VdU
VdU
Пример :
 x
sinx dx=
x
sinx dx=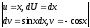 =
- x cosx -
=
- x cosx -
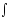 (-cosx)dx=
- x
cosx+sin
x + C .
(-cosx)dx=
- x
cosx+sin
x + C .
Задания для самостоятельного решения и решения у доски.
1). Найти интегралы методом замены переменной.
1).
 =
=
2).
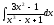 =
=
3).
 =
=
4).
 =
=
5).
 =
=
2). Проинтегрировать методом подстановки:
1.
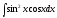 =
=
2.
 =
=
3.
 =
=
4.
 =
=
5.
 =
=
1.
 =
=
2.
 =
=
3.
 =
=
4.
 =
=
5.
 =
=
4). Найдите интегралы:
1.
 =
=
2.
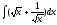 =
=
3.
 =
=
4.
 =
=
5.
 =
=
6.
 =
=
Домашнее задание.
Вычислить интегралы:
1.
 =
=
2.
 =
=
3.
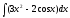 =
=
15
3). Проинтегрировать по частям.
4.
 =
=
5.
 =
=
6.
 =
=
7.
 =
=
8.
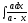 =
=
9.
 =
=
10.
 =
=
Занятие № 3.
Тема: Определенный интеграл. Дифференциальные уравнения.
Цель: 1. Освоение нового материала, повторение ранее изученного.2. Приобретение практических навыков вычисления определенного интеграла и решения дифференциальных линейных уравнений.
Краткая теория.
1. Формула Ньютона- Лейбница:
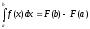 , где (3.1)
, где (3.1)
F(x)
- первообразная функции f(x) , т.е.
 .
.
Свойства определенного интеграла:
 ;
(3.2)
;
(3.2)
 (3.3)
(3.3)
 (3.4)
(3.4)
Примеры решения :
1.
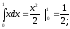
2.

3.
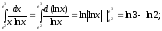
4.
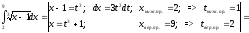
= .
.
Обратите внимание, при подстановке пределы интегрирования меняются.
Для вычисления определенного интеграла используются те же методы, что для нахождения неопределенного.
5). Вычислим площадь фигуры, ограниченной линиями :
y=2x - x2 и y=x.
Нужно найти пределы интегрирования a и b. Для этого нужно решить уравнение :
2x - x2 = x
x - x2 = x2 - x = 0
x(x - 1) = 0
x1 = 0 = a
x2 = 1 = b
S=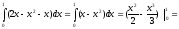 =1/2 - 1/3 = 1/6 .
=1/2 - 1/3 = 1/6 .
II. Общий вид дифференциального уравнения :
F(x, y,
 (3.7)
(3.7)
Общее решение дифференциального уравнения :
y=f( x, C1, C2, . . . , Cn) . (3.8)
Общий вид дифференциального уравнения первого порядка :
 (3.9)
(3.9)
Общее решение дифференциального уравнения первого порядка :
y=f(x , C ). (3.10)
1).
Дифференциальное уравнение типа
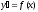 :
:
 dy=f(x) dx
dy=f(x) dx
Общее
решение : y= f(x)dx=F(x)
+ C.
f(x)dx=F(x)
+ C.
2).
Дифференциальное уравнение типа
 :
:
 ;
;

Общее
решение :

3). Дифференциальное уравнение с разделенными переменными :
f(x) dx + (y) dy = 0
Общее
решение :
F(x) + (y) = C.
4). Дифференциальное уравнение с разделяющимися переменными:
f(x) (y) dx + (x) Ф(y) dy = 0.
Приведем уравнение к уравнению с разделенными переменными:

Общее решение :
 или F1
(x) + F2
(y) = C.
или F1
(x) + F2
(y) = C.
Примеры решения :
1). Является ли решением данного дифференциального уравнения указанная функция ?
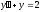 , y=x ex
, y=x ex
Для этого продифференцируем функцию два раза и подставим в исходное уравнение ее вторую производную и саму функцию . Если тождество окажется верным, значит приведенная функция является решением уравнения .
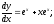
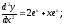 это
это

Подставляем в уравнение
y и
 :
:
2 ex + x ex + x ex = 2 ex + 2 x ex 2
Таким образом, данная функция не является решением приведенного дифференциального уравнения.
2). Найдем общее решение дифференциального уравнения :


Разделим переменные :


Интегрируем обе части уравнения :
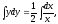

y2 = ln x + C ,
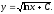 - общее решение.
- общее решение.
Задания для самостоятельного решения и решения у доски.
1). Вычислите интегралы:
1.
 =
=
2.
 =
=
3.
 =
=
4.
 =
=
5.
 =
=
6.
 =
=
7.
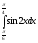 =
=
8.
 =
=
9.
 =
=
21
10.
 =
=
2. Выясните, является ли решениями данных дифференциальных уравнений указанные функции :
1.

2.

3.

4.

5. (x+2)dx - 2 dy = 0 , y=x2 / 4 + x .
3. Найдите общее решение следующих дифференциальных уравнений :
1.

2. (x + 1 ) dx - 2 xy dy = 0 ;
3. x dx = y dy ;
4.

5.
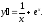
Домашнее задание :
1. Вычислить интегралы :
1).
 =
=
2).
 =
=
3).
 =
=
4).
 =
=
23
5).

2. Являются ли решениями данных дифференциальных уравнений приведенные функции
1)

2)

3)

3. Найти общее решение :
1)
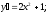
2)

3) dy + 3y dx = 0.
