Математические модели являются инструментальным средством описания задач самого разного класса. Причем задачи из разных областей экономики могут иметь похожие модели и решаться одинаковыми методами. Использование корректно-построенной модели какого-либо процесса позволяет формализовать и описать наиболее важные связи между объектами, оценить различные параметры зависимостей, предсказывать поведение объекта, тем самым определять наилучшие решения в той или иной ситуации, оценить количественно эффективность принимаемых решений, прогнозировать их негативные последствия, использовать полученные оценки.

Математическая модель – это условный совокупный образ объекта в виде совокупности уравнений, неравенств, логических соотношений, созданный для получения новых знаний, исследования объекта, анализа и оценки принимаемых решений в конкретных или возможных ситуациях.

Моделирование – это метод исследования объектов, процессов на их моделях, построение и изучение моделей, определения и улучшения их характеристик, рацион6ализирующих способ построения и управления.

В разных науках существуют различные способы классификации моделей. Классификация зависит от признака, лежащего в основе. Признаком может выступать отрасль знаний, способ представления модели, учет временного фактора, приспособляемости модели.

По отраслям знаний модели классифицируются на биологические, социологические, физические, экономические.

Математические модели, используемые в экономике, можно классифицировать по особенностям моделируемого объекта – на макро- и микроэкономические; по целям моделирования и используемому инструментарию – на теоретические и прикладные, оптимизационные и равновесные, статические и динамические, непрерывные и дискретные, стохастические и детерминированные.

Макроэкономические модели описывают экономику страны как единое целое, связывая такие макроэкономические материальные и финансовые показатели, как ВВП, потребление, инвестиции, занятость, бюджет, инфляция, ценообразование и др.

Микроэкономические модели описывают состояние структурных составляющих экономики, стратегии поведения фирм в неустойчивой или стабильной среде.

Прикладные модели обеспечивают возможность оценки параметров функционирования конкретных технико-экономических объектов и обоснования выводов для принятия управленческих решений. Равновесные модели, присуще рыночной экономике, описывают поведение субъектов хозяйствования в стабильных устойчивых состояниях, но и в нерыночной экономике, где равновесие по одним параметрам компенсируется другими факторами.

По назначению: балансовые (наличие ресурсов и их использование), трендовые (развитие моделируемой системы через тенденцию развития ее показателей), оптимизационные, имитационные (машинная имитация процессов). Оптимизационные модели связаны в основном с микроуровнем и предполагают выбор наилучшего варианта (максимум прибыли, минимум расходов и т.д.) по некоторому критерию, причем различают одно- и многокритериальные задачи.

Статические модели описывают состояние объекта в конкретный текущий момент или период времени, а динамические модели включают взаимосвязи переменных во времени. Детерминированные модели предполагают жесткие функциональные связи между переменными, а стохастические модели допускают наличие случайности, используя в качестве инструмента теорию вероятностей и математическую статистику.

По приспособляемости: адаптивные или нет. По способу представления: предметные и знаковые. Предметные модели воспроизводят определенные геометрические, физические, динамические свойства объекта (глобус, карты..). Знаковые модели – это схемы, чертежи, формулы. Важнейшим видом знаковых моделей являются математические.

Применительно к техническим и естественным наукам принято различать следующие виды моделирования:

- концептуальное, при котором совокупность уже известных фактов и представлений о системе представляется с помощью специальных знаков, символов

- физическое моделирование, между объектом и оригиналом устанавливаются отношения подобия

- структуно-функциональное, при котором моделями являются чертежи, диаграммы, таблицы, дополненные специальными правилами их преобразования и объединения

- математическое, где модель строится средствами математики и логики

- имитационное моделирование, при котором математическая модель объекта представляет собой способ функционирования объекта, реализованный в виде программы на ПК.

Эти виды не являются взаимо-исключающими и могут применяться в комбинации.

Примерами программных продуктов структурно-функционального моделирования являются программные системы комплексной автоматизации предпроектного анализа и проектирования информационных систем (Bpwin, CASE-аналитик).

Инструментальные средства имитационного моделирования подразделяются на три группы:

• языки имитационного моделирования непрерывных динамических систем (как правило, с помощью дифуравнений) DINAMO, СИМФОР

• языки имитационного моделирования дискретных систем (GPSS – General Purpose Simulation System)

• универсальные языки (идея объединить достоинства GPSS и DINAMO

Перспективным направлением развития является язык UML (Unified Modeling Language)

Основные задачи управления деятельностью человека можно отнести к классу задач распределения и оптимизации ресурсов. Например, технологический процесс можно определить как последовательность работ, которые определяют превращение сырья в продукцию, такую последовательность работ называют маршрутом, каждую операцию, входящую в маршрут, можно охарактеризовать определенными режимами обработки, управления, контроля и функционирования. Процессы функционирования объекта и технологические процессы характеризуются изменениями некоторых параметров во времени, они подразделяются на дискретные и непрерывные. Зависимости между переменными и целевые функции могут быть линейными и нелинейными.

Итак, если выделить в модели следующие элементы: исходные данные, зависимости, описывающие целевую функцию, ограничения, то типы математических моделей могут быть представлены схемой (рис.1.2.1).

Рис. 1.2.1 Разновидности элементов математической модели.

Процесс построения и исследования компьютерной модели можно представить как последовательность следующих шагов:

1. Знакомство с предметной областью, прогноз или анализ процесса. Формулировка целей моделирование, уточнение круга задач. Предварительная оценка целесообразности построения модели.

2. Переход от описания предметной области в содержательных терминах к формализованным описаниям. Введение переменных, установления связей между объектами в виде формального текста. Выбор алгоритма, технологии решения задачи.

3. Выбор специального программного и аппаратного обеспечения. Реализация разработанной модели программно-аппаратными средствами.

4. Анализ построенной модели, оценка адекватности модели, экспертный анализ. Работа с готовой моделью, выдвижение гипотез, альтернативных вариантов. Принятие решений, разработка планов действий, контроль над реализацией плана.

В каждой задаче мы должны ясно определить цели, поставленные перед системой, изучить обстановку, освоиться с терминологией, процессом, определить различные способы действия, приемлемые для ситуации, дать в какой-то форме постановку задачи. Построить подходящую логическую, или математическую модель, которая свяжет переменные задачи с реальными ограничениями, целями задачи, мерой эффективности. Затем, исходя из полученной модели, выбрать метод, и найти решение, оптимизирующее эту меру эффективности, т. е. оптимальное решение. И сравнить это полученное с помощью математической модели решение с действительностью, чтобы выяснить, в самом ли деле мы сформулировали и решали ту реальную задачу, с которой начали? Когда меняется ситуация, какие изменения надо вносить в математическую модель? Можно ли улучшить модель, что привело бы к новым решениям, более реалистичным и точным. Рассмотрим задачи стохастического моделирования с элементом случайности.

2.1 Имитационное моделирование экономическиХ систем с использованием марковских случайных процессов

Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной.

Случайная функция X(t), аргументом которой является время, называется случайным процессом.

Марковские прcцессы являются частным видом случайных про­цессов. Особое место марковских проuессов среди других классов случайных процессов обусловлено следующими обстоятельствами: для марковских процессов хорошо разработан математический ап­парат, позволяющий решать многие практические задачи; с помо­щью марковских процессов можно описать (точно или приближен­но) поведение достаточно сложных систем.

Определение. Случайный процесс, протекающий в какой-либо системе S, называется марковским (или процессом без последейст­вия), если он обладает следующим свойством: для любого момента времени t₀ вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, когда и каким образом система S пришла в это со­стояние.

Классификация марковских процессов. Классификация марковских случайных процессов производится в зависимости от непре­рывности или дискретности множесtва значений функции X(t) и параметра t. Различают следующие основные виды марковских случай­ных процессов:

- с дискретными состояниями и дискретным временем (цепь Маркова);

- с непрерывными состояниями и дискретным временем (марков­ские последовательности);

- с дискретными состояниями и непрерывным временем (непре­рывная цепь Маркова);

- с непрерывным состоянием и непрерывным временем

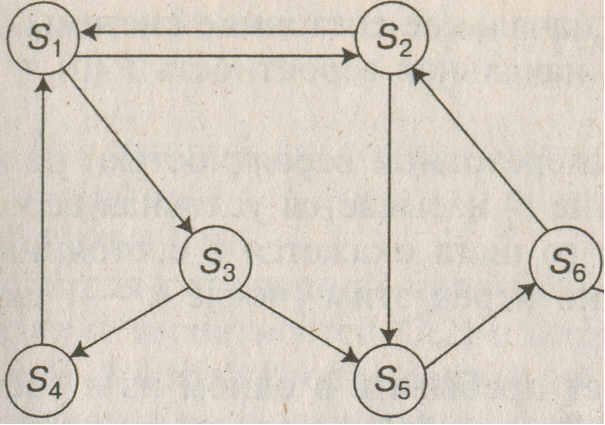
Мы будем рассматривать только марковские процессы с дискретными состояниями S₁, S₂, ..., S_n

Граф состоянии. Марковские процессы с дискретными состо­яниями удобно иллюстрировать с помощью так называемого гра­фа состояний (рис. 2.1), где кружками обозначены состояния SI, S2, ... системы S, а стрелками - возможные переходы из состо­яния в состояние. На графе отмечаются только непосредственные переходы, а не переходы через другие состояния. Возможные за­держки в прежнем состоянии изображают «петлей», т. е. стрел­кой, направленной из данного состояния в него же. Число состо­яний системы может быть как конечным, так и бесконечным (носчетным). Пример графа состояний системы S представлен нарис.2.1.

2.2 МАРКОВСКИЕ ЦЕПИ

п

~ P;(k) = 1.

i=1

(2.1)

(2.2)

п

~ P;(k) = 1.

i=1

(2.1)

Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью. Для такого процесса моменты t₁,t₂..., когда система S может менять свое со­стояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не вре­мя t, а номер шага 1, 2, ..., k, ... Случайный процесс в этом случае характеризуется последовательностью состояний S(O), S(I), S(2), ..., S(k), ..., где S(O) - начальное состояние системы (перед первым шагом); S(1) - состояние системы после первого шага.

Событие {S(k) = Si}, состоящее в том, что сразу после k-ro ша­га система находится в состоянии Si(i = 1, 2, ...), является случай­ным событием. Последовательность состояний S(O), S(I), ..., S(k), ... можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния Si в любое S. не зависит от того, когда и как система пришла в состояние S_j.

Вероятностями состояний цепи Маркова называются вероятно­сти Pi(k) того, что после k-гo шага (и до (k + 1 )-го) система S будет находиться в состоянии Si (i = 1, 2, ..., п).

Понятно, что для каждого k:

Начальным распределением вероятностей Марковской цепи называется распределение вероятностей в момент t=0: P₁(0), P₂ (0), …,P_n(0). В частном случае, если S(0)=S_i, то P_i(0)=1, а остальные равны 0.

Вероятностью перехода из состояния S_i в состояние S_j (переходной вероятностью) называется вероятность того, что система окажется в состоянии S_j, при условии , что до этого она находилась в состоянии S_i. Поскольку система может пребывать в одном из n состояний, до для каждого момента надо задать n² вероятностей, которые записывают в матрицу переходных вероятностей:

Если переходные вероятности не зависят от номера шага (от времени), а зависят только от того, из какого состояния осуществляется переход, то соответствующая цепь называется однородной.

Отметим особенности переходной матрицы:

- каждая строка характеризует выбранное состояние системы, и ее элементы – это вероятности переходов за один шаг из этого состояния в любое другое и в само себя

- элементы столбцов показывают вероятности переходов из любого состояния в конкретное,

- сумма вероятностей каждой строки равна единице, т.к. переходы образуют полную группу несовместных событий,

- по главной диагонали стоят вероятности того, что система не выйдет, а останется в прежнем состоянии.

Если для однородной марковской цепи заданы начальное распределение вероятностей и матрица переходных вероятностей известна, то вероятности состояний системы Pi(k)определяются по формуле:

Рассмотрим пример:

Рассмотрим процесс функционирования системы ­– автомобиль. Пусть автомобиль (система) в течение одной смены (суток) может находиться в одном из двух состояний: исправном (SI) и неисправном (S2). Граф состояний системы представлен на рисунке.

P₁₁=0,8 P₁₂=0,2 P₂₁=0,9 P₂₂=0,1. Матрица переходных вероятностей имеет вид:

где P₁₁ = 0,8 - вероятность того, автомобиль останется в исправном состоянии;

P₁₂ = 0,2 - вероятность перехода автомобиля из состояния «испра вен» в состояние «неисправен»;

Р₂₁ = 0,9 - вероятность перехода автомобиля из состояния «неиспра­вен» в состояние «исправен»;

Р₂₂ = 0,1 - вероятность того, что автомобиль останется в состоянии «неисправен».

Начальные вероятности состояния автомобиля заданы P₁(0)=0, P₂(0)=1. Тогда,

P₁(1)=P₁(0) P₁₁+P₂(0) P₂₁= 0,9

P₂(1)= P₁(0) P₁₂+ P₂(0) P₂₂=0,1

В момент времени t=2:

P₁(2)=P₁(1) P₁₁+P₂(1)P₂₁=0,9*0,8+0,1*0,9=0,81

P₂(2)=P₁(1) P₁₂+P₂(1) P₂₂=0,9*0,2+0,1*0,1=0,19

В момент времени t=3:

P₁(3)= P₁(2) P₁₁+P₂(2)P₂₁ =0,819,

P₂(3)= P₁(2) P₁₁+P₂(2)P₂₁ =0,181

Т.е. после трех суток автомобиль будет находиться в состоянии «исправен» с вероятностью 0,819 ,а «неисправен» с вероятностью 0,181 .