
вопросы по линейной алгебре
.docВопросы по линейной алгебре.
1. Система линейных алгебраических уравнений называется совместной, если
А) она не имеет ни одного решения;
Б) она имеет хотя бы одно решение;
В) если свободные члены этой системы равны нулю;
Г) если ранг матрицы этой системы равен 1.
2. Система линейных алгебраических уравнений называется несовместной, если
А) она не имеет ни одного решения;
Б) она имеет хотя бы одно решение;
В) если свободные члены этой системы равны нулю;
Г) если ранг матрицы этой системы равен 1.
3. Система линейных алгебраических уравнений называется определенной,
если:
А) ранг этой системы равен 1;
Б) если она имеет единственное решение;
В) если она имеет более одного решения;
Г) если она не имеет решений.
4. Система линейных алгебраических уравнений называется неопределенной, если
А) ранг этой системы равен 1;
Б) если она имеет единственное решение;
В) если она имеет более одного решения;
Г) если она не имеет решений.
5. Теорема
Кронекера-Капелли гласит: система
линейных алгебраических уравнений
![]() совместна тогда и только тогда, когда
совместна тогда и только тогда, когда
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() ;
;
Г)
![]() .
.
6. Пусть дана система
линейных алгебраических уравнений
![]() и
и
![]() где n-число
неизвестных системы. Тогда:
где n-число
неизвестных системы. Тогда:
А) система не определена;
Б) система совместна и определена;
В) система однородная;
Г) система совместна и не определена.
7. Пусть дана система
линейных алгебраических уравнений
![]() и
и
![]() где n-число
неизвестных системы. Тогда:
где n-число
неизвестных системы. Тогда:
А) система не определена;
Б) система совместна и определена;
В) система однородная;
Г) система совместна и не определена.
8. Система линейных
алгебраических уравнений
![]() несовместна тогда, когда:
несовместна тогда, когда:
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() .
.
9. Система линейных алгебраических уравнений называется неопределенной, если
А) ранг этой системы равен 1;
Б) если она имеет единственное решение;
В) если она имеет более одного решения;
Г) если она не имеет решений.
10. Если А
и В- квадратные
матрицы второго порядка, А-невырожденная,
то решение уравнения
![]() находится по формуле:
находится по формуле:
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() ;
;
Г)
![]() .
.
11. Три вектора в пространстве называются компланарными, если они:
А) лежат в одной плоскости или на параллельных;
Б) параллельны друг другу;
В) имеют одинаковую длину и параллельны друг другу.
12. Два вектора
![]() и
и
![]() называются коллинеарными, если они
называются коллинеарными, если они
А) лежат в одной плоскости или на параллельных;
Б) лежат на одной прямой или на параллельных прямых;
В) имеют одинаковую длину и параллельны друг другу;
13. Два вектора
![]() и
и
![]() называются равными, если они
называются равными, если они
А) коллинеарные, имеют одинаковую длину и направление;
Б) имеют одинаковую длину;
В) имеют одинаковую длину и коллинеарные;
Г) имеют одинаковую длину и лежат в одной плоскости.
14. Скалярное
произведение двух векторов
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() ;
;
Г)
![]() .
.
15. Косинус угла
между векторами
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
А)
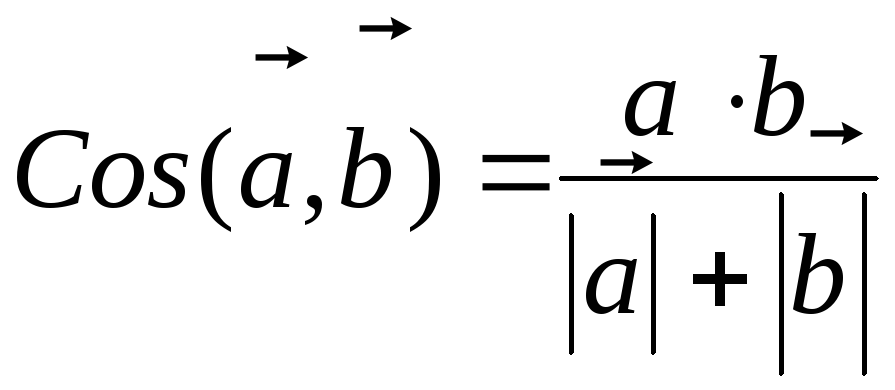 ;
;
Б)
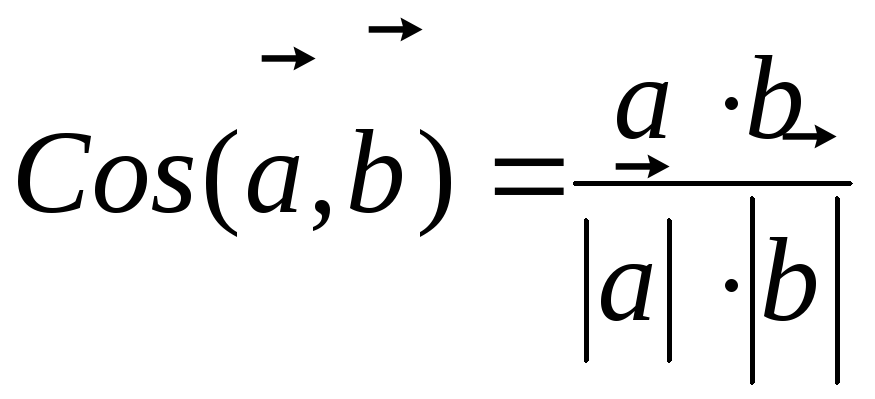 ;
;
В)
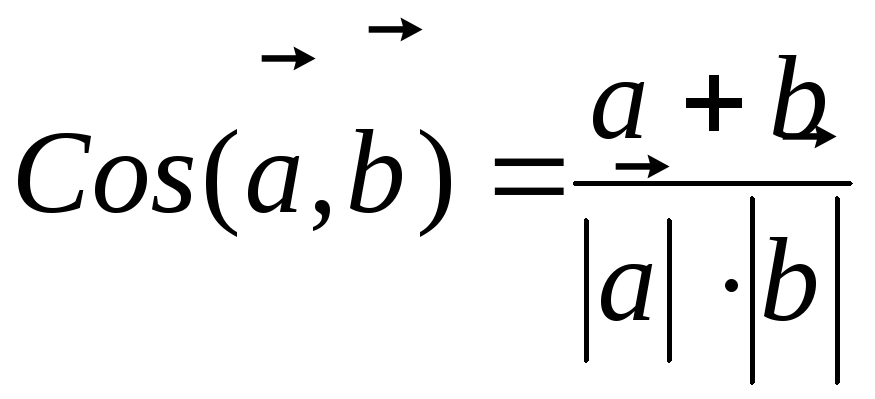 .
.
16. Векторным
произведением двух векторов
![]() и
и
![]() называется:
называется:
А) третий вектор
![]() ,
длина которого численно равна площади
параллелограмма, построенного на
векторах
,
длина которого численно равна площади
параллелограмма, построенного на
векторах
![]() и
и
![]() как на сторонах, направленный
перпендикулярно плоскости, образованной
векторами
как на сторонах, направленный
перпендикулярно плоскости, образованной
векторами
![]() и
и
![]() и причем, так, что если смотреть из конца
вектора
и причем, так, что если смотреть из конца
вектора
![]() ,
то поворот вектора
,
то поворот вектора
![]() к вектору
к вектору
![]() будет происходить против часовой стрелки
и кратчайшим путем.
будет происходить против часовой стрелки
и кратчайшим путем.
Б) третий вектор
![]() ,
и равный площади треугольника, построенного
на векторах
,
и равный площади треугольника, построенного
на векторах
![]() и
и
![]() .
.
В) третий вектор
![]() ,
длина которого равна объему пирамиды,
построенной на векторах
,
длина которого равна объему пирамиды,
построенной на векторах
![]() ,
,
![]() и
и
![]() .
.
17. Формула вычисления
векторного произведения вектора
![]() =
=![]() на вектор
на вектор
![]() =
=![]() имеет вид:
имеет вид:
А)
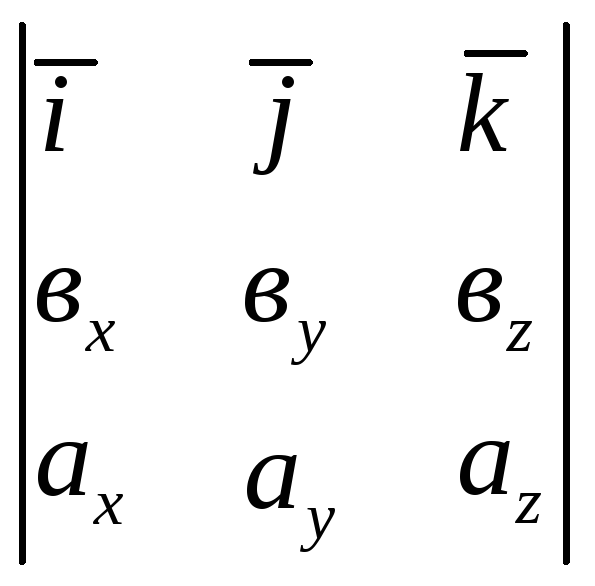 ;
;
Б)
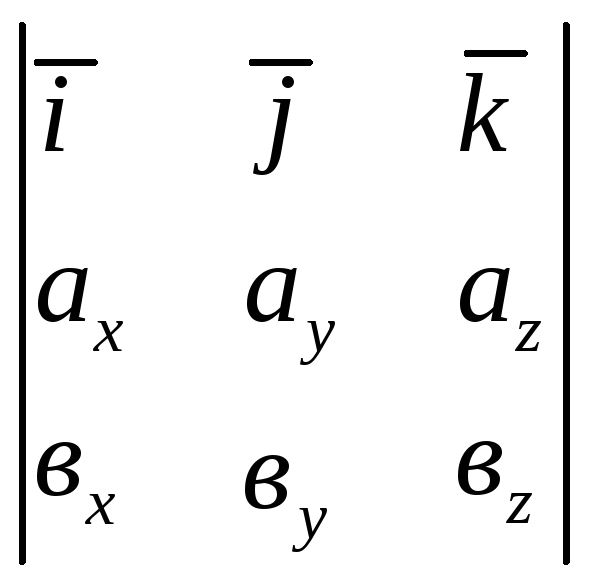 ;
;
В)
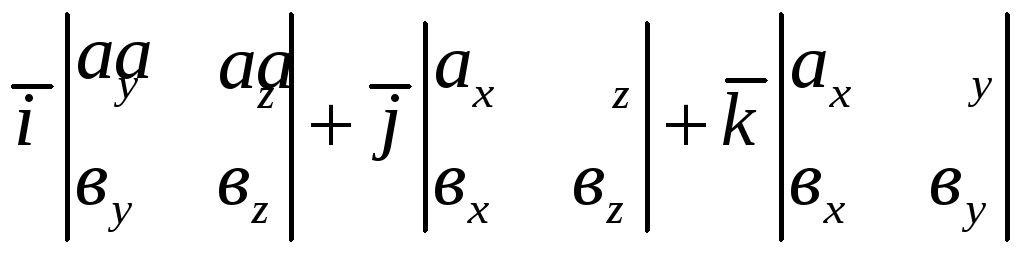 ;
;
Г)
![]() .
.
18. Если вектора
![]() =
=![]() и
и
![]() =
=![]() коллинеарные, то справедливы следующие
соотношения:
коллинеарные, то справедливы следующие
соотношения:
А)
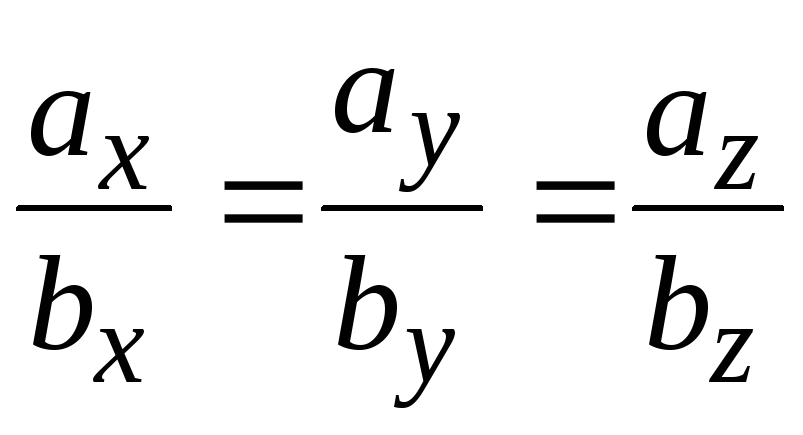 ;
;
Б)
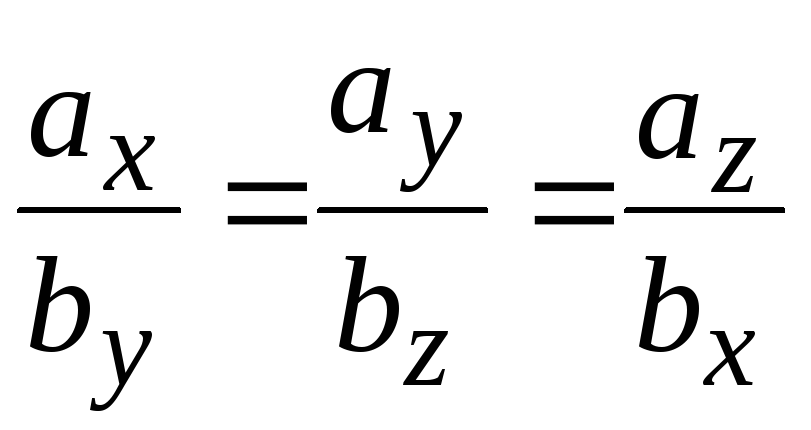 ;
;
В)
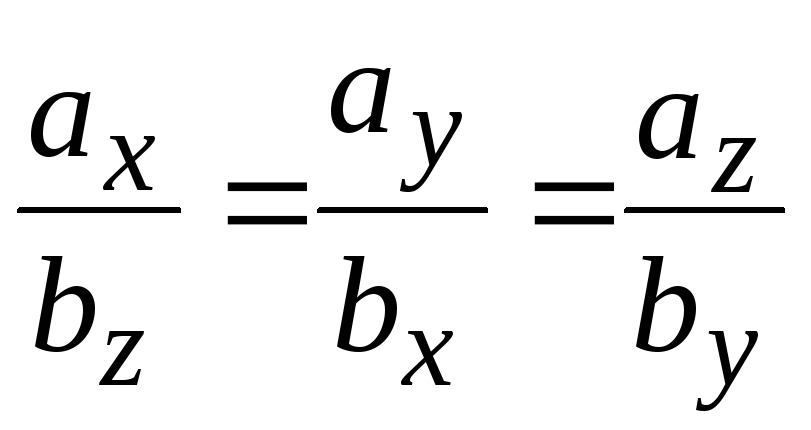 .
.
19. Смешанным
произведением трех векторов
![]() ,
,
![]() и
и
![]() называется:
называется:
А) скалярное
произведение векторного произведения
векторов
![]() и
и
![]() на вектор
на вектор
![]() ;
;
Б) скалярное
произведение суммы векторов
![]() и
и
![]() на вектор
на вектор
![]() ;
;
В) векторное
произведение вектора
![]() на сумму векторов
на сумму векторов
![]() и
и
![]() ;
;
Г) скалярное
произведение вектора
![]() на сумму векторов
на сумму векторов
![]() и
и
![]() .
.
20. Смешанное
произведение трех векторов
![]() ,
,
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
А)
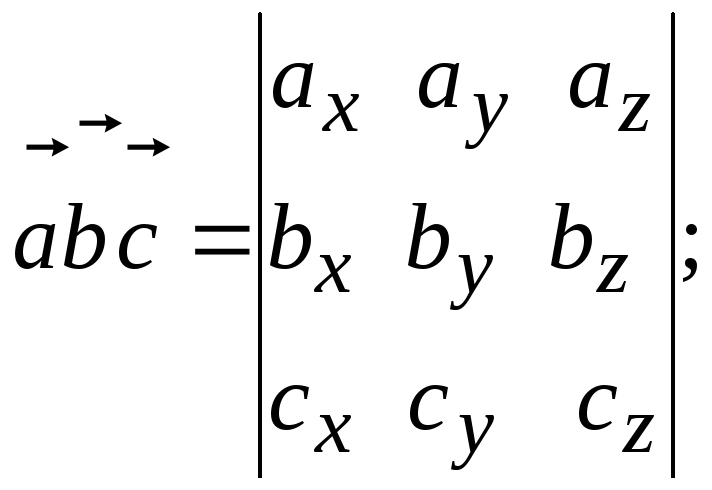
Б)
![]()
В)
![]() .
.
21. Геометрический смысл смешанного произведения трех векторов заключается в том, что оно равно:
А) длине диагонали параллелепипеда, построенного на этих векторах;
Б) объему параллелепипеда, построенного на этих векторах;
В) длине вектора, равного сумме этих трех векторов;
Г) площади параллелограмма, построенного на двух векторах перпендикулярно третьему вектору.
22. Формула вычисления объема треугольной пирамиды имеет вид:
А)
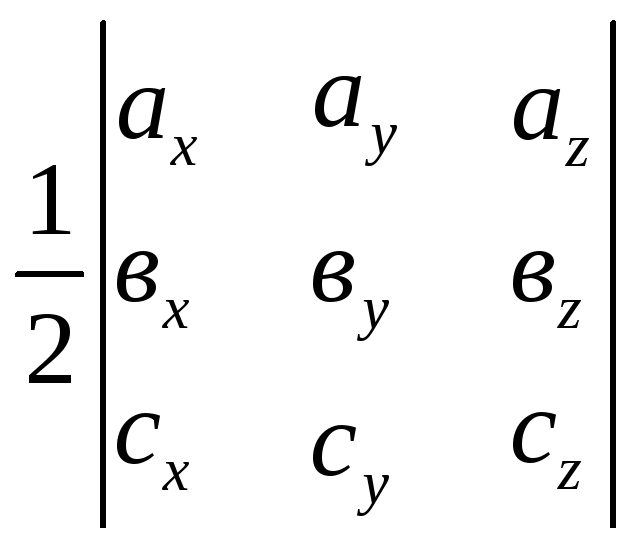 ;
;
Б)
![]()
![]()
![]() ;
;
В)
![]()
![]()
![]() ;
;
Г)
![]() .
.
23. Угол между
прямыми
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
А)
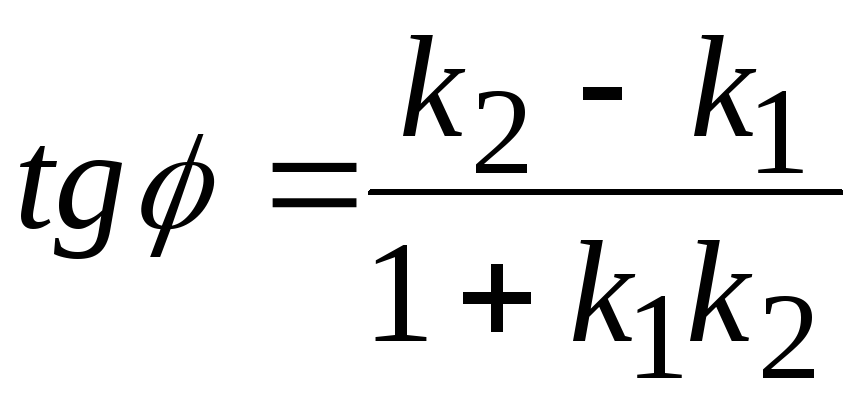 ;
;
Б)
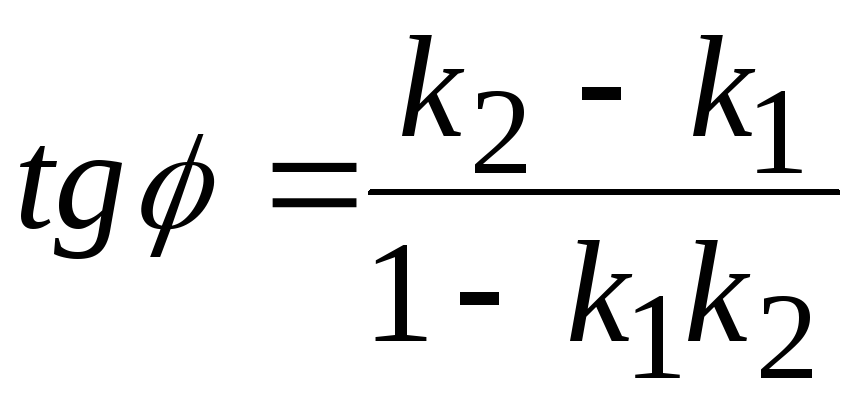 ;
;
В)
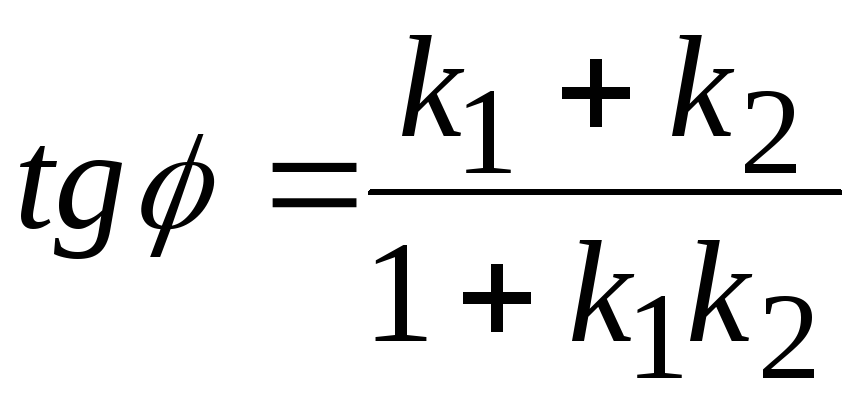 .
.
24. Если прямые
![]() и
и
![]() перпендикулярны, то выполняется следующее
равенство:
перпендикулярны, то выполняется следующее
равенство:
А)
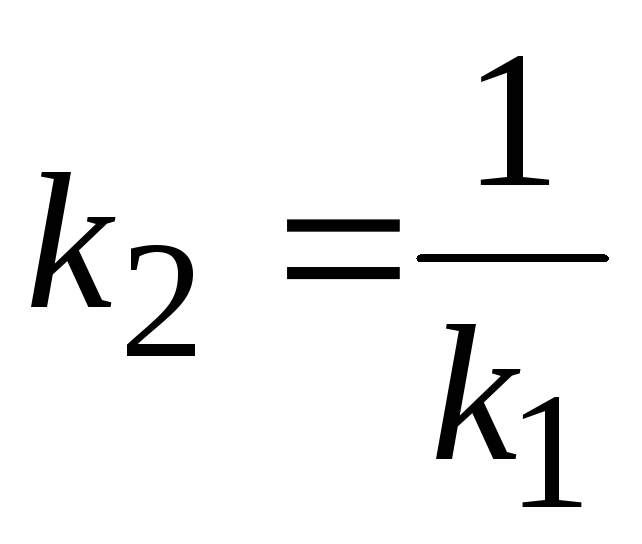 ;
;
Б)
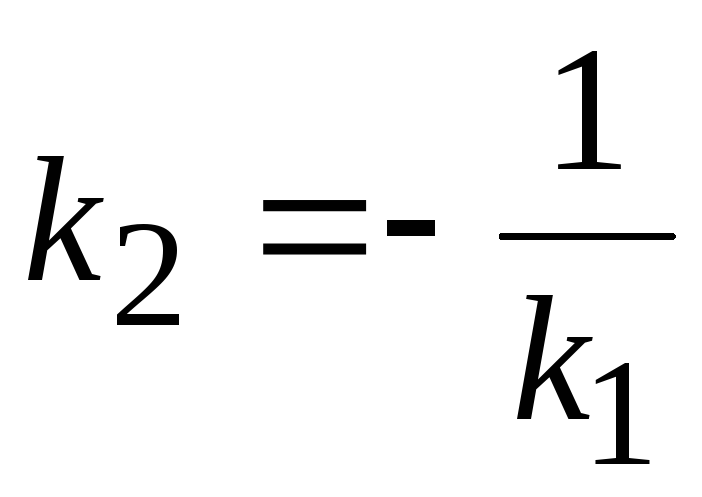 ;
;
В)
![]() .
.
25. Если прямые
![]() и
и
![]() параллельны, то выполняется следующее
равенство:
параллельны, то выполняется следующее
равенство:
А)
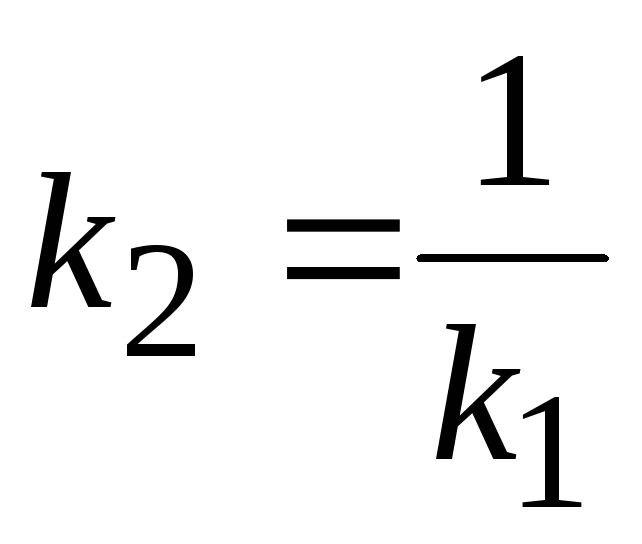 ;
;
Б)
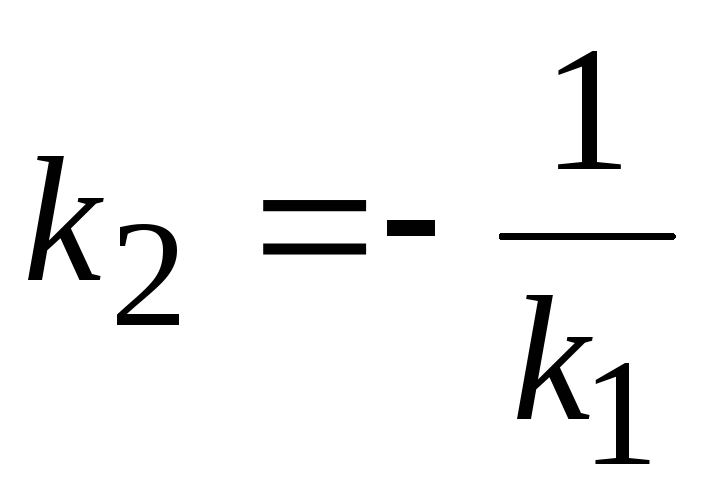 ;
;
В)
![]() .
.
26. Расстояние от
точки
![]() до прямой
до прямой
![]() вычисляется по формуле:
вычисляется по формуле:
А)
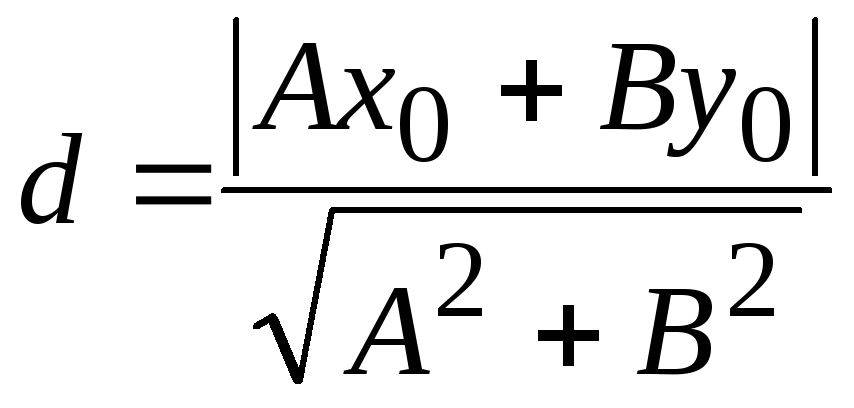 ;
;
Б)
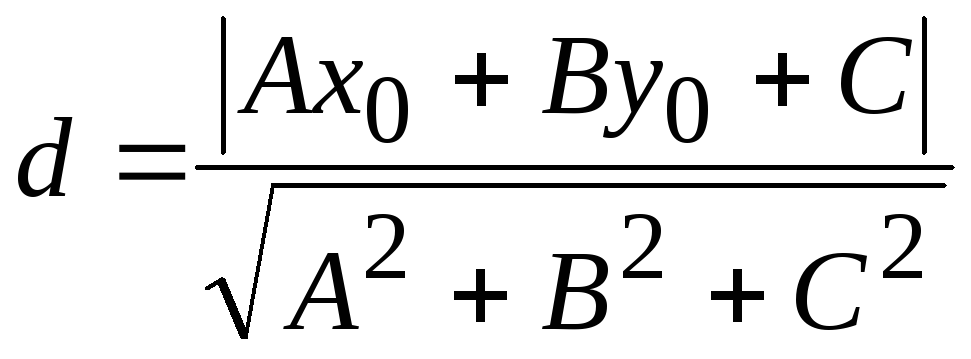 ;
;
В)
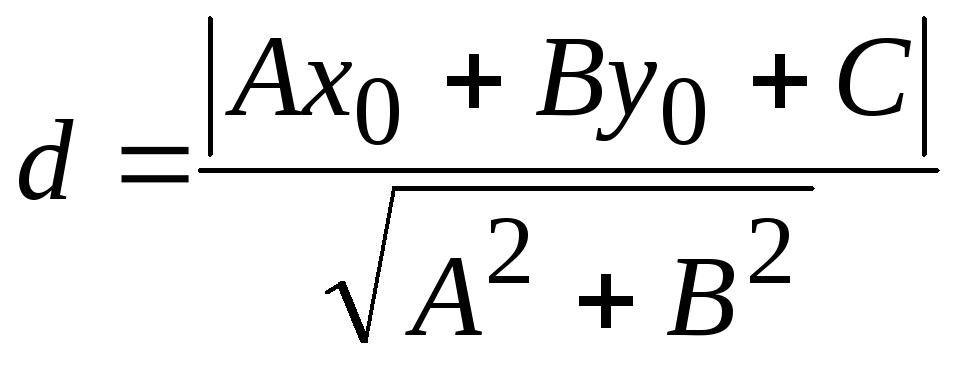 .
.
27. Уравнения
асимптот гиперболы
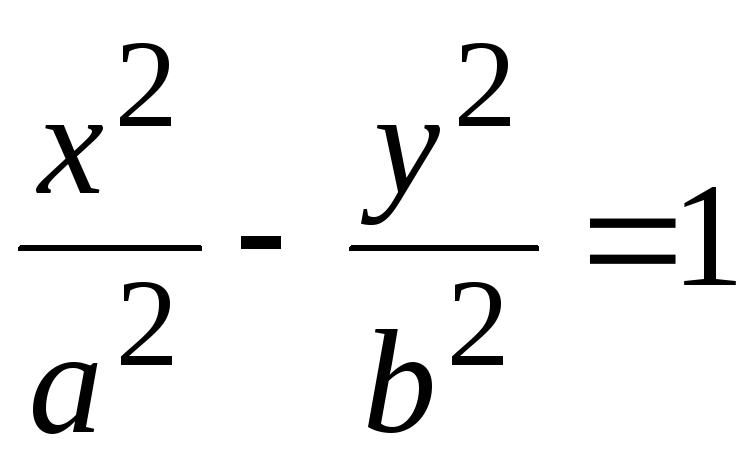 имеют вид:
имеют вид:
А)
![]()
Б)
![]()
В)
![]()
28. Уравнение
плоскости, проходящей через данную
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() имеет вид:
имеет вид:
А)
![]()
Б)
![]()
В)
![]()
29. Выберите верное утверждение:
A)
Если уравнение плоскости имеет вид
![]() то она проходит через начало координат;
то она проходит через начало координат;
Б) Если уравнение
плоскости имеет вид
![]() то она проходит через ось
то она проходит через ось
![]()
В) Если уравнение
плоскости имеет вид
![]() то она параллельна оси
то она параллельна оси
![]()
30. Выберите верное утверждение:
A)
Если уравнение плоскости имеет вид
![]() то она параллельна оси
то она параллельна оси
![]()
Б) Если уравнение
плоскости имеет вид
![]() то она проходит через ось
то она проходит через ось
![]()
В) Если уравнение
плоскости имеет вид
![]() то она параллельна оси
то она параллельна оси
![]()
31. Условие
параллельности двух плоскостей
![]() и
и
![]() имеет вид:
имеет вид:
А)
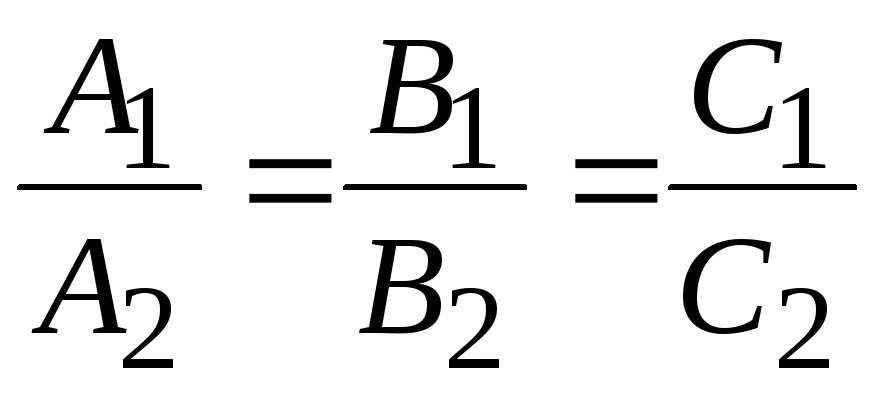 ;
;
Б)
![]() ;
;
В)
![]() .
.
32. Условие
перпендикулярности двух плоскостей
![]() и
и
![]() имеет вид:
имеет вид:
А)
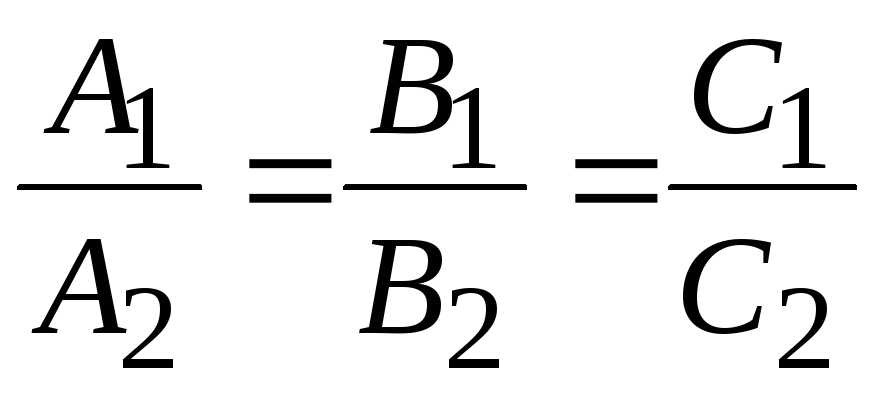 ;
;
Б)
![]() ;
;
В)
![]() .
.
33. Условие
перпендикулярности прямой
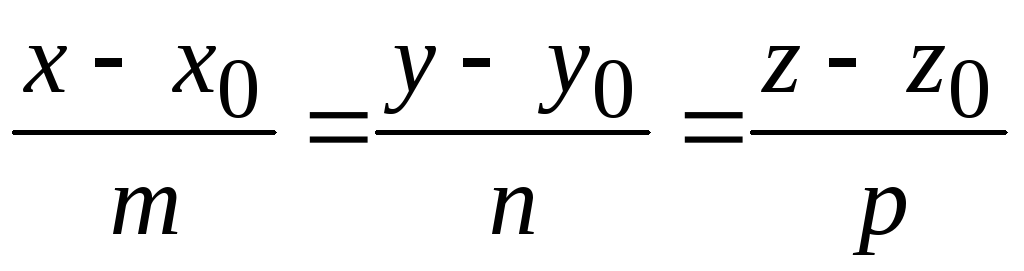 и плоскости
и плоскости
![]() имеет вид:
имеет вид:
А)
![]()
Б)
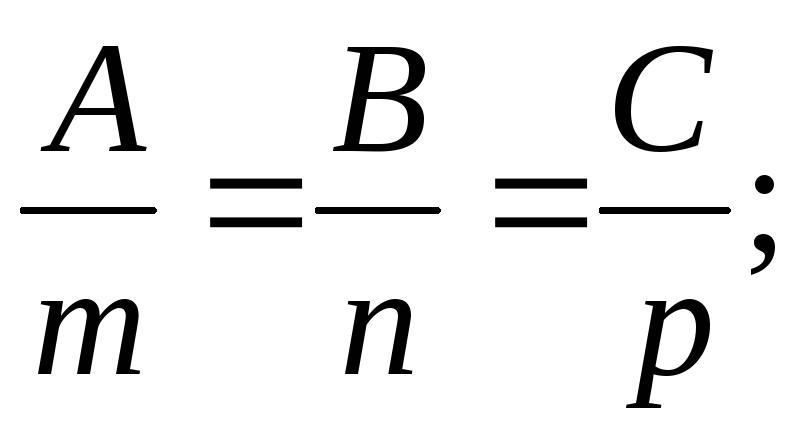
В)
![]()
34. Условие
параллельности прямой
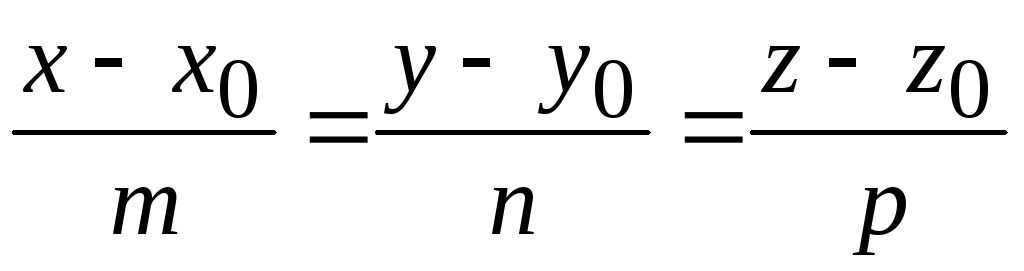 и плоскости
и плоскости
![]() имеет вид:
имеет вид:
А)
![]()
Б)
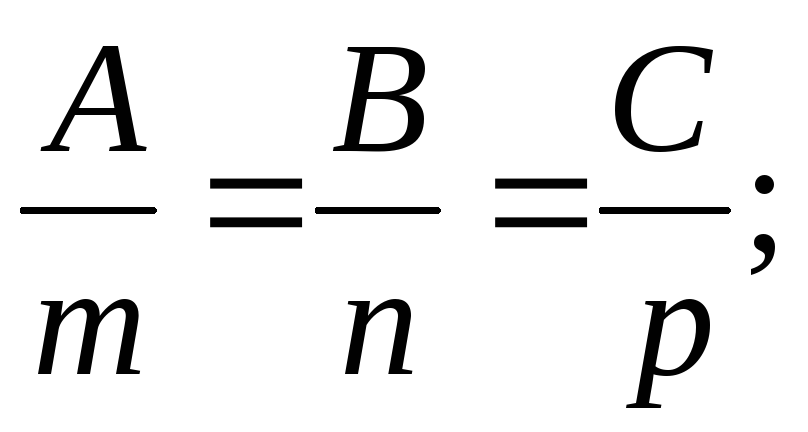
В)
![]()
35. Условие
параллельности прямых
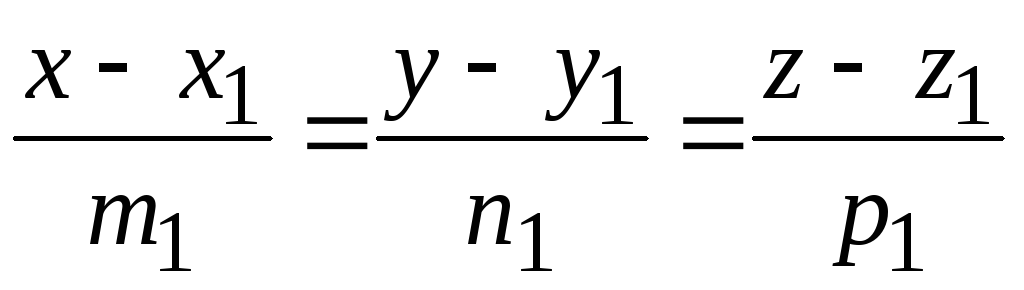 и
и
 имеет вид:
имеет вид:
А)
![]()
Б)
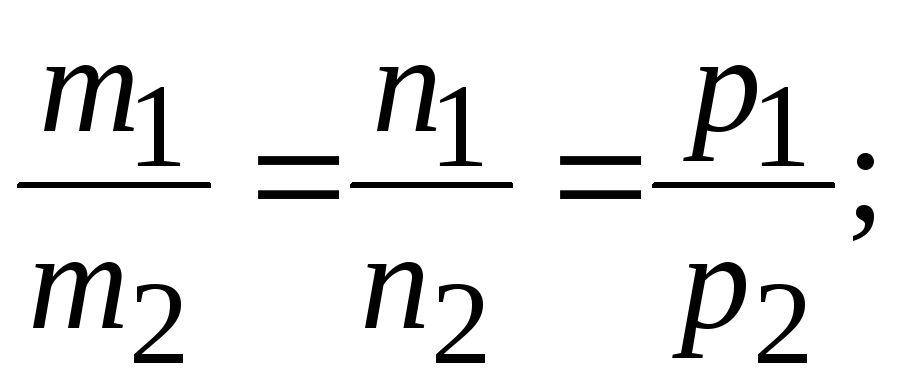
В)
![]()
36. Условие
перпендикулярности прямых
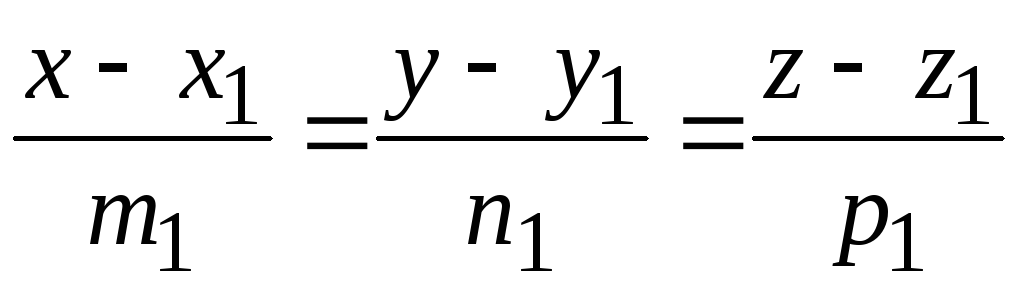 и
и
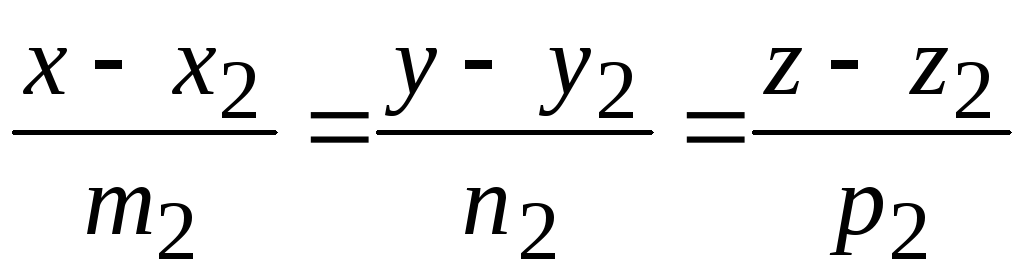 имеет вид:
имеет вид:
А)
![]()
Б)
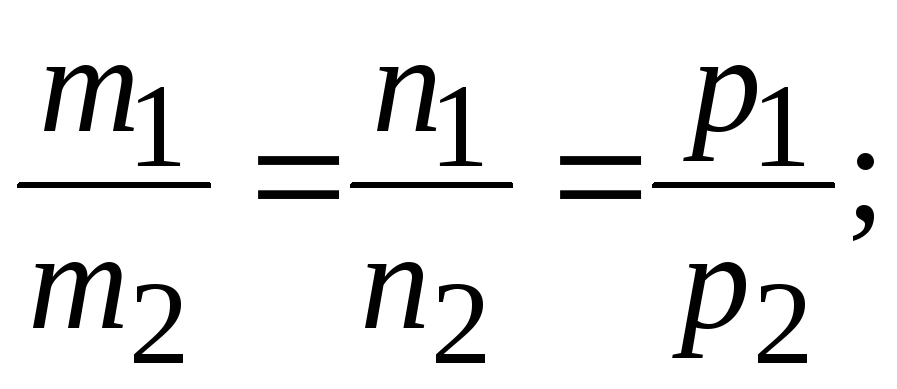
В)
![]()
37. По какой формуле
вычисляется длина вектора
![]() :
:
А)![]()
Б)
![]() ;
;
В)
![]() ;
;
Г).![]() ;
;
38. Чему равны
направляющие косинусы вектора
![]() (6;
2; 3):
(6;
2; 3):
А)![]() ;
;
![]() ;
;
![]()
Б)![]() ;
;
![]() ;
;
![]() ;
;
В)![]() ;
;
![]() ;
;
![]() ;
;
Г)![]() ;
;
![]() ;
;
![]() .
.
39. Как вычисляется скалярное произведение двух векторов, заданных своими координатами:
А)
![]() ;
;
Б)
![]() ;
;
В)![]() ;
Г)
;
Г)![]()
40.Определитель
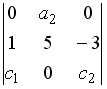 равен…
a)
равен…
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
41.
Даны матрицы
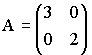 и
и
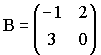 .
Тогда A∙B равно …
.
Тогда A∙B равно …
А)
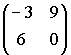 Б)
Б)
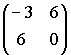
В)
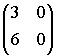 Г)
Г)
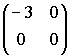
42.
Дана матрица
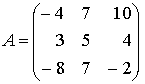 .
.
Тогда сумма элементов, расположенных на главной диагонали
этой матрицы, равна…
А)11 Б) 7 В) -1 Г) 1
43.Дана
матрица
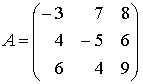 .
Тогда сумма элементов
.
Тогда сумма элементов ![]() этой
матрицы, равна…
этой
матрицы, равна…
А) 1 Б) 9 В) 19 Г)–9
44.
Определитель
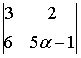 равен
0 при
равен
0 при
![]() =…
=…
А) 1 Б)–4 В) 0 Г) 2
45.
Если (x0,y0) – решение системы
линейных уравнений
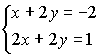 ,
тогда
x0–y0 равно…
,
тогда
x0–y0 равно…
А) –0,5 Б) 0,5 В) –5,5 Г) 5,5
46.
Если (x0,y0) – решение системы
линейных уравнений
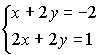 ,
тогда
x0+y0 равно…
,
тогда
x0+y0 равно…
А) –0,5 Б) 5,5 В) 0,5 Г) –5,5
47.
Векторы ![]() и
и
![]() перпендикулярны,
если k равно…
перпендикулярны,
если k равно…
А) 3 Б) 2 В)–3 Г)–2
48.
Векторы ![]() и
и
![]() коллинеарны,
если k
равно…
коллинеарны,
если k
равно…
А) –2 Б) 1 В) 2 Г) –1
49. Нормальный
вектор плоскости
![]() имеет
координаты…
имеет
координаты…
А) (1;2;1) Б) (2;1;–15) В) (1;2;–15) Г) (1;1;–15)
50. Прямая проходит через точки О(0;0) и В(–4;8). Тогда ее угловой коэффициент равен…
А) –2 Б) 4 В) 2 Г) –4
51.
Если
![]() ,
,
![]() и
и
![]() ,
тогда угол между векторами
,
тогда угол между векторами
![]() и
и
![]() равен
...
равен
...
А)
![]() Б)
Б)
![]() В)
В)
![]() Г) 0
Г) 0
52.
Если уравнение гиперболы имеет вид
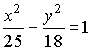 ,
то
длина ее действительной полуоси равна…
,
то
длина ее действительной полуоси равна…
А) 5 Б)9 В) 25 Г) 18
53.
Если уравнение эллипса имеет вид
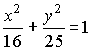 ,
то
длина его меньшей полуоси равна…
,
то
длина его меньшей полуоси равна…
А) 25 Б) 4 В) 16 Г) 5
54.
Если уравнение эллипса имеет вид
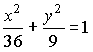 ,
то
длина его большей полуоси равна…
,
то
длина его большей полуоси равна…
А) 9 Б) 6 В) 36 Г) 3
55.
Уравнение прямой, проходящей через
точку М(1;1;–1) перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
А)
![]()
Б)![]()
В)![]()
Г)![]()
56. Расстояние между точками A(1, 2) и B(k, – 2) равно 5 при k равном …
А) – 2
Б) 10
В) 6
Г) 1
57. Как записать
через компоненты
![]()
А)
![]()
Б)
![]()
В)
![]()
Г)
![]()
58.Разложение по
первой строке определителя
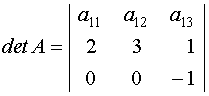 имеет
вид…
1)
имеет
вид…
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
59.Даны матрицы
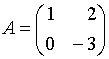 и
и
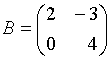 .
Тогда
.
Тогда
![]() равно
…
1)
равно
…
1)
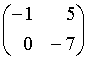 2)
2)
 3)
3)
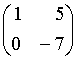 4)
4)
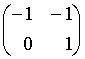
60.Матрица
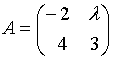 не
имеет обратной
при
не
имеет обратной
при
![]() равном…
1)
4
2)
равном…
1)
4
2)
![]() 3)
6
4)
3)
6
4)
![]()
61.Система линейных
уравнений с основной матрицей
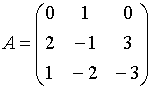 и
вектором правых частей
и
вектором правых частей 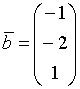 имеет
вид…
1)
имеет
вид…
1)
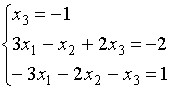 2)
2)
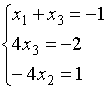 3)
3)
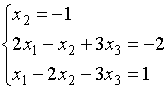 4)
4)
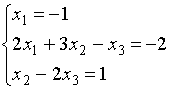
62.Ордината точки
пересечения прямой
![]() с
осью OY
равна …
1)
4
2)
- 4
3)
- 2
4)
- 3
с
осью OY
равна …
1)
4
2)
- 4
3)
- 2
4)
- 3
