23. Предел функции, свойства Раскрытие неопределённостей вида (бесконечность/бесконечность). Свойства предела функции

1.       Для того, чтобы число А было пределомf(x) приx->a, необходимо и достаточно, чтобы эта функция была представима в видеf(x)=A+альфа(х), где альфа(х) – бесконечно малая.

2.       Предел постоянной величины равен самой постоянной.LimC,x->a=C.

3.       Еслиf(x)>= 0 (f(x)<=0) в некоторой окрестности точки а, кроме самой точки а, и в этой точке имеет предел, то пределlimf(x),x->a>=0 (limf(x)x->a, <=0)

4.       Если функцииf1(x),f2(x) имеют пределы в точке а, то и их сумма, произведение и частное имеет пределы, причемlim(f1(x)+f2(x)),x->a=limf1(x),x->a+limf2(x),x->a, так же с произведением и частным

5.       Еслиf(x) имеет предел в точке а, тоlim(f(x))^n,x->a= (limf(x),x->a)^n, гдеn– натуральное число

6.       Постоянный множитель можно выносить за знак предела.Lim cf(x), x->a = cLim f(x), x->a.

7.       Если для функцийf(x),f1(x),f2(x) в некоторой окрестности в точке а выполняется неравенствоf1(x)<=f(x)<=f2(x) и пределlimf1(x),x->a=limf2(x),x->a=A, тоlimf(x),x->a=A.

8.       Limc^x,x->б = бесконечности, еслиc>1 и 0, если 0<c<1.

Неопределенность вида бесконечность на бесконечность

 

Разделить все на х в наивысшей степени, учитывая уменьшение степени в корне.

Lim(x->0) sin 5x/sin3x = [0/0]=lim(x->0) x sin5x/x sin3x = lim(x->0) sin5x/x*lim(x->0) x/sin3x=lim(x->0) 5sin5x/5x*lim 3sin3x/3x)=5/3

Lim(x-unl) (1+1/x)^x=e;

1/x=a=>x=1/a, a->0

Lim(a-0) (1+a)^1/2=e

Lim(x-0) (log_a(1+x))/x = lim(x-0) 1/x*log_a(1+x)=lim(x-0) log_a(1+x)^1/x=log_alim(x-0)(1+x)^1/x=log_ae

Lim(x-0) ln(1+x)/x=ln e=1

Lim(x-0) a^x-1/x=|a^x-1=t;a^x=t+1;ln a^x=ln(t+1)

Сравнение бесконечно малых функций

Пусть a(x,b(x) – бесконечно малые ф-ции при х->a

Тогда

1.       Lim(x->a)a(x)/b(x)=0 =>a(x) – бесконечно малая более высокого порядка, чемb(x)

2.       Lim(x->a)a(x)/b(x) =c<>0=>aиb– бесконечно малые функции одного порядка

3.       Lim(x->a)a(x)/b(x) = 1 =>aub– эквивалентные бесконечно малые функции

4.       Lim(x->a)d(x)/bⁿ(x) =c<>0 =>a– бесконечно малая функция н-ного порядка относительноb(x)

Cos2x=1-2sin²x

Теорема: если б.м. а(х) эквивалентна а₁(х) иb(x) ~b₁(x) иlim(x->a)a(x)/b(x) =>lim(x->a)a₁(x)/b₁(x)

1.       Sinkx~kx

2.       Tgkx~kx

3.       Arcsinkx~kx

4.       Arctgkx~kx

5.       E^kx-1 ~ kx

6.       A^kx~kx ln a

7.       Ln |1+kx|~kx

8.       1-cos kx ~kx²/2

23. Предел функции, теоремы о пределах. Неопределённость вида 0/0.  Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa <  имеет место неравенство f(x) > M.

lim_{x a}=

 Функция ограниченная при x a.

 Функция ограниченная при x .

 Теорема. Если lim_{x a} f(x)=b, то функция f(x) ограниченная при x a.

 Бесконечно малые и их свойства. lim_{x a} (x)=0

Теорема. 1. Если f(x)=b+, где  - б.м. при x a, то lim_{x a} f(x)=b и обратно, если lim_{x a} f(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_{x a} (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

 Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_{x a} u(x)=lim_{x a} v(x)=b, то lim_{x a} z(x)=b. ("Теорема о двух милиционерах").

 Первый замечательный предел.

0.5sin(x) < 0.5x < 0.5tg(x)

lim x 0  sin(x) x =1.

 Второй замечательный предел.

Переменная величина

  1+ 1 n   n

при nимеет предел, заключенный между 2 и 3. В данной работе мы рассмотрим неопределенность видадля функции. Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.

Пусть требуется найти предел дроби

(1)

где P(x) и Q(x) функции определенные в окрестности предельного аргумента a, но в самом предельном значении обращаются в ноль.

Теорема 1. Пусть число a для многочлена n-й степени P(x) = P_n(x) является k кратным решением, а для многочлена m-й степени Q(x) = Q_n(x) является r кратным решением, тогда

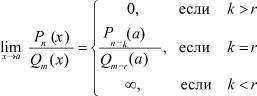(2)

где P_n-k(a) и Q_m-r(a) значения соответствующих многочленов P_n-k(x) и Q_m-r(x) в точке x = a.

Доказательство. Так как, число a является решением многочленов P_n(x) и Q_m(x), то их в любое время можно представить в виде:

Тогда

(3)

Биномы (x - a)^kи (x - a)^rв окрестности точки x = a бесконечно малы, а их основания эквивалентные бесконечно малые. Отсюда

Полагаясь на последнее равенство, можно из (3) предела получить формулу (2). 25. 1-ый Замечательный предел.

 Первый замечательный предел: