[Править]Факториальная система счисления

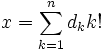В факториальной системе счисления основаниями являются последовательность факториалов , и каждое натуральное число представляется в виде:

, где .

Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: число, на единицу меньшее номера (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i! будет обозначать число инверсий для элемента i+1 в том множестве, в котором производятся перестановки (число элементов меньших i+1, но стоящих правее его в искомой перестановке)

Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём 101-ую перестановку: 100 = 4!*4 + 3!*0 + 2!*2 + 1!*0 = 96 + 4; положим ti — коэффициент при числе i!, тогда t4 = 4, t3 = 0, t2 = 2, t1 = 0 , тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, 101-я перестановка будет иметь вид: (5,3,1,2,4) Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.

[Править]Фибоначчиева система счисления

Основная статья: Фибоначчиева система счисления

Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число в ней представляется в виде:

, где  — числа Фибоначчи, , при этом в коэффициентах есть конечное количество единиц и не встречаются две единицы подряд.

[Править]Непозиционные системы счисления

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

[Править]Биномиальная система счисления

Представление, использующее биномиальные коэффициенты

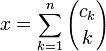, где .

[Править]Система остаточных классов (сок)

Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей с произведением так, что каждому целому числу из отрезка ставится в соответствие набор вычетов , где

…

При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка .

В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в .

Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям .

[Править]Система счисления Штерна–Броко

Система счисления Штерна–Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна–Броко.

[Править]Системы счисления разных народов [править]Единичная система счисления

По-видимому, хронологически первая система счисления каждого народа, овладевшего счётом. Натуральное число изображается путём повторения одного и того же знака (чёрточки или точки). Например, чтобы изобразить число 26, нужно провести 26 чёрточек (или сделать 26 засечек на кости, камне и т.д.). Впоследствии, ради удобства восприятия больших чисел, эти знаки группируются по три или по пять. Затем равнообъёмные группы знаков начинают заменяться каким-либо новым знаком - так возникают прообразы будущих цифр.