1.2 Методические указания по расчету цепи с нагрузкой,
соединенной треугольником
При такой схеме соединения нагрузки:
Действующее значение фазного тока в любой фазе рассчитывается по закону Ома:
При соединении нагрузки треугольником линейные токи определяются графо-аналитически на основании векторных уравнений, составленных по первому закону Кирхгофа (путем построения векторной диаграммы):
При построении векторной диаграммы необходимо определить углы сдвига по фазе между векторами фазных токов и соответствующих им напряжений:
Активная, реактивная и полная мощности определяются в той же последовательности, что и для схемы соединения «звезда».
3 Пример расчета
3.1 Расчет токов, напряжений и мощностей для схемы соединения трехфазной нагрузки звезда с нулевым проводом
Нагрузка соединена по схеме звезда с нулевым проводом представлена на рисунке 1.
Исходные данные:
1. Линейные напряжение UЛ=280 В.
2. Значения сопротивлений цепи:
Фаза А: XLA=28 Ом.
Фаза В: RB=19 Ом; XCB = 9 Ом.
Фаза С: RС=10 Ом; XLC = 20 Ом.
Определяем величину линейных токов IA, IB, Ic. Для этого рассчитаем полные сопротивления фаз приемника по формуле:
Фаза
А: 
Фаза
В: 
Фаза
С: 
Определим величину фазного напряжения:
Для заданной схемы соединения нагрузки линейные токи равны фазным:
Поэтому действующие значения линейных токов рассчитываем следующим образом:
Произведем расчет активной, реактивной и полной мощности цепи. Для этого определим коэффициенты мощности фазы приемника рассчитаем по формуле:
Фаза
А: 
Фаза
В: 
Фаза
С: 
Значение активной мощности нагрузки определяем по формуле:
Активная мощность каждой фазы:
.
Для заданной схемы:
Активная мощность нагрузки:
Значение реактивной мощности нагрузки определяем по формуле:
Реактивная мощность каждой фазы равна:
.
Для заданной схемы:
;
;
;
Реактивная мощность нагрузки:
Полная мощность нагрузки:
С помощью векторной диаграммы представленной на рисунке 3 определим ток в нулевом проводе. Ток определяем графически на основании векторного уравнения, составленного по первому закону Кирхгофа:
Рисунок 3 – векторная диаграмма токов и напряжений трехфазной нагрузки соединенной по схеме звезда с нулевым проводом
Из векторной диаграммы определяем IN:
3.2 Расчет токов, напряжений и мощностей для схемы соединения трехфазной нагрузки треугольником
Исходные данные:
1. Линейные напряжение UЛ=280 В.
2. Значения сопротивлений цепи:
Фаза
АВ: 
=28
Ом.
Фаза
ВС: RBС=38
Ом; 
=
= 27 Ом.
Фаза
СА: RСА=10
Ом; 
=
= 20 Ом.
Определим величину фазных токов IAВ, IBС, IcА. Для этого определим полные сопротивления фаз приемника:
Фаза
АВ: 
Фаза
ВС: 
Фаза
СА: 
При соединении нагрузки по схеме соединения треугольник фазные напряжения равны линейным напряжениям:
Используя полученные выше данные, получим действующие значения фазных токов приемника:
Для определения значений линейных токов построим векторную диаграмму. Рассчитаем углы сдвига между векторами фазных токов и фазных напряжений:
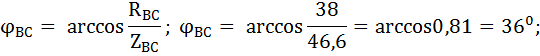
Векторная диаграмма представлена на рисунке 4. Из векторной диаграммы, на основании векторных уравнений, составленных по первому закону Кирхгофа:
определяем значения линейных токов.
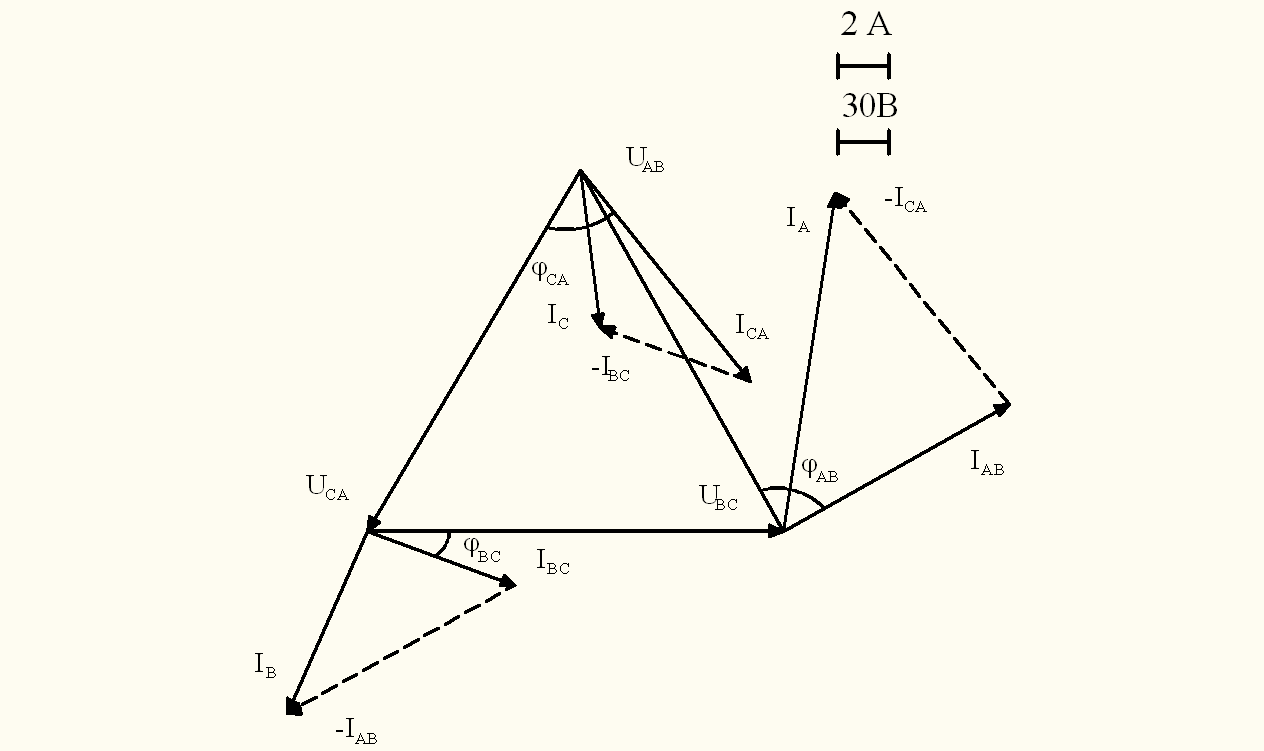
Результат:
Значение активной мощности нагрузки определяем по формуле:
Активная мощность каждой фазы равна:
Активная мощность нагрузки:
Реактивная мощность нагрузки определяется по формуле:
Реактивная мощность каждой фазы:
;
;
;
Реактивная мощность нагрузки равна:
Полная мощность нагрузки равна:
