Расчетно-графическая работа №1 расчет разветвленной цепи синусоидального тока
1 Задание для расчетно-графической работы
Разветвленная
цепь синусоидального тока (рис. 1)
находится под напряжением
,
действующее значение которогоU
= a+b,
В.
Емкостное
сопротивление
,
подключаемое с помощью выключателяS,
служит для компенсации реактивной
мощности и повышения коэффициента
мощности цепи.
Рисунок 1 – Разветвленная цепь переменного тока
Значения сопротивлений цепи принять:
,
Ом
,
Ом
,Ом
,
Ом
,
Ом
Частота: f = 50 Гц.
Значение коэффициента мощности цепи при компенсации реактивной мощности: cos φ'=0,98.
2 Методические указания по выполнению расчетно-графической работы №1
Ниже приведены методические указания по выполнению пунктов программы работы.
Действующее значение тока в любой ветви цепи рассчитывается по закону Ома:
.
Здесь
-
полное сопротивление ветви:
,
где R – активное сопротивление ветви; x – реактивное сопротивление ветви.
Угол между током каждой ветви и напряжением определяется по значению коэффициента мощности ветви:
.
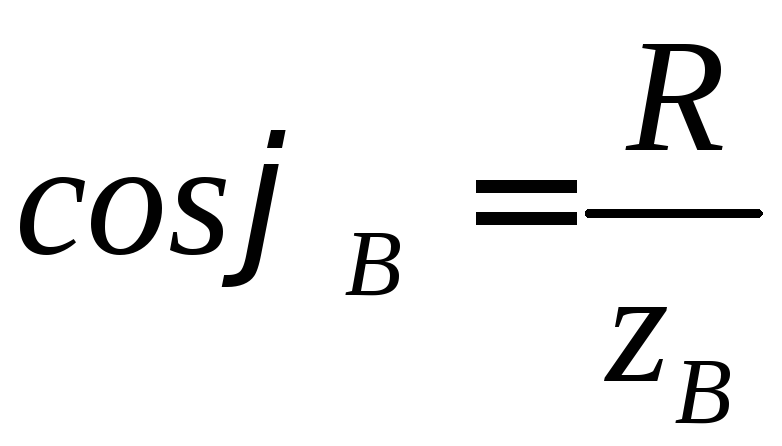При определении тока в неразветвленной части цепи графическим методом необходимо решить векторное уравнение по первому закону Кирхгофа:
.
При аналитическом методе расчета:
.
В этой формуле Y – полная проводимость цепи (См). При разомкнутом выключателе S:
,
где g – активная составляющая проводимости; b – реактивная составляющая проводимости ветвей.
Для любой ветви:
;
;
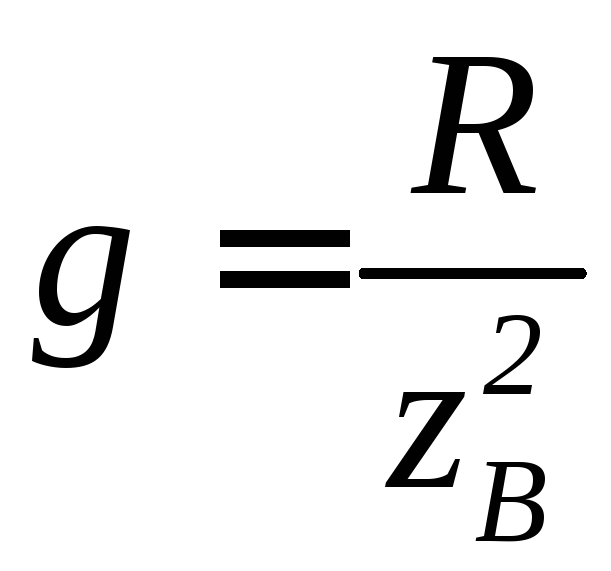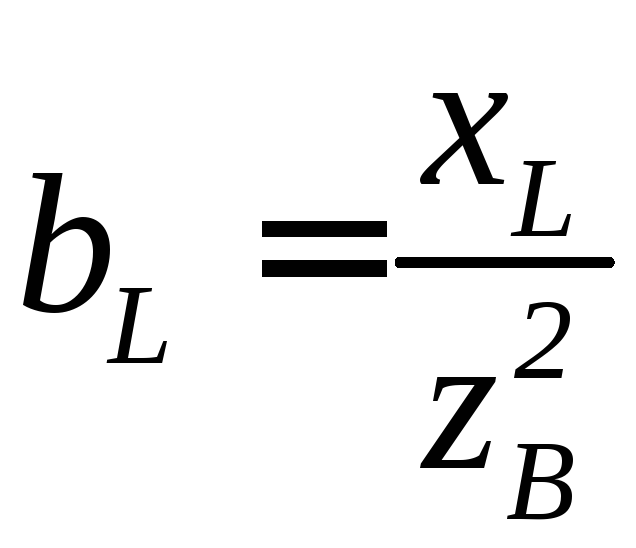Коэффициент мощности цепи:
.
Полная мощность цепи:
.
Активная мощность цепи:
.
Реактивная мощность цепи:
.
Из треугольника мощностей:
,
.
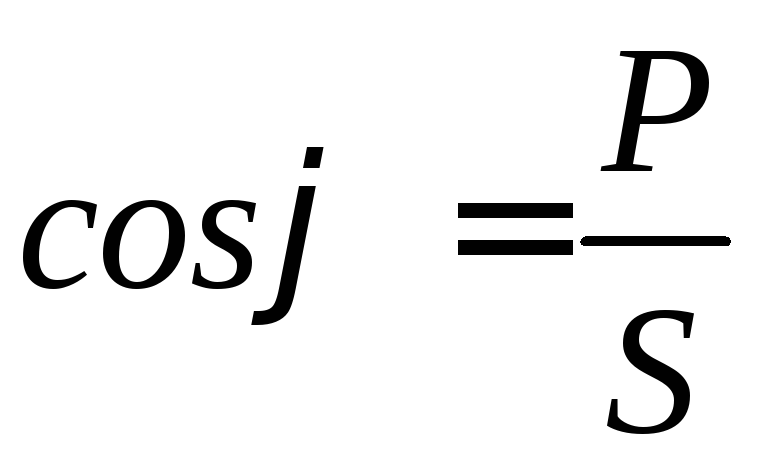Активную мощность можно определить как арифметическую сумму активных мощностей ветвей цепи. Реактивную мощность - как алгебраическую сумму реактивных мощностей ветвей (при емкостном характере сопротивления берется знак «минус»).
Для любой ветви:
;
.
Или:
;
.
Емкость конденсатора СК, подключаемого для компенсации реактивной мощности, определяется по формуле:
,
где
-угол
сдвига по фазе между токомI
в неразветвленной части цепи и напряжением
U
при разомкнутом выключателе S;
- то же при замкнутом выключателеS,
определяется по заданному значению
cos
.
Емкостное сопротивление конденсатора СК:
.
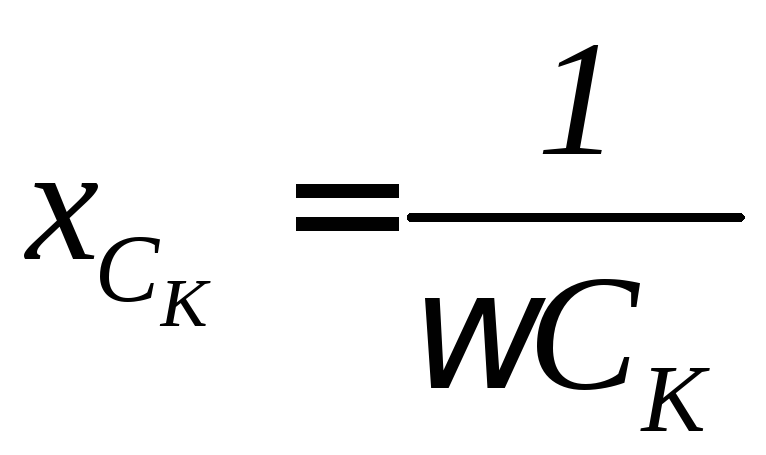При расчете тока в неразветвленной части цепи при компенсации реактивной мощности графическим методом, необходимо решить векторное уравнение:
где
-
ток, протекающий через конденсаторCК:
При аналитическом методе расчета полная проводимость цепи при компенсации реактивной мощности:
где
- реактивная проводимость ветви,
содержащей
.
Тогда значение тока в неразветвленной части цепи:
.
Полная мощность цепи:
или
.
Активная мощность цепи:
.
Реактивная мощность цепи:
.
3 Пример расчета
Исходные данные:
1. Действующее значение приложенного напряжения U=28 В.
2. Значение сопротивлений цепи:
,
Ом
,
Ом
,Ом
,
Ом
,
Ом
3. Частота f = 50 Гц.
4. Значение коэффициента мощности цепи при компенсации реактивной мощности cos φ'=0,98.
3.1 Определим токи в ветвях цепи.
Определяем полные сопротивления ветвей:
Ветвь
1: 
;
Ом.
Ветвь
2: 
,
Ом.
Ветвь
3: 
;
,
Ом.
Действующие значения токов в ветвях:
Ветвь
1: 
;
,
А.
Ветвь
2: 
;
,
А.
Ветвь
3: 
;
,
А.
Коэффициенты мощности и угол сдвига по фазе между током каждой ветви и напряжением.
Ветвь
1: 
;
;
Ветвь 2: ;
;
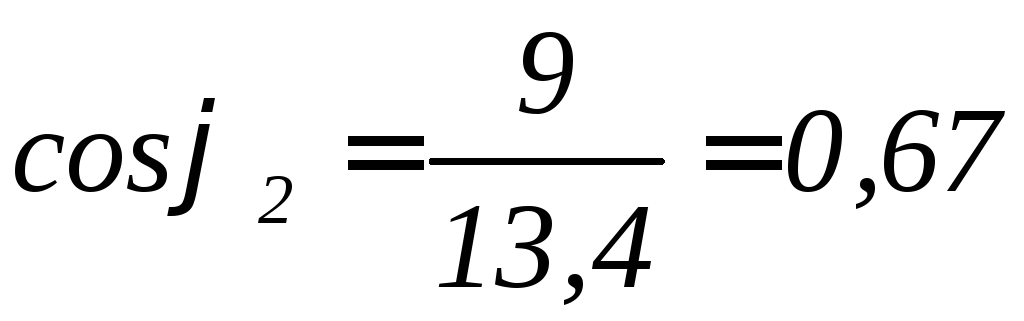Ветвь
3: 
;
;
3.2 Определим токи в неразветвленной части цепи.
Графический метод:
Ток в неразветвленной части цепи на основании первого закона Кирхгофа равен геометрической сумме токов ветвей:
С помощью векторной диаграммы (рис. 2) найдем действующее значение тока I = 3,0 A.
Рисунок 2 - Векторная диаграмма при выключенном переключателе S
Аналитический метод:
Активные составляющие проводимости ветвей:
Ветвь
1: 
;
.
Ветвь
2: 
;
См.
Ветвь
3: 
;
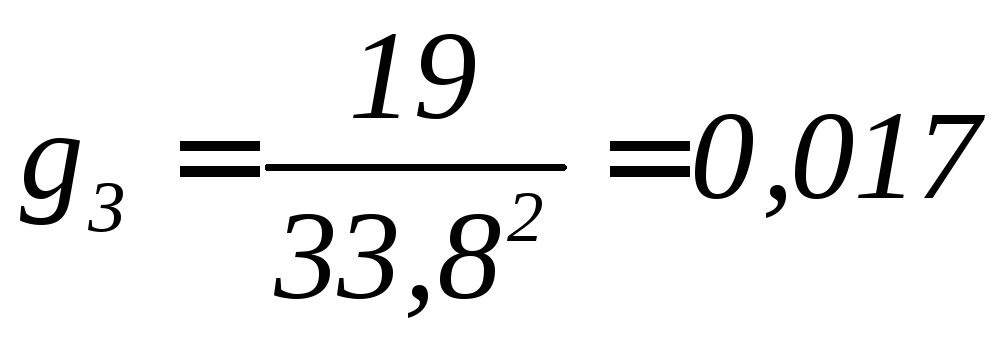См.
Реактивные составляющие проводимости ветвей:
Ветвь
1: 
;
См.
Ветвь
2: 
;
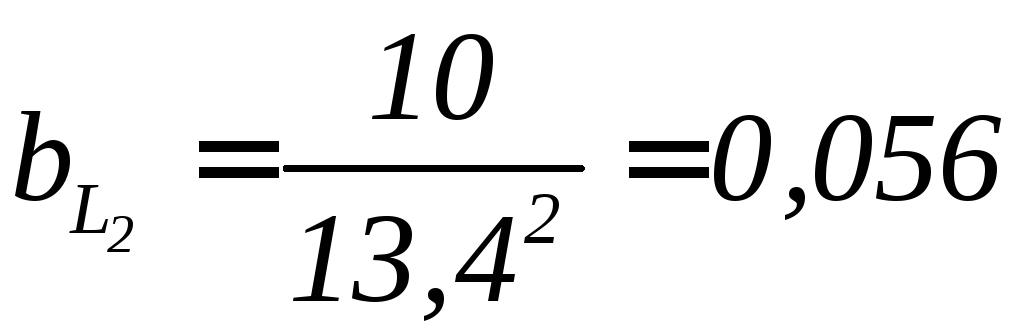См.
Ветвь
1: 
;
См.
Определим полную проводимость цепи и действующее значение тока в неразветвленной части цепи.
Полная проводимость цепи:
;
,
См.
Действующее значение тока:
;
I=28·0,108=3,03, A.
Вывод: значения тока, полученные графическим и аналитическим путем, совпадают с достаточной точностью.