7.21. .

7.27.

7.29. .

7.35.

7.45. .

7.49. .

7.57. .

7.65..

Найти производные обратных функций:

7.71. 7.72.7.75..

Найти производные от неявных функций:

7.76

7.77.

7.79 .

7.82.

7.84.

7.85 .

Найти производные функций, заданных параметрически:

7.89. 7.90.7.91..

Найти производные второго порядка функций:

7.94 7.95.7.97..

Найти производные -го порядка функций:

7.100. 7.101.7.104..

7.106. Показать, что функцияудовлетворяет уравнению.

7.107. Показать, что функцияудовлетворяет уравнению.

7.108. Показать, что функцияудовлетворяет уравнению.

7.3. Геометрические и механические приложения производной

Краткая теория

1.Геометрический смысл производной. Если кривая задана уравнениемили, тоестьугловой коэффициент касательной (тангенс угла ее наклона с положительным направлением оси абсцисс).

Уравнение касательной к кривойв точкеимеет вид:

,(7.30)

а уравнение нормали:

.(7.31)

Углом между двумя кривыми ,в точке их пересеченияназывается угол между касательными к этим кривым в точке, тангенс которого находится по формуле:

.(7.32)

2.Механический смысл производной. Если точка движения по закону, где- путь,- время, топредставляет скорость изменения пути в момент. Вторая производная пути по времениесть скорость изменения скорости или ускорение точки в момент.

7.109. Составить уравнение касательной и нормали к графику функциив точке с абсциссой.

Решение.Вычислим значение функции в точке:. Производная функции. Значение производной в точке:. Согласно (7.30), уравнение касательной имеет вид:, или, а уравнение нормали (7.31) -, или.

7.110.Составить уравнение касательной к графику функции, проходящей через точку.

Решение.Определим абсциссу точки касания из условия, что точкапринадлежит касательной, т.е. ее координаты удовлетворяют уравнению (7.30):.

Подставляя в это соотношение выражение для значения функции и ее производной в точке , получим уравнение вида:. Решая его относительно, найдем, что. Определив значение функции и ее производной в этой точке, уравнение касательной запишем в виде:, или.

7.111.Составить уравнение касательной и нормали в точке (1; 4) к кривой, заданной параметрически:,.

Решение. Найдем значение, при котором,, из решения системы:Получим, что.

Производную определим по формуле (7.27): .

Значение производной при :.

Тогда уравнение касательной запишется в виде: , или, а уравнение нормали примет вид:, или.

7.112.Найти угол между параболамиив точке их пересечения.

Решение. Решив совместно систему уравнений парабол, находим точку их пересечения:иПродифференцировав уравнения парабол,, найдем их угловые коэффициенты в точке пересечения:Согласно (7.32), тангенс угла между параболами будет равен:Следовательно,

Составить уравнение касательной и нормали к кривым в указанных точках:

7.113.

7.114.

7.115.

7.116.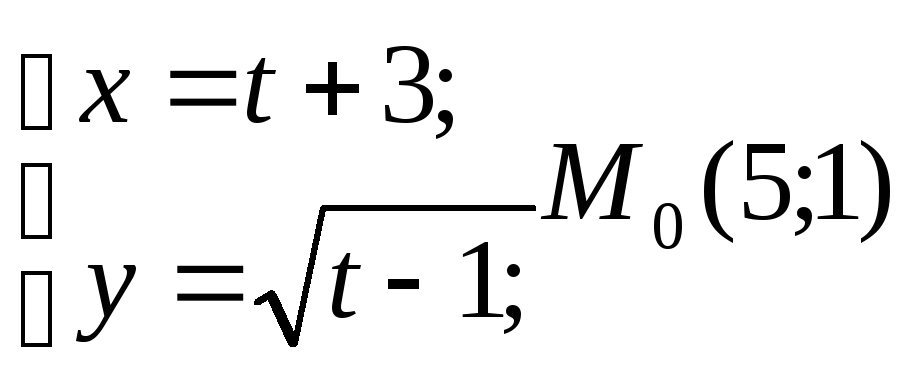

7.117.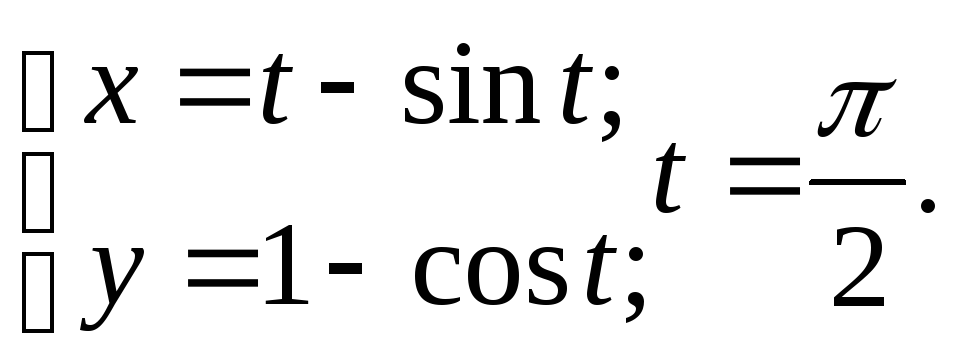

7.118.

7.119.

7.120.

7.121. Какой угол образует с осью абсцисс касательная к графику функции, проведенная в указанной точке? Написать уравнение касательной:

а)б)

7.122. Составить уравнение касательной к кривойпараллельной прямой, проходящей через точки (1;7) и (-2;2).

7.123. Составить уравнения касательных к кривойперпендикулярных прямой

7.124. Составить уравнение касательной к кривойперпендикулярной прямой, образующей с осью абсцисс угол.

7.125. Составить уравнения касательных к кривой

а) параллельных прямой

б) перпендикулярных прямой .

7.126. Составить уравнение касательной к кривой:

а) проходящей параллельно биссектрисе второго и четвертого координатных углов;

б) отсекающей на оси абсцисс отрезок, равный –1.

7.127. Составить уравнение касательной к графику функции, проходящей через точку М (6; 2).

7.128. Найти угол между кривыми:

а) и; б)и; в)и.

7.129.Тело движется прямолинейно по законуs(t). Определить скорость и ускорение тела в указанный момент времени:

а) ,; б),.

7.130. Тело, брошенное вертикально вверх, движется по закону:. Найти начальную скорость и ускорение тела () и максимальную высоту подъема (при которой скорость).