7.2 Правила дифференцирования. Производные элементарных функций. Краткая теория

I. Дифференцирование явных функций

Правила дифференцирования:

– постоянная,,– дифференцируемые функции:

(7.2)(7.6)

(7.3)(7.7)

(7.4),(7.8)

(7.5),(7.9)

Производная сложной функции. Если,, т.е., гдеиимеют производные, то

(7.10)

Производная обратной функции.Если– дифференцируемая и строго монотонная функция на промежутке, то функция обратная к данной, также дифференцируема и ее производная определяется соотношением:

,.(7.11)

Логарифмическая производная. Логарифмической производной функции называется производная от логарифма этой функции, т.е.

.(7.12)

Формулы дифференцирования основных элементарных функций:

(7.13) (7.20)

(7.14) (7.21)

(7.15)(7.22)

(7.16) (7.23)

(7.17)(7.24)

(7.18)(7.25)

(7.19)(7.26)

II. Дифференцирование неявных функций

Если зависимость между изадана в неявной форме уравнением, то для нахождения производной функциинеобходимо продифференцировать пообе части данного уравнения, рассматриваякак функцию от.Из полученного уравнения первой степени (относительно) находится.

III. Дифференцирование функций, заданных параметрически.

Если функция аргумента заданна параметрически уравнениямии, то

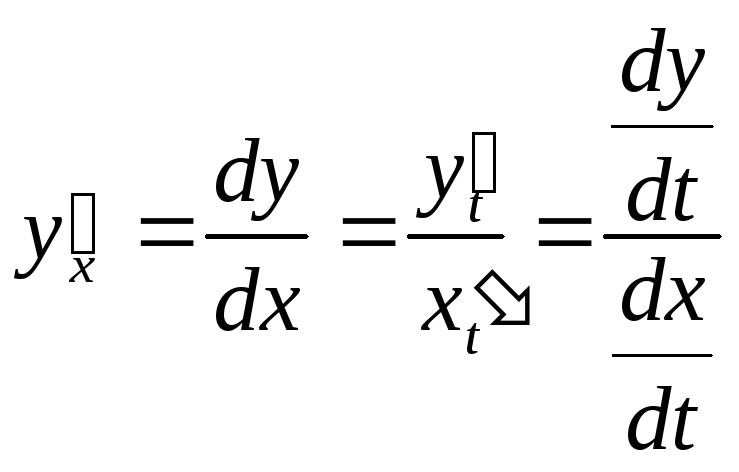.(7.27)

IV. Производные высших порядков.

Производные п-го порядканазывается производная от производной-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции:

; …;.(7.28)

Если функция задана параметрически, то

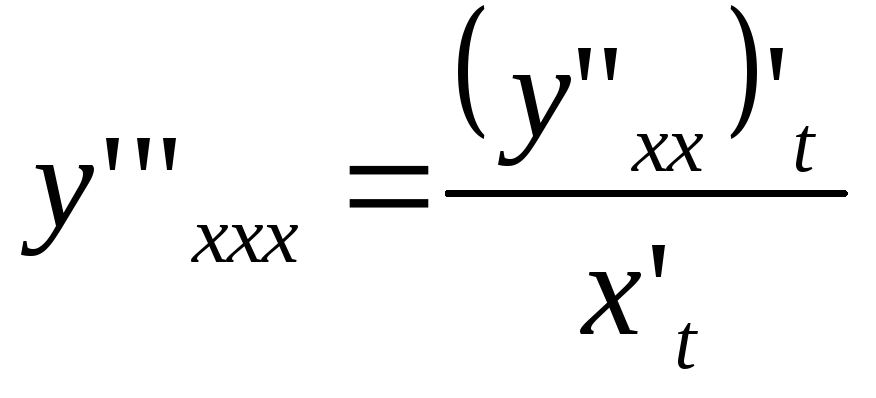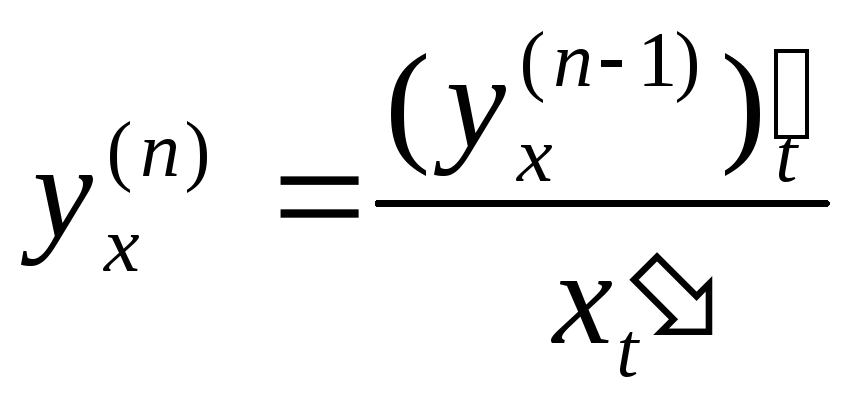;; …;.(7.29)

3. Найти производные функций:

а) ; б);

в) ; г).

Решение.

а) Используя правила дифференцирования (7.2), (7.4), (7.6) и формулы (7.13), (7.16) и (7.17) получим

.

б) Используя правила дифференцирования (7.5) и формулу (7.25), получим:

.

в) Используя правила дифференцирования (7.8) и формулы (7.19) и (7.20), получим:

.

г) Используя правила дифференцирования сложной функции (7.10) и формулы (7.13) и (7.18), получим:

.

4. Найти производнуюобратной функции, если.

Решение. Находим производную функциюпо переменной:

_.

Следовательно, согласно соотношению (7.11), получи:

.

5. Найти производные функций:

а) ; б).

Решение.

а) Имеем показательно-степенную функцию. Используя метод логарифмического дифференцирования (7.12) получим:

.

Отсюда имеем:

.

б) Здесь заданную функцию также целесообразно прологарифмировать:

.

Найдем производную:

.

Тогда, согласно формуле (7.12), получим

.

6. Найти производнуюнеявной функции.

Решение. Так какявляется функцией от, то будем рассматриватькак сложную функцию от. Продифференцировав обе части данного уравнения по, имеем

.

Разрешая последнее уравнение относительно , получим:

.

7.17.Найти производнуюфункции, заданной параметрически:

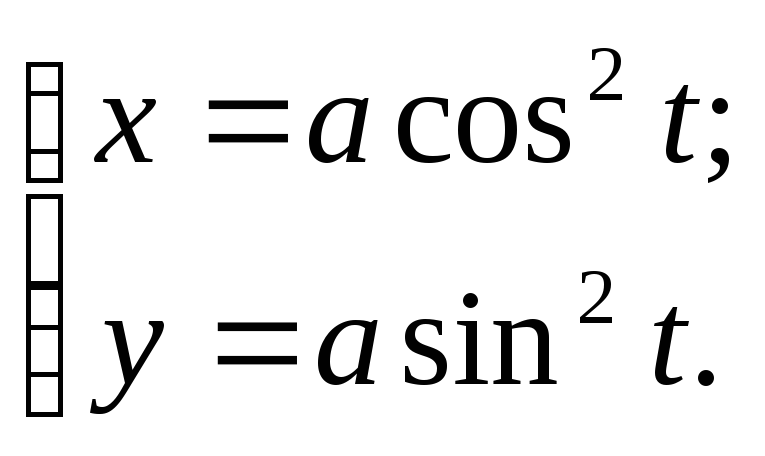
Решение.Используя правила дифференцирования функции, заданной параметрически (7.27), найдем:

и.

Отсюда .

7.18.Найти производную 4-го порядка от функции.

Решение.Последовательно дифференцируя функцию, получим:

;;;.

7.19.Найти производную второго порядка от функции, заданной параметрически:

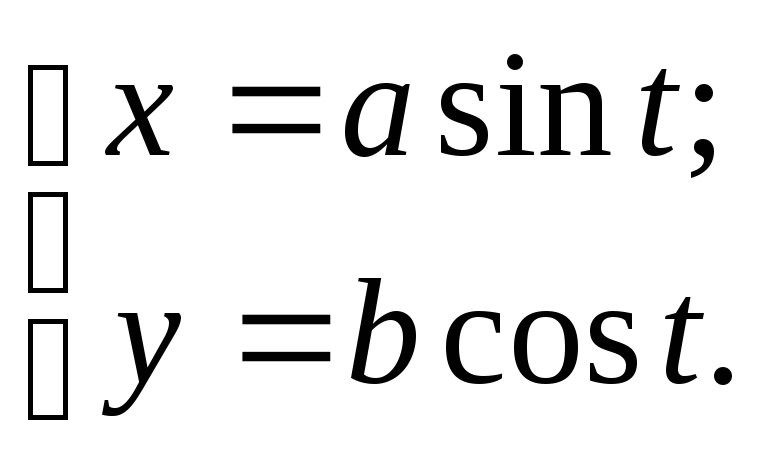
Решение. Последовательно дифференцируя функцию, получим:

;

.

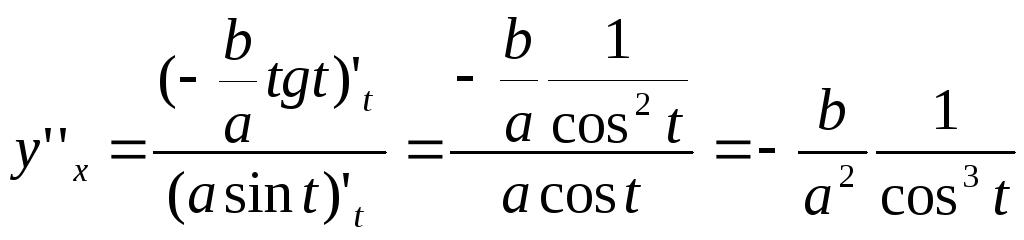7.20.Найти производнуюn-го порядка от функции.

Решение. Последовательно дифференцируя функцию, получим:

;;;

; … ;

.

Найти производные функций: