
Metodichka_lab1ab_8a
.pdf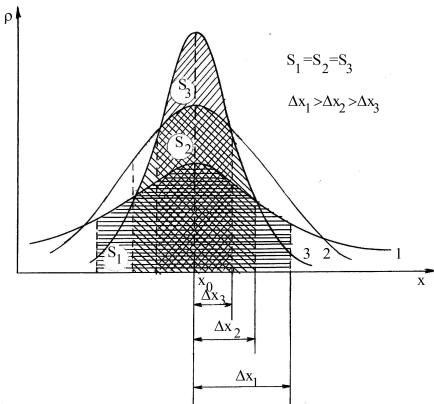
тод 1 – наименее точный, то для обеспечения условия P1 = P2 = P3 = P
(S1 = S2 = S3 ) , необходимо, чтобы интервалы x |
были связаны соотноше- |
нием x1 > x2 > x3 (рис. 3.4). Таким образом, |
величина интервала x |
связана с точностью метода: повышение точности метода приводит к уменьшению интервала x .
Рис. 3.4
При измерении произвольной физической величины х, истинное значение которой равно Аист, можно выполнить большое (в пределе – бесконечное) количество измерений. Ряд полученных результатов x1, x2 , x3, ...xn ,... называют генеральной (общей) совокупностью значений.
Разность между результатом i-го измерения (xi ) и истинным значением
(Аист) называется истинной абсолютной погрешностью i-го измерения:
ìx1 - Aист = Dx01, |
|
|||
ïx |
- A |
= Dx |
, |
|
ï 2 |
ист |
02 |
|
|
ïx3 - Aист = Dx03, |
(3.7) |
|||
í.......................... |
||||
ï |
|
|
|
|
ïx |
- A |
= Dx |
, |
|
ï n |
ист |
0n |
|
|
ï.......................... |
|
|||
î |
|
|
|
|
11
Суммирование левых и правых частей уравнений системы (3.7) даёт:
æ |
n |
ö |
= lim |
n |
limç |
åxi |
- n × Аист ÷ |
åDx0i . |
|
n→∞ è |
i=1 |
ø |
n→∞ i=1 |
|
Окончательно
|
|
n |
|
n |
|
n |
|
|
|
|
åxi |
|
åDxi |
|
åxi |
|
|
А = lim |
i=1 |
- lim |
i=1 |
» lim |
i=1 |
= x . |
(3.8) |
|
|
|
|
||||||
ист |
n→∞ |
n |
n→∞ n |
n→∞ n |
|
|||
|
|
|||||||
Следовательно, при большом количестве измерений x приближённо принимается равным Аист (однако среднее значение не равно истинному).
Математическая теория обработки результатов позволяет рассчитать
интервал é |
x - Dx |
,... |
( |
x + Dx |
ù |
, в котором с заданной вероятностью Р |
||
ë( |
сл ) |
|
сл )û |
|
xсл |
|
||
находится истинное значение измеряемой величины. Величина |
назы- |
|||||||
вается случайной составляющей погрешности. Для определения |
xсл |
необ- |
||||||
ходимо по результатам n наблюдений x1, x2 , x3, ... xn вычислить |
x и |
|||||||
приближённые абсолютные погрешности измерений xi : |
|
|
||||||
|
|
|
|
ìx1 - x = Dx1, |
|
|
||
|
|
|
|
ïx |
- x = Dx , |
|
|
|
|
|
|
|
ï |
2 |
2 |
|
|
|
|
|
|
ï |
|
|
|
(3.9) |
|
|
|
|
íx3 - x = Dx3, |
|
|||
|
|
|
|
ï.......................... |
|
|
||
|
|
|
|
ï |
|
- x = Dx . |
|
|
|
|
|
|
ïx |
|
|
||
|
|
|
|
î |
n |
n |
|
|
Для характеристики степени рассеяния результатов измерений величины xi около истинного значения Аист используется понятие дисперсии
(от латинского dispersio – рассеяние). Дисперсия обозначается символом D(x) и рассчитывается по формуле:
|
n |
|
|
|
D(x) = σ x2 = lim |
å(xi - x)2 |
|
|
|
i=1 |
|
. |
(3.10) |
|
|
n |
|||
n→∞ |
|
|
||
Здесь σ x – средняя квадратичная ошибка генеральной совокупности,
число измерений при этом бесконечно. Оценка (3.10) подобрана так, что при проведении многочисленных наблюдений погрешность в 2/3 случаев оказывается меньше σ x , а в 1/3 случаев больше, чем σ x .
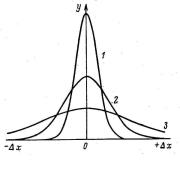
Исследуя случайные погрешности, К. Гаусс установил закон распределения случайных погрешностей, или просто закон распределения Гаусса. Согласно этому закону, при числе
Рис. 3.5
12

наблюдений, стремящемся к бесконечности, частота появления случайных погрешностей у определяется формулой:
y = |
|
1 |
|
×e- |
(Dx)2 |
|
|
|
|
2×σ 2 , |
(3.11) |
||||
|
|
|
|
||||
σ × |
|
2 ×π |
|||||
|
|
|
|
|
|
||
где σ – средняя квадратичная погрешность, x – ошибка измерения. График закона нормального распределения ошибок (3.11) представлен на рис. 3.5 для различных значений σ (σ3 > σ2 > σ1 ). Закон распределения
Гаусса отражает следующие положения теории случайных погрешностей:
1)случайные погрешности обоих знаков встречаются одинаково часто;
2)меньшие случайные погрешности встречаются чаще, чем большие;
3)очень большие погрешности маловероятны.
Закон распределения Гаусса является типичным статистическим законом. Он подергался многократным экспериментальным проверкам, которые показали, что этот закон выполняется тем точнее, чем больше проведено наблюдений. Закон Гаусса имеет основополагающее значение для разработки критериев оценок точности измерений, а также при обработке результатов физических измерений.
В реальных условиях число выполняемых измерений физической величины, как правило, невелико. Поэтому вместо генеральной совокупности значений физической величины, для которой n → ∞ , ограничиваются конечным числом n измерений. В этом случае дисперсия генеральной совокупности заменяется выборочной дисперсией:
|
|
n |
|
|
|
|
D(x) = Sx2 = |
å(xi - x)2 |
. |
(3.12) |
|||
|
i=1 |
|
||||
|
n -1 |
|||||
|
|
|
|
|
||
Среднее квадратичное отклонение отдельного измерения: |
|
|||||
|
|
n |
|
|
|
|
Sx = |
|
å(xi - x)2 |
|
|
(3.13) |
|
|
i=1 |
|
|
|||
|
n -1 |
|
|
|||
|
|
|
|
|
||
называют также средней квадратичной погрешностью измерения. Она яв-
ляется мерой разброса результатов измерений и характеризует точность применяемого метода измерений.
Среднее квадратичное отклонение результата серии измерений:
|
|
|
n |
|
|
|
Sx = |
Sx |
= |
å(xi - x)2 |
(3.14) |
||
i=1 |
|
|
||||
n |
n × |
( |
n -1 |
|||
|
|
|
|
) |
|
|
позволяет определить погрешность измерения физической величины в результате всех n выполненных измерений.
Появление конкретных случайных ошибок не является абсолютно предсказуемым событием. Об этом можно судить лишь с определённой
13

степенью вероятности. Вероятность того, что истинное значение величины
х заключено в интервале от x − |
x до x + |
x , равна: |
|
|
|
|
|
||||||||||
|
ë( |
x - Dx |
) |
< x < |
( |
x + Dx |
)û |
= α . |
|
|
|
(3.15) |
|||||
|
P é |
|
|
ù |
|
|
|
||||||||||
Здесь |
x + x называется верхней доверительной границей, |
x − |
x – ниж- |
||||||||||||||
|
|
|
|
|
|
|
ë( |
x - Dx |
) |
, |
( |
x |
+ Dx |
)û |
– доверитель- |
||
ней доверительной границей, интервал é |
|
|
ù |
||||||||||||||
ным |
интервалом. Вероятность |
α |
называется доверительной |
вероятно- |
|||||||||||||
стью и выражается в процентах или в долях единицы. Между средней квадратичной погрешностью Sx и доверительной вероятностью существу-
ет следующая зависимость: Sx соответствует α = 0,68, 2 Sx соответствует α = 0,95, 3 Sx соответствует α = 0,997. При окончательной оценке результата измерений наряду со средней квадратичной ошибкой Sx указывают
величину доверительной вероятности α . Чем выше доверительная вероятность, тем шире доверительный интервал и тем большее число измерений укладывается в этот интервал. Поэтому доверительную вероятность называют коэффициентом надёжности. При переходе к большим значениям α и сохранении прежней величины доверительного интервала необходимо уменьшить среднюю квадратичную погрешность, то есть повысить точность измерений. Точность измерений можно повысить путём увеличения числа измерений или использованием более совершенных приборов.
Поскольку при малом количестве измерений использование распределения Гаусса становится неправомерным, для оценки величины довери-
тельного интервала вводят поправочный коэффициент Стьюдента tα ,n .
Случайную погрешность измерений при малом числе наблюдений n с учётом коэффициента Стьюдента рассчитывают по формуле:
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
å(xi - x)2 |
|
|
Dx |
= t |
× S |
x |
= t |
× |
i=1 |
. |
(3.16) |
|
||||||||
сл |
α ,n |
|
α ,n |
|
n × (n -1) |
|
|
|
|
|
|
|
|
|
|
|
Коэффициент Стьюдента является функцией доверительной вероятности α и числа измерений n (приложение, табл. 1). Увеличение числа измерений или уменьшение доверительной вероятности приводят к уменьшению коэффициента Стьюдента. При исследованиях в учебной лаборатории принято использовать значения коэффициента tα ,n , равные 0,90 или 0,95.
4. Случайная погрешность прямых неравноточных измерений
Полученные выше соотношения применимы в случае, когда одинаково доверяют результату каждого отдельного измерения. Однако не всегда удаётся обеспечить полную воспроизводимость условий повторных измерений. Нередко сопоставление результатов нескольких серий наблюдений показывают, что результаты одной серии (обозначим её А) менее
14

однородны, чем в другой серии (Б). Результаты серии А заслуживают меньшего доверия, но их не следует отбрасывать. Их можно учесть, уменьшив их роль (вес) в совокупности всех результатов измерений.
Существуют и другие причины, вызывающие необходимость уменьшить роль, то есть «вес» результатов тех или иных измерений. Например, измерения могут быть выполнены различными приборами, которые дают неравноценные по точности результаты, или измерения могут проводиться различными операторами, имеющими различную квалификацию и опыт.
Чтобы выполнить основное требование теории погрешностей: обеспечить единство условий измерений в отношении всех влияющих факторов, необходимо оценить степень доверия, то есть определить «вес» всех результатов, подлежащих обработке.
Понятие «вес» отражает степень доверия к результату измерения: чем больше доверие к результату, тем больше «вес», то есть тем больше выражающее его число. В этом случае значение измеряемой величины, наиболее близкое к её истинному значению, определяется по формуле:
x = |
x1 × p1 + x2 × p2 + x3 × p3 + ... + xn × pn |
, |
(4.1) |
||
|
|||||
0 |
p1 |
+ p2 |
+ p3 + ... + pn |
|
|
|
|
||||
где x1, x2 , x3,...xn – средние значения для отдельных групп измерений, p1, p2 , p3,...pn – их «вес». Значение x0 называется средним взвешенным.
В основу вычисления «весов» взяты средние квадратичные отклонения. Веса отдельных измерений считают обратно пропорциональными
квадратам средних квадратичных отклонений (Sx2 ), то есть дисперсиям:
p : p : p :...: p |
= |
1 |
: |
1 |
: |
1 |
:...: |
1 |
, |
(4.2) |
||
S2 |
S2 |
S2 |
S2 |
|||||||||
1 2 3 |
m |
|
|
|
|
|
|
|||||
|
|
|
1 |
|
2 |
|
3 |
|
m |
|
|
|
где дисперсию j-й серии измерений определяют по формуле (3.13):
|
n |
|
|
Sxj = |
å(xi − x)2 |
|
|
i=1 |
. |
||
n −1 |
|||
|
|
Предположим, например, что тремя наблюдателями проведены три группы измерений. В результате определены средние значения, а по формуле (3.13) определены дисперсии каждой серии:
1)x1 = 395,45; Sx1 = ±0,05;
2)x2 = 395,15; Sx1 = ±0,20;
3)x3 = 395,60; Sx1 = ±0,10.
Определим отношение весов: |
|
|
|
|
|
|
|
|
|
|||||
p : p |
|
: p = |
1 |
: |
1 |
: |
1 |
= |
1 |
: |
1 |
: |
1 |
= |
|
(0,05)2 |
(0,20)2 |
(0,10)2 |
0,025 |
0,04 |
0,01 |
||||||||
1 |
2 |
3 |
|
|
|
|
|
|
||||||
= 400: 25:100 =16:1: 4.
15
В |
соответствии с полученной пропорцией определяем веса: |
||
p1 =16; |
p2 =1; p1 = 4. |
|
|
Тогда среднее взвешенное значение равно: |
|
||
|
x = 395 + 0,45×16 + 0,15×1+ 0,60 × 4 |
= 395,46. |
|
|
0 |
16 +1+ 4 |
|
|
|
|
|
Существуют и другие критерии для определения весов. Если число наблюдений в каждой серии опытов различно, а дисперсии одинаковы, то в качестве критерия для определения весов используют число наблюдений. В этом случае веса определяют по формуле:
|
p1 : p2 : p3 :...: pm = n1 : n2 : n3 :...: nm. |
|
|
|
(4.3) |
|||||||
С учётом соотношения (4.3) формула (4.1) принимает вид: |
||||||||||||
|
|
x = |
x1 × n1 + x2 × n2 + x3 × n3 + ... + xm × nm |
, |
(4.4) |
|||||||
|
|
|
|
|
||||||||
|
0 |
|
|
n1 + n2 + n3 |
+ ... + nm |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
где n1 + n2 + n3 + ... + nm = n – общее число измерений во всех группах: |
||||||||||||
|
|
n1 |
|
|
n2 |
n3 |
|
nm |
|
|||
|
|
åxi |
|
|
åxi |
åxi |
|
åxi |
|
|||
x = |
i=1 |
; x = |
i=1 |
; x = |
i=1 |
; ...x |
= |
i=1 |
, |
|||
|
|
|
|
|||||||||
1 |
|
n1 |
2 |
3 |
|
m |
|
nm |
|
|||
|
|
|
|
n2 |
n3 |
|
|
|||||
|
n1+n2 |
+n3 +...+nm |
причём |
x1 × n1 + x2 × n2 + x3 × n3 + ... + xm × nm = |
å |
|
|
i=1 |
n
xi = åxi .
i=1
Таким образом, формула (4.4) преобразуется к виду:
|
n |
|
|
|
åxi |
|
|
x = |
i=1 |
= x. |
(4.5) |
|
|||
0 |
n |
|
|
|
|
|
Например, предположим, что были проведены три группы измерений с различным числом наблюдений, а значения дисперсии во всех сериях измерений оказались приблизительно одинаковы. Результаты трёх серий измерений:
1)x1 = 25,4925; n1 = 36;
2)x2 = 25,4920; n1 = 24;
3)x3 = 25,4919; n1 = 60.
На основании пропорции (4.3) можно записать:
p1 : p2 : p3 = 36: 24:60 = 3: 2:5.
Следовательно, веса серий измерений равны: p1 = 3; p2 = 2; p3 = 5.
Среднее взвешенное значение равно:
x0 = 25,49 + 0,0025×3 + 0,0020 × 2 + 0,0019 ×5 = 25,4921. 3 + 2 + 5
5. Учёт инструментальной погрешности
Погрешности измерительных приборов определяются их классом точности, который обычно выражается в процентах. Класс точности изме-
16
рительного прибора можно принять приближённо равным максимально возможной приведённой погрешности, определяемой формулой:
δ = х / хN , |
(5.1) |
где xN – нормированное значение величины, например, |
xN = xMAX , где |
xMAX – максимальное значение измеряемой величины. Амперметр класса
точности 0,2 позволяет производить измерения с абсолютной погрешностью, не превышающей 0,2 % от тока, соответствующего полной шкале прибора.
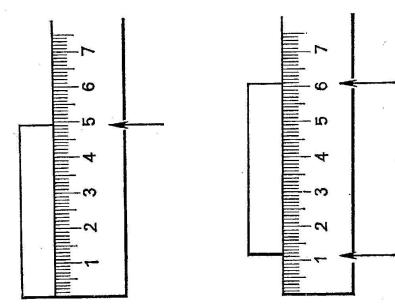
Способ измерения линейных размеров, при котором располагают линейку так, чтобы один её край совпал с одним концом предмета, и отсчитывать показания у другого конца (рис. 5.1а) годится только для грубых измерений. Для получения более точных результатов предмет следует располагать таким образом (рис. 5.1б), чтобы можно было снимать показания у обоих концов. Это связано с тем, что край линейки может оказаться испорченным, или нулевая отметка поставлена неверно. Погрешность измерений, производимых с помощью линеек, принимается равной половине цены деления шкалы.
а |
б |
|
Рис. 5.1 |
Если случайная погрешность значительно меньше инструментальной погрешности ( xСЛ = xПР ), то общая погрешность результата равна по-
грешности измерительного прибора ( х ≈ хПР ). В этом случае повторные
измерения не сопровождаются разбросом и достаточно ограничиться дву- мя-тремя повторными измерениями для исключения грубой погрешности. Такое соотношение погрешностей указывает на необходимость повышения чувствительности измерительного прибора.
17
Если случайная погрешность существенно превосходит инструментальную (DxСЛ ? DxПР ), можно попытаться увеличением числа измерений
уменьшить случайную погрешность до значений, сопоставимых с инструментальной погрешностью. Однако расчёты показывают, что это требует увеличения количества измерений до значений, практически нереальных. Такая ситуация может быть обусловлена несовершенством метода, свойствами объекта исследования или использованием прибора с необоснованно высокой точностью. В последнем случае достаточно заменить измерительный прибор, чтобы обеспечить равенство случайной и инструментальной ошибки.
Полагая случайную и инструментальную составляющие погрешности взаимно независимыми, суммарную погрешность можно определить их геометрическим суммированием:
Dx = Dx |
2 + Dx |
2 . |
(5.2) |
СЛ |
|
ПР |
|
При этом суммарной погрешности приписывается та же доверительная ве-
роятность α , как и при вычислении случайной погрешности. |
|
||||
Результат измерений следует представить в виде: |
|
||||
x = x ± |
x , |
(5.3) |
|||
указав доверительную вероятность (α ). |
|
|
|
|
|
Эта запись должна быть дополнена информацией об относительной |
|||||
погрешности: |
x |
|
|
|
|
E = |
|
× |
100 % . |
(5.4) |
|
|
|
||||
|
|
x |
|
|
|
6.Случайные погрешности косвенных измерений
Втех случаях, когда физическая величина не может быть определена непосредственно, для её нахождения используют косвенные измерения.
При косвенных измерениях значение физической величины находят на основании известной зависимости y = f (x1, x2 , x3, ... xn ) этой величины у от
величин x1, x2 , x3, ... xn , определяемых из прямых измерений.
Для независимых аргументов xi средняя абсолютная погрешность y определяется с помощью правил дифференцирования, причём символ
дифференциала d заменяют символом |
, обозначающим ошибку, то есть: |
||||||||||||||||
|
æ |
¶f |
ö2 |
2 |
æ |
¶f |
ö2 |
2 |
æ |
¶f ö2 |
2 |
æ |
¶f ö2 |
2 |
|
||
Dy = |
ç |
|
÷ ×(Dx1 ) |
|
+ ç |
|
÷ ×(Dx2 ) |
|
+ ç |
|
÷ ×(Dx3 ) |
|
+ ...ç |
|
÷ ×(Dxn ) |
|
,(6.1) |
¶x1 |
|
¶x2 |
|
|
|
|
|
||||||||||
|
è |
ø |
|
è |
ø |
|
è |
¶x3 ø |
|
è |
¶xn ø |
|
|
||||
где ∂f / ∂xi – частная производная функции f по xi в точке измерений x1 ; x1, x2 , x3, ... xn – абсолютные погрешности определения величин
x1, x2 , x3, ... xn .
Пример 1. Если функция представляет собой сумму или разность величин x1 и x2 , определяемых из прямых измерений ( y = x1 ± x2 ), то под-
18
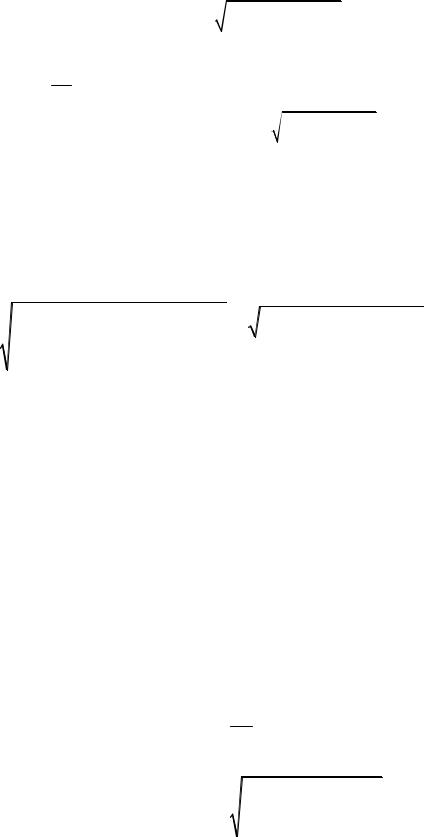
становка частных производных |
∂f |
=1, |
∂f |
= ±1 в формулу (6.1) позволяет |
|
¶x |
¶x |
||||
|
|
|
|||
|
1 |
|
2 |
|
выразить абсолютную погрешность косвенного измерения:
Dy = 
 (Dx1 )2 + (Dx2 )2 .
(Dx1 )2 + (Dx2 )2 .
Пример 2. Функция имеет вид: y = sin x . Определяем частную про-
изводную: ¶¶yx = cos x , подстановка которой в формулу (6.1) позволяет вы-
разить абсолютную погрешность: Dy = 
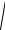 (cos x × Dx)2 = cos x × Dx.
(cos x × Dx)2 = cos x × Dx.
|
Пример |
3. |
|
Функция |
имеет |
вид: |
y = |
x1 |
|
|
. Дифференцирование |
|||||||||||||||||
|
|
x - x |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(x1 - x2 ) - x1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||
функции даёт: |
|
|
|
|
¶y |
= |
-x |
; |
|
|
¶y |
(x1 |
-x |
|||||||||||||||
|
|
|
|
¶x1 = |
(x1 - x2 )2 |
(x1 - x2 )2 |
|
|
¶x2 = |
- x2 )2 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
Подстановка полученных соотношений в формулу (6.1) позволяет |
|||||||||||||||||||||||||||
выразить абсолютную погрешность: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
ö2 æ |
|
ö2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Dy = |
æ |
x ×Dx |
x × Dx |
|
|
|
(x2 ×Dx1 )2 + (x1 |
× Dx2 )2 |
. |
|
|
|||||||||||||||||
ç |
2 |
1 |
|
÷ |
+ ç |
1 |
2 |
÷ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(x1 - x2 )2 |
(x1 - x2 )2 |
|
|
|
|
(x1 - x2 )2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
èç |
ø÷ |
èç |
ø÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если величина у определяется с помощью формулы, удобной для логарифмирования, то проще найти относительную погрешность, а затем
рассчитать её абсолютное значение. |
|
|
|
Относительная погрешность определяется по формуле (5.3): |
|
||
Ey = |
y |
× 100 % . |
(6.2) |
|
|||
|
y |
|
|
Поскольку дифференциал натурального логарифма равен: |
|
||
d (ln y) = dyy , |
|
||
то, заменяя символ дифференциала символом |
и у символом y , получим: |
||
D(ln y ) = |
Dy |
|
|
|
. |
(6.3) |
|
y |
|||
Подстановка выражения (6.3) в формулу (6.2) позволяет определить относительную погрешность косвенного измерения:
Ey = Dyy = D(ln y),
окончательно
|
y |
|
|
é |
¶ |
( |
ln f |
) |
ù |
2 |
|
|
D |
|
n |
|
|
|
|||||
Ey = |
y |
= |
åê |
|
|
|
× Dxi ú |
. |
(6.4) |
||
|
¶x |
|
|||||||||
|
|
|
i=1 |
ë |
|
|
i |
|
û |
|
|
19

Пример 1. Функция имеет вид: а) y = x1 × x2 или б) y = x1 . x2
1). Логарифмируя функции y , получим:
а) ln y = ln x1 + ln x2 ; б) ln y = ln x1 − ln x2 . 2). Определяем частные производные:
а) |
¶(ln y) |
= |
1 |
; |
¶(ln y) |
= |
1 |
; б) |
¶(ln y) |
= |
1 |
; |
¶(ln y) |
= - |
1 |
. |
(6.5) |
¶x |
x |
¶x |
x |
¶x |
x |
¶x |
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
||||||||
|
1 |
|
1 |
|
2 |
|
2 |
|
1 |
|
1 |
|
2 |
|
2 |
|
|
Здесь под величинами x1 и x2 понимаются их средние значения.
3). Подстановка частных производных (6.5) в формулу (6.4) позволяет выразить относительную погрешность:
Ey = |
æ |
|
ö2 |
æ |
|
ö2 |
|
|
|
|
|
||||||
ç Dx1 |
÷ |
+ ç Dx2 |
÷ |
= Ex21 + Ex22 |
||||
|
è |
x1 |
ø |
è |
x2 |
ø |
|
|
Пример 2. Функция имеет вид y = a × x , где а –
тель.
1). Логарифмируем функцию у: ln y = ln a + ln x .
2). Определяем частную производную: |
|
¶ln y |
= |
1 . |
||||||
|
|
¶x |
||||||||
|
|
|
|
|
|
|
x |
|||
3). Подстановка частной производной |
¶ln y |
|
|
|
||||||
|
|
¶x |
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
æ |
Dx ö2 |
|
|
|
|
|
|
||
Ey = |
|
|
2 |
= Ex . |
||||||
ç |
÷ = |
|
Ex |
|||||||
|
è |
x ø |
|
|
|
|
|
|
|
|
Пример 3. y = a × xb . 1). ln y = ln a + b ×ln x .
2). ¶¶lnxy = bx .
|
|
|
æ b |
|
|
|
ö2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3). Ey = |
× Dx |
|
b |
2 |
|
|
2 |
|
= b × Ex . |
|
|
|
|
|
||||||||||
ç |
|
÷ = |
|
|
× Ex |
|
|
|
|
|
|
|||||||||||||
|
|
|
è x |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. |
y = |
a × x1 × x2 |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
π ×(x |
|
- x ) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
||
1). ln y = ln a + ln x1 + ln x2 - lnπ - ln(x3 - x4 ). |
||||||||||||||||||||||||
|
¶ln y |
1 |
|
¶ln y |
1 |
|
|
|
|
|
¶ln y |
1 |
|
|||||||||||
2). |
¶x1 |
= |
|
|
; |
¶x2 |
= |
|
; |
|
|
|
|
= |
|
|
. |
|||||||
x1 |
|
x2 |
|
¶(x3 - x4 ) |
x3 - x4 |
|||||||||||||||||||
|
|
|
æ |
|
|
|
ö2 |
æ |
|
|
|
ö2 |
|
æ |
|
|
|
ö2 |
|
|
||||
3). Ey = |
|
ç Dx1 |
÷ |
+ ç Dx1 |
÷ |
|
+ ç |
Dx3 + Dx4 |
÷ . |
|||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
è x1 ø |
è x1 ø |
|
|
è |
|
x3 - x4 ø |
|||||||||||||||
.
постоянный множи-
20
