КМ - Maple

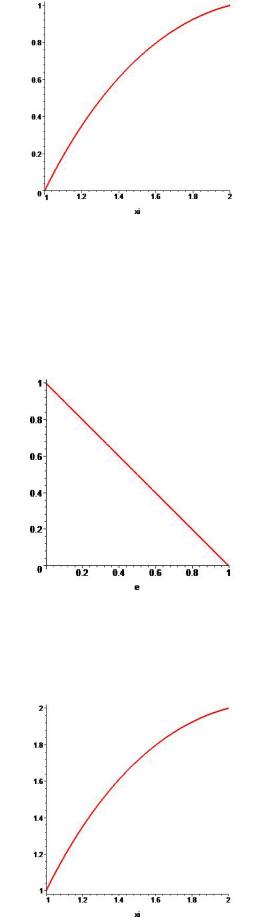
2. Внешний цилиндр неподвижен:

Функция p(e) линейно убывает на отрезке [0,1], принимая на его концах значения, равные соответственно 1 и 0. Функция является монотонно убывающей с постоянным углом наклона, равным −1.

>p := e -> 1-e; plot(p(e), e=0..1);

>b := 6; a := 3;

>V := xi -> -1/4*xi^2+(b+5*a)

/(4*a*ln(b/a))*ln(xi)+5/4; plot(V(xi), xi=1..b/a);

121

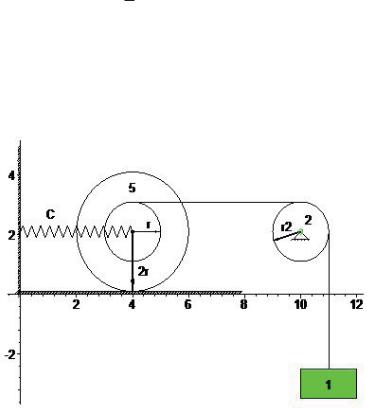
Пример № 3

√

Заданы условия x = r 2, m1 = 1, m2 = 2, m5 = 4, c = 40, t0 = 0, y0 = 0.1, v0 = 7. Определить частоту и период малых, свободных колебаний механической системы с одной степенью свободы, пренебрегая силами сопротивления и массами нитей. Найти уравнение движения груза 1, приняв за начало отсчета положение покоя груза 1 (при статической деформации пружины). Найти также амплитуду колебаний груза 1.

Воспользуемся уравнением Лагранжа 2-го рода для консервативной системы. Приняв за обобщенную координату системы вертикальное отклонение y груза 1 от положения покоя соответствующей статической деформации пружины, имеем:

> Diff(Diff(T,Diff(y,t)),t)-Diff(T,y)=-Diff(P,y);

где Т — кинетическая энергия системы, а Р — потенциальная энергия системы. Кинетическую энергию Т вычислим с точностью до величины 2-го порядка малости относительно обобщенной координаты y .

Найдем кинетическую энергию системы равную сумме кинетических энергий тел 1, 2, 5. Поскольку нить, соединяющая тела 1 и 5, невесома, нерастяжима и не проскальзывает, а тело 5 также движется без скольжения, то, как видно из рисунка:

>restart;

v1 = Diff(y,t); omega2 = v1/r; omega5 = v1/(3*r); v5 = 2*v1/3;

>T1 := (m1*v1^2)/2;

T2 := (m2*v1^2)/4;

T5 := (m5*v1^2/3); T := T1+T2+T5;

122

Потенциальная энергия определяется работой силы тяжести и работой силы упругости пружины.

>g := 9.81: y := ’y’: P1 := -m1*g*y;

P2 := c*(f[ст]+lambda[k])^2/2-c*f[ст]^2/2; P := P1+P2;

>lambda[k] := 2*y/3:

m1 := 1: m2 := 2: m5 := 4: c := 40: sas := {diff(P, y), y=0};

>solve(sas);

>f[ст] = -.367875: diff(T, v1);

>T := 14/3*Diff(y, t):

>k := sqrt((4*c)/(9*m1+9*m2/2+6*m5)); Diff(y,t$2)+(k^2)*y=0;

y0 := 0.1; v0 := 7;

>k := 4/21*sqrt(105):

y := C1*cos(k*t)+C2*sin(k*t);

>C1 := y0: C2 := v0/k: y := y;

>a := sqrt(C1^2+C2^2): b := arctan(C1/C2): sol := 3.587826640*sin(4/21*10.25*t+0.028);

>plot(sol, t=-5..5, title="Решение");

>with(plots):

with(plottools):

>pruzh := proc(x1,x2,y,r,K) local d,l:

l := (x2-x1): d := l/K: PLOT(CURVES([[x1,y],

seq([x1+j*d,r*sin(Pi*j/2)+y],j= 0..K), [x2,y]])):

end:

123

> Колесо := proc(xk, yk, R, w::anything) ‘plottools/disk‘([xk,yk], R, color=w):

end proc:

> Опора := proc(x,y,R) local x0, x1, y0, h, N:

x0 := x-R*0.7: x1 := x+R*0.7:

y0 := y-R*0.7: h := 3*R: N := 2: display(PLOT(circle([x,y],R,color=green)),

PLOT(CURVES([[x0,y0],[x-h,y-h]], [[x1,y0],[x+h,y-h]], [[x0-h,y-h],[x1+h,y-h]], seq([[x0-h*(-j/N+1),y-h],

[x0-h*(-j/N+1)-h/4,y-h*1.3]], j=0..2*N+1)))):

end:

> Поверхность := proc(x, y, L, h) local N:N:=round(abs(L/h))-3:

display(PLOT(CURVES([[x,y],[x+L,y]],

seq([[x+L*j/N/2,y], [x+L*j/N/2-h,y-h]],

j=0..2*N)))):

end:

> Стенка := proc(x, y, L, h) local N:

N := round(abs(L/h))-3: display(PLOT(CURVES([[x,y],[x,y+L]],

seq([[x,y+L*j/N/2], [x-h,y+L*j/N/2-h]],

j=0..2*N)))):

end:

> Cir := proc(x, y, R) global CLR:

PLOT(circle([x,y], R, color=CLR)) end:

> box := proc(x, y, A, B) local X, Y:

X := x; Y := y; PLOT(POLYGONS([[X-A,Y+B],[X+A,Y+B],

[X+A,Y-B],[X-A,Y-B]], COLOR(RGB,0,1,0))):

end:

124

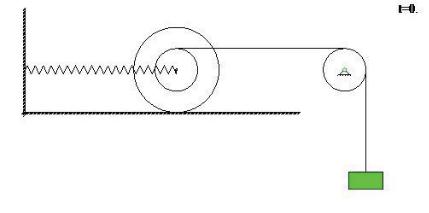
>CLR := BLACK:

>pdif := proc(eq, T)

local rec, i, dt, cadr, TT; cadr := T*50;

dt := T/cadr;

for i from 0 to cadr do

rec := box(16,-3-eval(eq,t=dt*i),.8,0.4); TT := ‘plots/textplot‘

([18,5,cat("t=",convert(evalf(dt*i,4),string))]);

q||i:=‘plots/display‘(

{rec,TT, Поверхность(-0.1,0.1,13,0.1), Cir(15,2.1,1), Опора(15,2.1,0.08), Стенка(0,0,5,0.1),

line([16,2.1],[16,-2.6-eval(eq,t=dt*i)]), Cir(7+eval(eq,t=dt*i),2.1,1), Cir(7+eval(eq,t=dt*i),2.1,2), line([7+eval(eq,t=dt*i),3.1],[15,3.1]), pruzh(0,7+eval(eq,t=dt*i),2.1,0.2,75), Колесо(7+eval(eq,t=dt*i),2.1,0.05,GREEN)}, scaling=constrained);

end do; ‘plots/display‘([seq(q||i,i=0..cadr)],

insequence=true, scaling=constrained, axes=none);

end proc:

> pdif(sol,5);

125

Пример № 4

Пренебрегая массой плиты и считая ее абсолютно жесткой, найти уравнение движения груза D массой m с момента соприкасания его с плитой, предполагая, что при дальнейшем движении груз от плиты не отделяется. Движение груза отнести к оси x, приняв за начало отсчета положение покоя этого груза (при статической деформации пружин). Плита лежит на двух параллельных пружинах, имеющих коэффициент жесткости c1 = 600 н/см и c2 = 400 н/см. Груз D ( m = 50 кг) падает без начальной скорости с высоты h = 0.1 м в точку F плиты, находящу-

a c2

юся на расстояниях a и b от осей пружин: b = c1.

Составим дифференциальное уравнение движения груза D в проекции на ось x :

>restart; with (plots):

de := m[D]*diff(x(t),t$2) = m[D]*g-F[упр]; F[упр] := (c[1]+c[2])*(f[st]+x(t));

de;

>st1 := m[D]*g-F[упр1]; F[упр1] := (c[1]+c[2])*f[st]; f[st] := solve(st1,f[st]);

>de := expand(simplify(de));

Решим дифференциальное уравнение с учетом начальных условий:

>sol := dsolve({de,x(0)=-f[st], D(x)(0)=v[0]}, x(t)); sol1 := sol;

>g := 9.81; m[D] := 50; c[1] := 600; c[2] := 400;

f[st] := (m[D]*g)/(c[1]+c[2]);

h := 0.1;

alpha := Pi/2; v[0] := 5;

>sol1 := evalf(sol1);

>v[0] := sqrt(2*g*h);

>sol := evalf(sol);

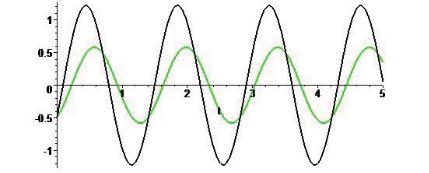
>g1 := plot({rhs(sol1)}, t=0..5,

thickness=2, color=black): > g2 := plot({rhs(sol)}, t=0..5,

thickness=2, color=green): > display(g1, g2);

126

>stenka := 0;

>plita := proc(x, alpha) ‘plottools/rotate‘(‘plottools/rectangle‘

([x,1], [x+2,5], color=green), alpha, [2,1]);

end proc:

>P := plita(6, alpha):

>z := plot(0, x=-5..7, thickness=2, color=black):

>z1 := plot(5, x=-5..7, thickness=3, color=magenta):

>strinl := proc(x,x1,alpha)

delt := abs(x-x1)/25;

points := plot([[x,0],[x,4],[x,3], seq([x+delt/2+delt*i,3+(-1)^i*0.5],

i=0..24), [x+delt*25,3]], thickness=2, color=black, scaling=constrained);

points := ‘plottools/rotate‘(points, alpha, [0,0]); end proc:

> strinp := proc(x, x1, alpha) local str, delt, points; delt := abs(x-x1)/11;

points := plot([[x,0], [x,4], [x,-5], seq([x+delt/2+delt*i,-5+(-1)^i*0.5],

i=0..10), [x+delt*11,-5]], thickness=2, color=black, scaling=constrained);

points:=‘plottools/rotate‘(points, alpha, [0,0]); end proc:

>pruzinal := strinl(0, 5, alpha):

>pruzinap := strinp(0, 5, alpha):

>display(z, z1, P, pruzinal, pruzinap, scaling=constrained);

127

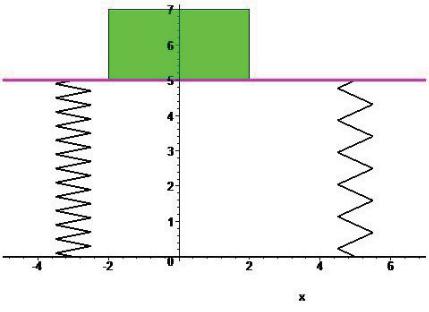
> pdif := proc(eq, alpha, T)

local r, r1, r2, p1, p2, i, dt, cadr, TT, ps, pb; cadr := T*50;

ps := ‘plottools/rotate‘ (plot([[0,-7], [0,8]],

thickness=2, color=black), alpha, [1,1]);

pb:=‘plottools/rotate‘

(plot([[5,-7]], thickness=1, color=black), alpha,[1,1]);

dt := T/cadr;

for i from 0 to cadr do

TT := ‘plots/textplot‘([7, 7,

cat("t= ", convert(evalf(dt*i,4), string))]); r := plita(6+eval(eq, t=dt*i), alpha);

r2 := plot(5+eval(eq, t=dt*i), x=-5..7, thickness=3, color=magenta);

p1 := strinl(0, eval(5+eq, t=dt*i), alpha);

p2 := strinp(0, eval(5+eq, t=dt*i), alpha); q||i := ‘plots/display‘({r,r2,pb,ps,TT,p2,p1},

scaling=constrained);

end do; ‘plots/display‘([seq(q||i,i=0..cadr)],

insequence=true, scaling=constrained, axes=NONE);

end proc:

128

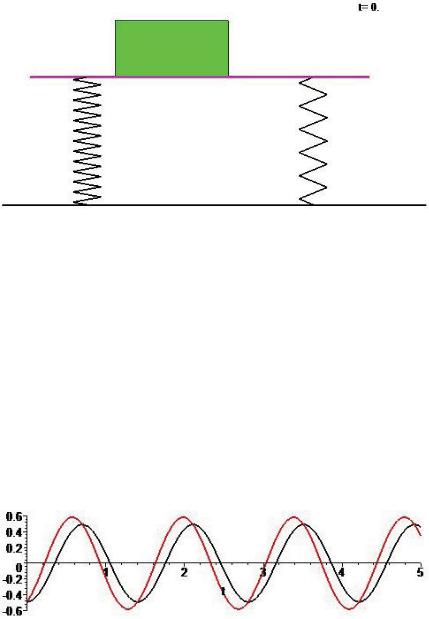
> pdif(rhs(sol), alpha, 4);

> g_1 := plot(rhs(sol), t=0..5, thickness=2, color=magenta, title="c[1]+c[2]=1000"):

>plots[display](g_1, g_2);

>plots[display](g_2);

>c[1]+c[2] := 2:

gr1 := plot(rhs(sol), t=0..5, thickness=2,

color=red, title="c=2"):

sol := dsolve({de, x(0)=-f[st], D(x)(0)=0}, x(t)); > gr2 := plot(rhs(sol), t=0..5, thickness=2,

color=black, title="c=2"): plots[display](gr1, gr2);

129

Ресурсы в Web

•http://www.maplesoft.com/ — сайт разработчика

•http://www.mapleapps.com/ — коллекция приложений

•http://www.maple4students.com/ — центр поддержки для студентов

•http://www.exponenta.ru/soft/Maple/Maple.asp — страница на популярном российском образовательном математическом портале, посвященная Maple

•http://www.dxdy.ru/ — научный форум

•http://www.studrus.ru/ — ресурс о математике и физике

130