микросхемотехника

2

УДК 621.393 С 92

Печатается по решению Научно-методического совета физического факультета

ВГУ

С 92

Схемотехника интегральных схем. Ч.1: Цифровые структуры: Методические материалы для выполнения контрольных заданий по курсу “Микросхемотехника” для студентов 5 курса д/о спец. 200.200 / Сост.: В.И.Клюкин, Е.В.Невежин; Воронеж. гос. ун- т, физ. фак., каф. физики полупроводников и микроэлектроники. - Воронеж, 1999. – 30 с.

Методическая разработка содержит теоретический и справочный материал для выполнения самостоятельных практических заданий по проектированию цифровых автоматов в элементной базе логических интегральных схем (ИС). Дано краткое изложение основ булевой алгебры и применения карт минтермов для синтеза цифровых субсистем. Приведены методические указания по выполнению контрольных заданий и оформлению отчета.

Методические материалы предназначены для практических занятий и самостоятельной работы студентов 5 курса специальности 200.200, а также могут быть использованы при выполнении курсовых и дипломных работ.

3

4.ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ АВТОМАТОВ С ОГРАНИЧЕНИЯМИ

4

ВВЕДЕНИЕ

К настоящему времени микроэлектроника занимает ключевые позиции в производстве электронных устройств, постоянно укрупняющихся и расширяющих функциональные возможности. Основную массу микроэлектронных изделий составляют интегральные схемы (ИС), разделяющиеся по характеру функционирования и способу представления информации на два основных класса - цифровые (логические) ИС и аналоговые ИС. При этом наиболее интенсивно развивается элементная база “крупноблочного” построения электронной аппаратуры - ИС субсистемы (счетчики, регистры, дешифраторы, блоки памяти, АЦП и ЦАП, микропроцессоры), удовлетворяющие следующим требованиям:

•выполнение типовых, широко используемых функций;

•наращиваемость, т.е. возможность изменения в широких пределах числа разря-

дов;

•ограниченное число внешних связей;

•логическая, электрическая и конструктивная совместимость между собой и с сопутствующими изделиями.

Около 80% выпускаемых микросхем составляют цифровые ИС, характеризующиеся высокой помехоустойчивостью и стабильностью выходных параметров. Научной и методической основой микросхемотехники цифровых структур выступает теория логического проектирования, использующая понятия и методы булевой алгебры (алгебры логики), вкратце (в рамках необходимого для дальнейшей работы) изложенные в следующем разделе.

5

1. ОСНОВЫ БУЛЕВОЙ АЛГЕБРЫ

Состояние входов и выходов логических элементов (ЛЭ) могут принимать только два различных значения, характеризующих не столько количественную, сколько качественную сторону происходящих изменений. Переменные, описывающие эти состояния, также принимают 2 значения (в цифровой технике “0” и “1”), причем любое изменение состояния ЛЭ соответствует переходу “0”→ ”1” или “1”→ ”0”. Возможную двойственность устраняют понятия положительной (позитивной) и отрицательной (негативной) логик, а именно: в положительной логике более высокому потенциалу соответствует логическая “1”, в отрицательной - логический “0”. Математика двузначных чисел есть алгебра логики, доказательная база (постулаты 1÷5 и основные теоремы 6÷14) которой представлена в табл. 1.1.

Приведенные в табл. 1.1 соотношения имеют двойственный характер, т.е. могут быть получены одно из другого взаимной заменой “0”↔ ”1”, (+)↔ (•). Отметим также, что в булевой алгебре справедливы переместительный и сочетательный законы.

1.1. Логические функции В булевой алгебре как аргументы, так и функции могут принимать только 2 значе-

ния, т.е. область определения булевых функций всегда конечна. Совокупность значений аргументов Z связана с числом переменных n соотношением Z =2n, а число соответствующих булевых функций, обозначающих логические операции над n переменными, равно Nz = 2z. Логические функции одной и двух переменных вместе с графическими обозначениями базисных ЛЭ приведены в табл. 1.2.

Из приведенных логических операций (функций) основной базис составляют конъюнкция и, дизъюнкция или и инверсия и, образующие функционально полную систему, достаточную для реализации любой произвольно заданной функции двоичного аргумента. Примеры других функционально полных наборов ЛЭ приведены в табл. 1.3.

Нетрудно заметить, что базисные логические функции и, или, и-не, или-не легко

обобщаются на случай n переменных: f1(xn) = x1•x2•...xn;; f7(xn) = x1+x2+...+xn; f8(xn) = =x1+ +x2+...+xn; f14(xn) = x1•x2•...•xn. Соответствующие логические устройства (аппара-

турные аналоги) будут иметь n входов.

1.2.Формы представления булевых функций

Как следует из теоремы разложения (табл. 1.1, №14), любую логическую функцию n переменных можно представить в двух стандартных формах: совершенной дизъюнктивной нормальной форме (СДНФ) (1.1), представляющей сумму минтермов mi (произведений всех переменных, в которые каждая переменная в прямой или инверсной форме входит только один раз),

8

8

и совершенной конъюнктивной нормальной форме (СКНФ) (1.2), представляющей произведение макстермов Mi (сумм всех переменных, в которых каждая переменная входит только раз)

Совокупность минтермов и макстермов для трех аргументов приведена в табл. 1.4.

Очевидно, что число минтермов (макстермов) n переменных равно 2n. Свойства минтермов и макстермов определяются соотношениями (1.3) ... (1.7).

Для получения СДНФ по заданной таблице истинности необходимо сложить минтермы тех наборов аргументов, для которых значения fi булевой функции равны 1, а для получения СКНФ - перемножить макстермы наборов с fi = 0. Действительно, для значений fi из табл. 1.4

На практике удобнее пользоваться СДНФ, графически представленной коэффициентами разложения fi на специальной карте минтермов Вейча (рис. 1.1а - для двух переменных) или Карно (рис. 1.1б - для трех переменных). Графическое изображение булевой функ-

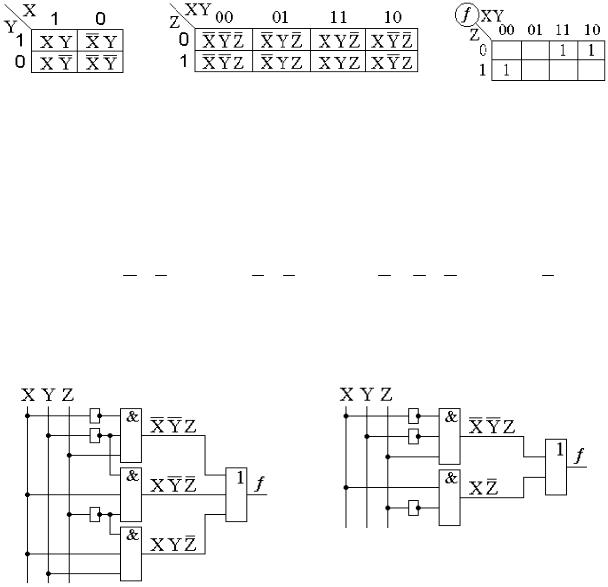
9

ции из табл. 1.4 приведено на рис. 1.1в., где пустые клетки карты минтермов Карно соответствуют fi = 0.

Рис. 1.1.

1.3.Минимизация логических выражений

Представление булевых функций в виде стандартных СДНФ или СКНФ, удобное при преобразовании логических выражений, не всегда обеспечивает оптимальную для аппаратурной реализации форму с минимальным числом букв. Легко убедиться, что СДНФ булевой функции (1.8) допускает дальнейшее упрощение

f = X • Y • Z + X • Y • Z + X • Y • Z = X • Y • Z + X • Z ,

(9 букв) (5 букв)

в результате которого при реализации требуется меньше базисных ЛЭ (6 вместо 7) и межсоединений (10 вместо 14) (рис. 1.2 а,б).

а) б)

Рис. 1.2.

Наиболее удобен метод упрощения, основанный на “склеивании” (объединении) минтермов СДНФ булевой функции, графически представленной в виде карты Вейча или Карно (типа рис. 1.1в). Правила “склеивания” минтермов (для карты Карно) следующие:

1) Допускают объединение 2m минтермов, расположенных в соседних строках (столбцах) карты минтермов;

2)соседними строками (столбцами) считаются такие, при переходах между которыми изменяет свое значение только одна переменная;

3)полученное в результате объединения минтермов выражение содержит на m букв меньше, чем любой из исходных минтермов;

4)в конечном выражении пропадают те переменные, которые при переходах между объединяемыми минтермами изменяют свое значение;