
Metodichka_-_Terver
.pdf3. Усло ны роятности |
|
|
|
|
|
||||||
íîì |
|
|
A при условии H (èëè при задан- |
||||||||
любогоОпределениесобытия . Пусть событие H имеет вероятность P H) |
6= 0. Äëÿ |
||||||||||
|
A величина |
|
|
|
|
|
|
|
|
(2) |
|
|
|
P (A H) = |
|
P (AH) |
|
||||||
|
|
|
P (H) |
||||||||
азывается условной вероятностью| |
|
|
|||||||||
ПримерH). . (Игральный кубик.) |
|
|
|
|
|
|
|
|
|
||
события: |
|
Ω = {1, 2, 3, 4, 5, 6}. ассматриваются |
|||||||||
A = {выпадение четного числа при подбрасывании игрального кубика} = |
|||||||||||
{2, 4, 6}. |
не более трех очков} = {1, 2, 3}. |
|
|
|
|||||||
H1 = { |
|
|
|
||||||||
H2 = {выпадение более трех очков} = {4, 5, 6}. |
|
||||||||||
AH1 = {2}; AH2 = {4, 6}; |
|
|
|
|
|
|
|
|
|
||
|
1 |
|
1 |
|
2 |
|
|
||||
НезависимыеP (A)ñîá= 2 |
; P (A|H1) = 3 ; |
P (A|H2) = 3 . |
|
||||||||
|
û ия. События |
|
|
|
|
|
|
|
|||
ми, если условная верояòность |
|
|
AсобытияH называются независимы- |
||||||||
зависит от |
H, ò. . |
P (A|H) |
|
A относительно H не |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
первоенаТояорусловнуюТеоремалениямыдвухсловероятностьобсобытийумножениинияравнадругого,Póìí(Aâåð|H) = P (A). |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
÷òî |
|
|
произведениювычисленнуюятностейния .вероятностиВероятностьроятностпредположении,одногосовместногой з них |
|||||||||
событие уже наступило: |
|
|
|
|
|
|
|
|
|
||
В частности дляP (независимыхAB) = P (B) ·событийP (A|B) = P (A) · P (B|A). |
(3) |
||||||||||
сляютехпроизведениюостальных,предполож. Вероятностьпричвероятностинии,мвероятностьсовместногочтоодноговсе предыдущиекаждогопоявленияиз них последующегонанесколькихсобытияусловныеужевероятнособытиянастуй |
|||||||||||
вычстиравнаСледствие |
P (AB) = P (B) · P (A). |
|
|||||||||
ïèëè: |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
- |
P (A1A2 · ... · An) = P (A1) · P (A2|A1)11· P (A3|A1A2) · ... · P (An|A1 · ... · An−1).

Теорема сложения вероятностей |
|
. Âåðî |
суммеят остьверпîÿвлениятностейхотяэтихсобытийодногобезизвероятностидвухсовместныхсобытийих совместногоравнапояв- |
||
ления: |
H1, H2, ..., Hn |
|
гипотезщих пол ауюсоответствующуюгруппу,равнасуммеусловную(ãèï |
|
|
ФормулВероятностьполнойсобытияP (A + Bроятности) = P (A) + P B) − P (AB). |
(4) |
|
нии одного из несовместныхA, котороесобытийможет |
тез)аступить лишь при появле |
|
|
|
- |
произведенийвероятностьвероятностейсобытия каждойобразуюиз |
||
(гипотез) |
A: |
|
|
|
|
n |
|
|
X |
|
|
ФормулПусть собыБ ией с P (A) = P A|Hi)P (Hi). |
(5) |
|
i=1
из несовмесòíûõA событийможетнаступить лишь при усл вии п явления однополную группу событий. Если событие H1, H2, ..., Hn, ê òòîрые образуют
гипотез могут быть переоценены |
|
ормуламA уже произошлБайеса î, |
|
роятности |
|||||||||
|
|
|
|
|
|
P (Hk)P (A Hk) |
|
|
|
|
|
||
îлстейПримерв шине.)рыВелогонщик.Вероятность1с. (рВелогонщикш теряетниямипрсобытие.коланадеждуТеоремыв шиненасложусправнаåхнияв0гонке,.и01умножения. Найтесли сделавероятностьпро(6) |
|||||||||||||
кнПрим |
P (Hk |
A) = |
|
n |
|
| |
. |
|
|
|
- |
||
|
|
|
| |
|
Pi=1 P (A|Hi)P (Hi) |
|
|
|
|
||||
ò ãî, ÷òî |
сойдет |
дистанции. |
|
|
|
дистанции}, |
|||||||
ешение. Обозначимколеса |
|
|
A = {гонщик сх дит |
||||||||||
òèÿ |
= { |
прокол первого |
} |
, |
A2 |
= { |
прокол второго колеса |
} |
. Ñîáû- |
||||
A1 |
|
|
|
|
|
|
|
|
|||||
умножения |
|
|
|
|
|
|
|
|
|
|
|||
|
A1 |
|
A2вероятностей,являютнезависимымиполучаем. Используя теоремы сложения и |
||||||||||
|
|
|
P (A) = P (A1 + A2) = P (A1) + A(A2) − P (A1A2) = |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
номПримерпорядке расставлено2. (Задача о15книгахучебников,.) На причемстеллажепятьбиблиотекиизних в переплетев случай-. |
|||||||||||||
|
= P (A1) + A(A2) − P (A1)P (A ) = 0.01 + 0.01 |
− 0.01 |
|
= 0.0199. |
|||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|

Библиот карь берет наудачу три учебника. Найти вероятность того, что |
|||||||||||||||||||||||
õîòÿ áû îä |
из взятых учебников окажется в переплете. |
|
|
||||||||||||||||||||
ешение. Обозначим событие A = { |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
. Хотя бы один из трех взятых |
|
|
||||||||||||||
Bместныхокажется= одинсобытучебникавпереплете,й:оказалсяеслипроизойдетвпереплете};любое из следующих трех несов- |
|||||||||||||||||||||||
Cников= дваоказался в переплетев переплете}еåòå}; |
|
|
|
|
хотя бы один из взятыхучебников |
||||||||||||||||||
D ={òðè |
|
â |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A =ÏîB теореме+ C + Dсложения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ности событий |
|
|
|
P (A) = P (B) + P (C) + P (D). Найдем вероят- |
|||||||||||||||||||
|
|
B, C, D: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
C51C102 |
45 |
|
|
|
|
|
C52C101 |
|
|
20 |
|
|
|
|
C53 |
2 |
|
|||||
ТогдаP (B) = |
|
|
= |
|
, |
P (C) = |
|
|
|
= |
|
|
, P (B |
= |
|
|
= |
|
. |
||||
|
C153 |
91 |
|
C153 |
|
91 |
C153 |
91 |
|||||||||||||||
|
|
|
|
|
|
|
45 |
|
|
20 |
|
2 |
67 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
îтриванннетахгербоòиеяза. Форму(т.ì.Каковаекверху.гербëà по.свероятностьдвухëíой вероятноститого,.Наугадчто.) Пустьпривы- |
|||||||||||||||||
всехбраннуюиз десятиПримербросанияхешениемонету3..Обозначим(монетаЗадачаоднабросаютбракPупадет(Aì)ñîáû= |
+ |
|
+ |
91 |
= . |
сторон) |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
91 |
|
|
91 |
91 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
кверху}, |
|
|
|
|
|
|
|
|
A = {монета три раза упала ге бом |
||||||||||||||
бракованная монета}{былавыбрана.Тогда стандартная монета}, |
H2 |
= |
{была выбрана |
||||||||||||||||||||
H1 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
9 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
, P (A|H2) = 1. |
|||||||
Используя оðìулу полной |
|
|
|
|
|
|
получаеì |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
P (H1) = |
10 , P (H2) = 10 |
P (A|H1) = |
23 |
= 8 |
|||||||||||||||||||
|
|
|
|
|
|
|
верояòíîñòè, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
9 |
|
|
|
1 |
|
|
17 |
|
|
|
|
|
|
|
|
Примерешениеупалакоторыйг монета;.рбом4.сИспользуем(ответствуетЗадачакверху2)браков. Найтимонетахтеусложеàннаявероятнобозначиям. монетаФопредыдуîñìóëàåíтьбракованная.ия,того,Баùчтоейесачтозидачи,.)былапредыдущейПустьивыбранамонетапроведентриза1) |
|||||||||||||||||||||||
разаопыт,тандартная |
|
P (A) = 8 · |
10 |
+ 1 · |
10 |
= |
80 . |
|
|
|
|
|
|
|
|||||||||
станддаче: Aртная= {монетамонета},три раза упа |
гербом кверху}, H1 = {была выбрана |
||||||||
òîì àйденных в предыдущей{бызадачеëà выбранавероятностей |
монета}. С уче- |
||||||||
|
|
H2 = |
|
|
|
|
|
|
|
9 |
|
1 |
|
1 |
1 |
|
|||
P (H1) = |
|
, P (H2) = |
|
, P (13A|H1) = |
|
= |
|
, P (A|H2) = 1, |
|
10 |
10 |
23 |
8 |
||||||

а также P (A) = 17/80, используя ормулу Байеса, получаем
Аналогично |
P (H1 |
A) = |
P (A|H1)P (H1) |
= |
9 |
. |
|
P (A) |
17 |
|
|||||
|
|
| |
|
|
|
||
белым |
P (H2 |
A) = |
| |
= . |
|
||
|
|
|
P (A H2)P (H2) |
|
8 |
|
шарвторойИмеютсяаннойбудет |
урны4т белыхиПримеродинаковыевыбирается.1черный,5. (Шарыурныодин.вишарВтретьейурныпервой. Найти. Формула2 белых3вероятностьбелыхполнойшарараитове.3Изчерных,ðîãîятности, чтонаугадэтотво.выб) |
|||||||
|
|
| |
P (A) |
|
17 |
|
|
вая урна},ешение. Обозначим A ={выб али белый шар}, H1 ={выбрана пер- Очевидно,H2 ÷òî={выбрана вторая уðíà}, H3 ={выбрана третья урна}.
|
P (H1) = P (H2) = P (H3) = 1/3. |
||
Используя |
ïîëíî2й вероятности, |
4 |
получаем |
|
|||
|
ормулуP (A|H1) = 5 , P (A|H2) = 5 , P (A|H3) = 1. |
||
|
1 |
2 |
1 |
4 |
1 |
11 |
|
|
îмйЗадачаполкебудет в1ра.случайСобраседьмымположениеомсочиненнапорсвоÿтретийдкем,.èйНтизàðòîìéåñåüåì,ìè1)òâомовероятпорядрасполагаетсястьêîí вом того,месте;чтона2)третийусловкниж |
||||||||
нуютЗ чи |
P (A) = 3 |
· 5 |
+ 3 · |
5 |
+ 3 |
· 1 = 15 . |
|
- |
вероя |
òîãî, ÷òî |
|
|
|
окажется на третьем месте, при |
|||
условии, чòность |
на полке стоит седьмой том. |
|
являются |
|||||
Задача 2. Известно, что 5 % всех мужчин и 0.25 % женщ |
||||||||
дальто иками. Случайно выбранное лицо оказалось дальтоником. Найти |
||||||||
вероятíость того, что это мужчина. |
|
|
|
|
|
|||
неизвестногопом щении цветаящикзатерялсяов. (Из оставшихсябелых,вероятностьящикекрас- |
||||||||
ных)Задачаодин 3шар. При |
|
|
|
N |
M |
N |
− M |
|
|
выбираютможетбелым?передаватьсяпосредственном,одиншар. Каковаодному |
èç |
òîãî, |
|||||
N÷òî−Задачавынутый1 шаров4. шарСообщениеслучайноокажется |
|
|
|
|
|
|
|
|
связи, находящихся в различных состояниях; из них |
|
n каналов |
||||||
личном состоянии, |
|
|
|
|
n1 |
каналов от- |
||
( |
n2 в хорошем, n3 |
|
|
|
n4 |
плохом |
||
n = n1 + n2 + n3 + n4). Вероятность14 правильной передачи сообщения
для разного вида каналов равна соответственно надва.трехвероятностьразакостяхпо.одномуДлявыпалитого,пои- |
|||
разные |
|
p1, p2, p3, p4 |
|
чтотомувышенияЗадачахотяжеграни?быбыканалу,его5.наодинБросаютсядостоверностиоднойкоторыйразизононихтрибудетвыбираетсявыпаласообщениеигральныепереданоединица,наугадпередаетсякостиправильесли.. КаковаНайти |
|
||
4. Случ йны личины. Ч сло ы х р к- |
|||
т ристики случ йных |
личин |
|
|
Определ ние. Под случайной велич |
ой понимается величина, ко- |
||
торая в опыт |
со случайным исходом принимает то или иное значение. |
||
осизначенияватьщая. |
ϕ |
величина, |
|
Случайная величина U есть числовая ункция элементарного события ω |
|||
Множество возможных зн ченийU = ϕ(ω). |
|
(7) |
|
значений, которые принимает ункцияU = (u1, u2, ..., un ...) состоит из всех |
||||||||
|
|
|
|
|
|
|
- |
|
НепрерывнаяДискретная.отд ленныекоторойслучайнаяслучайнаядругнепрерывноотдругавеличинавеличиназаполняютзначения,случайнаяслучайнаякакой.которые-то промежутоквеличина,можноперенумеровозможныечисловойинимаю |
||||||||
Законом распределения |
|
|
величины называется всякое соот |
|||||
ношение, устанавливающееслучайнойязь между возможными значениями слу |
||||||||
чайной величины |
соответстâующими |
вероятностями. Закон распре- |
||||||
деления может иметь разные ормы. |
|
|
|
|||||
перечисленыределения дискретнойвозможныесоответствующимислуч(различные)йной вел значенияныназываетсяэтойслу- |
||||||||
чайнойт блица,ядомвеличиныгдерас |
|
|
|
|
|
|
|
X |
|
x1, x2, ..., xn |
|
|
|
|
им вероятностями |
||
p1, p2, ..., pn: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
x1 |
x2 |
|
xn |
|
ãäå |
|
pi |
|
p1 |
p2 |
... |
pn |
|
Pn
никомpðài =распределенияPическое(x = xизображениеi), (ðèñi p.i =1).1ряда. 15распределения называется многоуголь-
=1
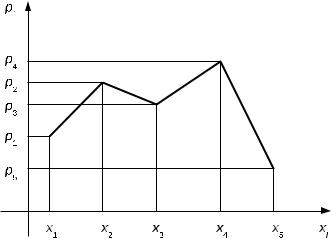
Функция р спр л ния èñ. 1 |
|
|
|
|
||||
наяПустьвеличинаx есть некоторое д йствительное |
исло. Событие, что случай- |
|||||||
|
|
|
|
|
÷ |
, обозначим как |
U < x |
. |
Вероятность этогоU приметсобытиязначåние меньшее,рассматриваемаяx |
|
|||||||
|
|
|
P (U < x) |
|
|
как ункция от |
||
x, называется ункцией распределения случайной величины U : |
|
|
||||||
СвойстваФункция ункциираспределенияраспределенияF (x) = P (U < x). |
|
(8) |
||||||
щими из определения: |
F (x) обладает двумя свойствами, следую- |
|||||||
Функция |
F (−∞) = 0, |
F (+∞) = 1. |
(9) |
|||||
|
|
F (x) есть неубывающая ункция своего аргумента: |
|
|
||||
ФункцияЗнание распределенияункции распределениявероятностипри |
ñîáû èé |
(10) |
||||||
|
|
F (x2) |
≥ F (x1), |
|
x2 |
> x1. |
|
|
|
событий, связанных |
|
|
|
ò найти вероятности |
|||
любых |
|
|
со случайF (случайнойx) величинойпозволяе |
|
|
|||
бытия |
|
|
|
|
|
U . Вероятность со |
|
|
|
|
|
заданному интерваëуичиныинтервале: езу ь |
|
||||
тате опытаB = {будетα ≤ Uпринадлежать< β}, что значение |
|
U |
|
|
||||
ется как приращение ункции распределения на этом [α, β), опредеëÿ- |
||||||||
|
|
P (α ≤ U < β)16= F (β) − F (α). |
(11) |
|||||
ассмотрим три события:
События A = {U < x1} |
B = {x1 ≤ U < x2}, |
C = {U < x2}. |
|
||||
опытаВероятностьбудетA иравнB бытия,отдельномучтозначениепризначению:этомслучайнойC = A + Bвеличины. в результате |
|||||||
несовместны, |
|
|
|
|
|
|
|
Замечание. ЕслиP Uункцияu |
lim [F (x) |
− |
F (u |
)]. |
(12) |
||
( |
= i) = x ui |
|
i |
|
|
||
|
|
→ |
|
|
|
|
|
заданного значения |
|
F (x) непрерывна, то вероятность любого |
|||||
величиныПлотностьюназываютрасроятностPïределенияервую(U = xпроизводную) =éâåð0. ятностейот ункцииепрерывнойраспределения:случайной
0
Для непрерывной случайнойf (x) = Fвеличи′(x) = |
d |
|
íûF (ормулаx). |
(11) принимает (13)вид |
|
|
dx |
|
|
|
|
|
β |
|
|
Свойства1 |
плотностиPвероятностейα ≤ U < β = |
Zα |
f (x)dx. |
(14) |
||
3. |
Z f (x)dx = 1 |
(условие нормировки). |
|
|||
2. |
f (x) |
≥ 0. |
|
|
|
|
∞
−∞
x
Z
МатематическоеЧислоF (x)û= õ fскимр(tожидание)êòdtожиданием. ристики случучайноййныхвеличиныличин
−∞
среднее значени , вычисляемое по ñë17едующим ормуламX. называется ее
1. Для дискретной случайной величины:
n
X
2. Для непрерывной случайнойM [X] =величины:xipi.
i=1
|
|
∞ |
|
|
|
МатематическоеожиданиеM [X] = Z |
xf (x)dx. |
|
|
||
|
|
−∞ |
|
|
|
Простейши.1 |
свойства мат |
M [X] |
кратко обозначается |
mX |
. |
|
|||||
неслучайнойжиданвелè÷èíû. |
|
||||
|
|
матического |
|
|
|
величине |
|
|
|
c равно самой |
|
c: |
|
|
|
|
|
2. При прибавлении к случайнойM [c] =величинеc. |
|
|
|||
|
|
|
X неслучайной величины |
||
c к ее математическому ожиданию прибавляется та же величина: |
|||||
3. При умножении случайнойM [X + c]величины= M [X] +íàc.неслучайную величину |
|||||
на ту же величину |
|
|
|
c |
|
|
c умножается ее математическое ожидание: |
||||
чайных4.Математическоевеличинравноожиданиепроизведениюжителей: M [cXпроизведения] = cMматематических[X]. взаимно ожиданнезависèймыхсомнослу--
математических5.МатематическоеMожиданий[X ожиданиеX ...Xслагаемых:] =суммыM [X ]случайныхM [X ]...M [величинX ]. равно сумме
1 2 n 1 2 n
случайнойЦентрированнойM [величинойX + X +случайной... + X ] =величинойM [X ] + Mназывается[X ] + ... +разностьM [X ]. между
1 2 n 1 2 n
X и ее математическим ожиданием:
˚ −
X = X18 M [X].
Дисперсия
даниеДисперсиейквадратаслучайнойсоответствующейвеличиныцентрированнойX называется случайнойматематическоевеличины:ожи-
˚2
Дисперс.Для1 дискретнойя вычисляетсяслучайнойпоD[Xследующим]величины:= M [X ]. ормулам.
n
X
2. Для непрерывнойD[случайнойX] = (xвеличины:i − M [X])2 pi.
i=1
|
|
|
∞ |
|
|
|
|
Дисперсия |
|
D[X] = |
Z |
(x − M [X])2 f (x)dx. |
|||
|
|
|
−∞ |
|
|
|
|
1 |
D[X] |
кратко обозначается |
DX . |
|
|||
Простейшие.Дисперсиясвойстванеслучйнойдисперсиивеличины. |
|
|
|
||||
|
|
|
|
|
c равна нулю: |
||
2. При прибавлении к случайнойD[c] =величине0. |
|
||||||
|
|
|
|
|
|
X неслучайной величины |
|
c ее дисперсия не меняется: |
|
|
|
|
|
||
3. При умноже ии случайнойD[X +величиныc] = D[X]. |
|
||||||
|
|
|
|
|
|
X на неслучайную величину |
|
c ее дисперсию умножают на c2: |
|
|
|
||||
дисперс4.Дèсперсияйслагаемых:суммы независимыхD[cX] = c2Dслучайных[X]. |
величин равна сумме |
||||||
Средним квадратическим отклонением случайной величины |
|||
D[X1 + X2... + Xn] = D[X1] + D[X2]... + D[Xn]. |
|||
зывается корень квадратный из дисперсии |
σX = √ |
|
X íà- |
|
|
. |
|
19 |
DX |
||
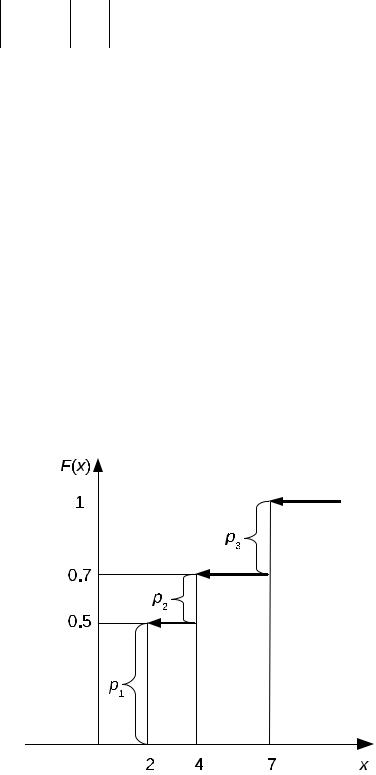
Прим ры с р ш ниями
пределенияПример 1. Дискретная случайная величина U задана законом рас-
|
|
|
U |
|
2 |
|
4 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найти ункциюp |
|
|
0распределения.50.20.3 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величинать ее гра ик. |
||
|
ешение. Значений, меньшихF (числаx) начерт2, |
|
|||||||||||||||
образом, при |
|
|
|
|
|
|
|
|
|
|
|
|
|
U не примет. Таким |
|||
|
|
|
x ≤ 2 F (x) = P (U < x) = 0. |
|
|
|
|||||||||||
|
Åñëè < x ≤ 4 |
|
F (0x.)5.= 0.5 |
|
|
|
|
U |
|||||||||
|
|
образом, |
|
|
|
|
|
|
|
Действительно,4 вероятностьюможет0вероятность.2,принять. . одно |
|||||||
|
|
|
|
|
|
|
то 0.5событиезначение. |
|
|
|
|||||||
|
|
|
|
|
|
вероятностью |
|
|
|
|
|
|
|||||
|
|
2 с вероятностью |
|
|
|
|
|
|
|
||||||||
значениеэтих значений |
|
|
F (x) = 0.7 |
|
|
|
|
U |
|||||||||
èç |
|
4 < x |
≤ 7 |
|
|
|
|
|
|||||||||
|
Åñëè |
|
|
|
|
|
|
|
|
|
|
0.5 + 0.2 = 0.7. |
|||||
его Такимр внаx1>. 7 |
òî Fискомая(x) = 1: ункция распределенияU ≤ 7 достоверноимеети вид |
||||||||||||||||
|
|
|
|
|
|
F (x) = 0.5 |
|
|
2 < x 4, |
||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
≤ 2, |
|||
|
ра ик ункции |
|
|
0.7 |
|
|
4 < x |
≤ 7, |
|||||||||
|
|
|
|
íà |
|
ïðè |
|
2. |
≤ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x > 7. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
рисунке |
|
|
|
|||
|
|
|
|
|
|
|
приведен |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
èñ. 2
Пример 2. Из 25 вопросов, включенных в программу экзамена,выбираетс у- дент подготовил 20. На экзамене студент случайным образом 5
20
