
besov
.pdf
§ 20.3. Формула Грина |
61 |
(ˆr(tj)), то прямоугольник Pj1 (Pjij ) можно сдвинуть параллельно оси Oy настолько, чтобы добиться его выполнения. Такая возможность основана на том, что в переходных точках 12 6 | tg α| 6 2, так что на [x0, x1] и на [xij−1, xij ] можно счи-
тать выполненной оценку 14 6 |ψ0| 6 4.
Пусть теперь кривая (11) не является контуром. Это означает, что ее начало и конец лежат на сторонах угловых прямоугольников (различных или одного и того же). Рассуждая так же, как в случае, когда кривая является контуром, построим для каждой ее дуги из (12) покрытие семейством прямоуголь-
ников {Pji}iij=1 со свойствами 1◦, 2◦, 3◦ и 4◦◦, 5◦, где последние два из них формулируются следующим образом:
4◦◦ каждая из концевых точек rˆ(tj−1), rˆ(tj) совпадает с вершиной одного из концевых прямоугольников, если касательная (j) в ней не параллельна ни одной из осей координат, и совпадает с серединой стороны одного из концевых прямоугольников, если касательная в ней параллельна одной из координатных осей;
5◦ int Pji не пересекаются ни с одним из угловых прямоугольников Qk.
Перенумеровав заново все построенные прямоугольники Pji для всех простых гладких дуг из ∂0D, получим семейство {Pj}mj=1 прямоугольников, попарно не имеющих общих внутренних точек, и таких, что
l ! m
[[
Qi Pj ∂D.
i=1 j=1
Проведем все прямые, содержащие все стороны всех прямоугольников Qi и Pj. Из образовавшихся таким образом (замкнутых) прямоугольников занумеруем и обозначим через Rk (1 6 k 6 r) те, которые пересекаются с D, но не имеют общих внутренних точек ни с одним из прямоугольников Qi и Pj. То-
гда Rk D. В самом деле, допустив, что в Rk имеются точки из D и из R2 \ D, на соединяющем их отрезке получим точку (x , y ) (∂D) ∩ int Rk. Следовательно, Rk имеет общую вну-

62 |
Глава 20. Криволинейные интегралы |
треннюю точку с тем прямоугольником Qi или Pj, который содержит точку (x , y ), а это противоречит построению Rk. Следовательно, D ∩ int Rk = int Rk — простая область.
Итак, показано, что
D |
|
Qi! |
|
|
|
|
|
Rk!, |
l |
m |
Pj |
|
r |
||||
|
[ |
|
[ |
|
|
k[ |
|
|
|
i=1 |
|
j=1 |
|
|
|
=1 |
|
где l + m + r прямоугольников попарно не имеют общих внутренних точек, пересечения D∩int Pj и D∩int Rk являются простыми областями, пересечение D∩int Qi либо является простой областью, либо может быть разрезано на две простые области.
Лемма доказана.
Заметим, что формула Грина имеет определенную аналогию с формулой Ньютона–Лейбница: интеграл от производных по области интегрирования выражается через значения функции на границе этой области.
Формулу Грина можно использовать для вычисления площади области с помощью криволинейного интеграла по ее границе. Для этого возьмем в качестве (P (x, y), Q(x, y))
(0, x) или |
− |
y |
, |
x |
|
или (−y, 0). |
||
|
|
|
|
|||||
2 |
2 |
|||||||
Тогда ∂Q∂x − ∂P∂y = 1 и по формуле Грина
Z Z Z
µD = x dy = 1 −y dx + x dy = − y dx. (13)
∂D+ 2 ∂D+ ∂D+
§ 20.4. Геометрический смысл знака якобиана плоского отображения
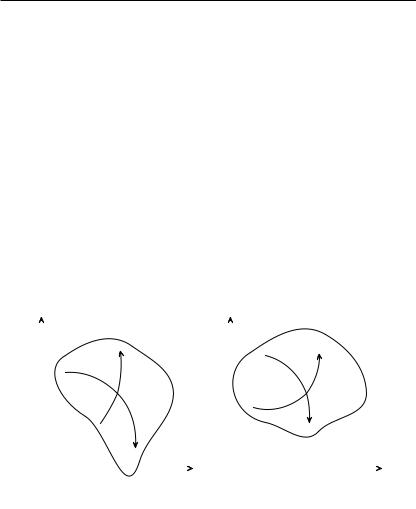
Изложим два подхода к выяснению геометрического смысла знака якобиана плоского отображения.
|
|
|
|
Первый подход |
k |
|
|
|
Для двух векторов |
|
|
~a = a1~ı + a2~|, |
||
|
||||
|
|
|
|
|
|
|
|
|
~ |
|
|
j |
b = b1~ı + b2~| |
|
|
|
|
||
i |
|
|||
Рис. 20.4 |
|
|||
§ 20.4. Геометрич. смысл знака якобиана плоск. отображения 63
из формулы |
|
|
|
|
|
~a ×~b = |
|
a1 b1 |
|
(~ı ×~|) |
|
a2 b2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sgn |
a1 b1 |
|
|
|
|
a2 b2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
показывает направление кратчайшего поворота от первого вектора ко второму. Именно при
a1 b1 |
|
> 0 (< 0) |
a2 b2 |
||
|
|
|
|
|
|
|
|
|
кратчайший поворот от к ~ производится в плоскости
~a b i, j
против (по) часовой стрелки.
v |
|
γ2 |
|
|
|
y |
|
|
Fγ2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F |
|
|
||
|
|
G |
|
|
|
−→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Fγ1 |
|
|
|
γ1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
u |
|
|
x |
||||
|
|
|
|
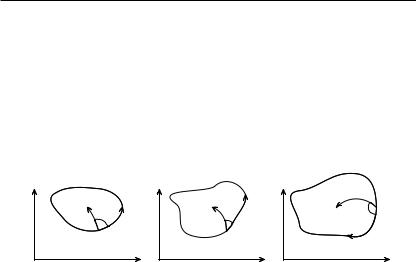
Рис. 20.5 |
|
|
||||
Пусть задано взаимно однозначное непрерывно дифферен- |
||||||||||
цируемое отображение |
|
(y = y(u, v) |
|
|
||||||
|
|
F |
: |
|
|
|||||
|
|
|
|
x = x(u, v), |
|
|
||||
области G плоскости |
(u, v), |
содержащей |
две пересекающи- |
|||||||
еся гладкие ориентированные кривые, на область в плоскости

64 |
Глава 20. Криволинейные интегралы |
(x, y) (см. рис. 20.5):
γ1 = {(u, v) : u = u1(t), v = v1(t)}, γ2 = {(u, v) : u = u2(t), v = v2(t)},
Fγ1 = {(x, y) : x = x1(t), y = y1(t)},
Fγ2 = {(x, y) : x = x2(t), y = y2(t)},
где
x1(t) B x(u1(t), v1(t)), y1(t) B y(u1(t), v1(t)),
x2(t) B x(u2(t), v2(t)), y2(t) B y(u2(t), v2(t)).
Будем считать, что в точке пересечения кривых γ1 и γ2 значение параметров t = t0. Сравним направление кратчайшего поворота касательного вектора к γ1 до касательного вектора к γ2 в точке пересечения кривых с соответствующим направлением для их образов F γ1, F γ2. Преобразуем для этого векторное произведение касательных векторов:
|
dx1 |
dx2 |
|
|
|
|
|
|
~ı + dy1 |
|
|
|
~ı + dy2 |
|
||
dy1 |
dy2 |
(~ı |
× |
~|) = |
|
dx1 |
~| |
dx2 |
~| = |
|||||||
|
dt |
dt |
|
|
|
dt |
|
dt |
|
× dt |
|
dt |
|
|||
|
dt |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=[(x0uu01 + x0vv10 )~ı + (yu0 u01 + yv0 v10 )~|] × [(x0uu02 + x0vv20 )~ı+ +(yu0 u02 + yv0 v20 )~|] = (x0uu01yv0 v20 + x0vv10 yu0 u02)(~ı ×~|)− −(x0uu02yv0 v10 + x0vv20 yu0 u01)(~ı ×~|) =
= (x0uyv0 − x0vyu0 )(u01v20 − v10 u02)(~ı ×~|).
Здесь было учтено, что ~| ×~ı = −~ı ×~|. Сравнивая коэффициенты при ~ı ×~| в левой и правой частях цепочки равенств, получаем
dx1
dt
dy1dt
dy2 |
|
= |
∂(u, v) v0 |
v0 . |
|||
dx2 |
|
∂(x, y) u0 |
u0 |
|
|||
dt |
|
|
|
|
1 |
2 |
|
|
|
|
1 |
2 |
|||
dt |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По столбцам определителей стоят координаты касательных векторов к γ1 и γ2 (правый определитель) и к Fγ1 и Fγ2 (левый определитель). Сравнивая знаки этих определителей, прихо-
дим к выводу: при ∂(x, y) > 0 (< 0) направление кратчайшего
∂(u, v)
поворота от первого касательного вектора ко второму после отображения сохраняется (меняется на противоположное).
§ 20.4. Геометрич. смысл знака якобиана плоск. отображения 65
Пусть теперь гладкая кривая γ1 является частью границы некоторой области D, замыкание которой содержится в G. Пусть γ1 ориентирована положительно относительно D. Сравним ориентацию γ1 относительно D и ориентацию 1 = F (γ1) относительно F (D). Возьмем кривую γ2, пересекающую γ1, с касательным вектором в точке пересечения, направленным по нормали к γ1 внутрь D. Из предыдущего видно, что возможны случаи ( i = F (γi)):
v |
|
y |
1 |
y |
|
γ2 |
|
2 |
2 |
|
|
γ1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
u |
J > 0 |
x |
J < 0 |
x |
|
|
|
|
||
|
|
Рис. 20.6 |
|
|
|
Таким образом, приходим к окончательной формулировке геометрического смысла знака якобиана плоского отображения.
При положительном якобиане сохраняется после отображения направление кратчайшего поворота от одной из пересекающихся кривых до другой, а также ориентация кривой, являющейся частью границы области D, относительно D.
При отрицательном якобиане указанные направления кратчайшего поворота и ориентация относительно области меняются на противоположные.
Второй подход
Этот подход основан на использовании формулы Грина. Пусть снова
(
x = (u, v),
F :
y= (u, v)
—взаимно однозначное непрерывно дифференцируемое ото-
бражение некоторой области G плоскости (u, v).
66 |
Глава 20. Криволинейные интегралы |
||||||
|
Пусть ограниченная область D |
|
G и якобиан |
||||
|
D |
||||||
|
|
∂(x, y) |
|
|
|||
|
J(u, v) B |
|
6= 0 на |
D. |
|||
|
∂(u, v) |
||||||
Тогда J(u, v) сохраняет знак на D, т. е. является либо положительным на G, либо отрицательным на G (см. теорему 10.5.4). Тогда D B F (D) также является ограниченной областью плоскости (x, y) (теорема 12.3.4).
Пусть B ∂D является простым кусочно гладким конту-
ром. Тогда
B F ( ) = F (∂D) = ∂D
(доказательство последнего равенства совпадает с доказательством утверждения 1◦ леммы 19.4.2) также является простым кусочно гладким контуром. В самом деле, пусть
i = {(u(t), v(t)) : a 6 t 6 b}
— гладкая кривая, i . Тогда
i B F ( i) = {(x(u(t), v(t)), y(u(t), v(t))), α 6 t 6 β}
является непрерывно дифференцируемой кривой по теореме о дифференцируемости сложной функции. Кроме того,
|
dx |
|
|
|
|
x0 |
du + x0 |
dv |
|
x0 |
x0 |
|
du |
|
|
|
|
|
||||||||
|
dt |
|
|
y |
u |
dt |
|
|
|
v |
dt |
= |
|
dt |
, |
|
|
|
||||||||
|
= |
|
+ y |
|
|
u |
|
|
v |
|
|
|
|
|||||||||||||
dy |
u0 |
du |
v0 |
dv |
y |
u0 |
y |
v0 |
dv |
|
|
|
||||||||||||||
dt |
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
! dt |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂(x, y) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6= 0. |
||
причем определитель квадратной матрицы равен |
|
|
||||||||||||||||||||||||
∂(u, v) |
||||||||||||||||||||||||||
Поэтому из |
du |
2 |
+ |
|
dv |
|
2 |
> 0 следует, что |
dx 2 |
+ |
dy |
2 > |
||||||||||||||
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
. |
dt |
|
|
dt |
|
||||
|
|
|
не имеет особых точек т е |
является гладкой |
||||||||||||||||||||||
> 0, т. е. что i |
|
|
|
|
|
|
|
|
|
|
|
, . |
|
|
|
|
|
. |
||||||||
Предполагая для определенности, что ориентация контура B |
||||||||||||||||||||||||||
B {(u(t), v(t)): |
a 6 t 6 b}, определяемая возрастанием пара- |
|||||||||||||||||||||||||
метра t, является положительной относительно D, так ориентированный контур обозначим через +. При этом ориентация контура = F ( ), наследуемая от ориентации контура+ (т. е. определяемая возрастанием параметра t), может оказаться как положительной, так и отрицательной относительно

§ 20.4. Геометрич. смысл знака якобиана плоск. отображения 67
области D = F (D). Контур с такой ориентацией относительно D обозначим через ±. В силу (20.3.13) имеем
|
Z |
|
|
|
|
|
|
Z b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
µD = |
± |
|
|
x dy = |
± |
|
xy0 |
dt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
± |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
b |
x ∂u dt |
+ ∂v dt |
dt = ± Z + x |
∂u du + x |
|
∂v dv. |
|||||||||||||||||||||
= ± Za |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
∂y du |
|
∂y dv |
|
|
|
|
|
∂y |
|
|
|
|
|
∂y |
|||||||||
Положим x ∂y = P , x ∂y = Q. Тогда |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
∂u |
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂Q |
|
∂x ∂y |
|
|
∂2y |
|
∂P |
|
∂x ∂y |
|
|
∂2y |
|
|
|
|
||||||||||||
|
|
= |
|
|
|
|
+ x |
|
|
, |
|
|
= |
|
|
|
|
+ x |
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
∂u∂v |
|
∂v |
∂v ∂u |
|
|
|
|
|
|
||||||||||||||
|
∂u |
|
∂u ∂v |
|
|
|
|
|
|
∂v∂u |
|
|
|
|
|||||||||||||||
Будем дополнительно предполагать, что на области G не- |
|||||||||||||||||||||||||||||
прерывны, а следовательно, и равны, производные |
|
∂2y |
|
, |
∂2y |
. |
|||||||||||||||||||||||
|
∂u∂v |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v∂u |
|||||
Применяя к последнему интегралу формулу Грина (20.3.3), получаем, что в зависимости от ориентации ±
|
|
∂P |
|
|
|||
µD = ± ZZD |
∂Q |
− |
du dv = ± ZZD |
∂(x, y) |
du dv. (1) |
||
∂u |
∂v |
∂(u, v) |
|
||||
В силу положительности левой части этой цепочки равенств положительна и правая часть, так что в области G
|
|
|
|
∂(x, y) |
|
|
|
|
∂(x, y) |
|
|
||||
|
± |
∂(u, v) |
= |
∂(u, v) |
> 0. |
|
|
+ |
|
|
|
|
|
|
ориентации кон- |
Рассматривая отдельно случаи |
различной |
||||||
тура (т. е. |
и −) и соответственно беря знаки в (1), |
||||||
приходим к следующему выводу. |
|
|
|
||||
В случае положительного якобиана при отображении ориентация граничного контура относительно области сохраняется, а в случае отрицательного якобиана — меняется на противоположную.
Отметим еще, что равенство (1) можно переписать в виде
RR |
) |
|
|
|
|
µD = |
|
∂(x, y) |
|
||
|
D |
(u, v) |
|
|
|
ланных здесь |
∂предположениях |
получено новое доказательство |
|||
формулы (19.5.11), |
из которой с помощью теоремы о среднем |
||||
вытекает и формула (19.4.3) (геометрический смысл модуля якобиана отображения).

68 Глава 20. Криволинейные интегралы
§ 20.5. Потенциальные векторные поля
Определение 1. Векторное поле ~a = (P (x, y, z), Q(x, y, z),
R(x, y, z)), заданное на области G R3, называется потенциальным в области G, если существует непрерывно дифференцируемая функция U: G → R такая, что
P = |
∂U |
, |
Q = |
∂U |
, |
R = |
∂U |
, на G. |
(1) |
|
∂x |
∂y |
∂z |
||||||||
|
|
|
|
|
|
|
Функцию U называют при этом потенциальной функцией поля ~a или потенциалом поля ~a.
Если функция U является потенциалом поля ~a, то функция U + C, где C — произвольная постоянная, также является потенциалом поля ~a.
Верно и обратное (что будет ясно из дальнейшего): если U, V — два потенциала поля ~a в области G, то V = U + C на G,
где C — некоторая постоянная. |
|
|
|||||||||
Равенства (1) иначе можно записать так: |
|
||||||||||
|
∂U |
∂U |
∂U ~ |
|
|
||||||
~a = |
|
~ı + |
|
~| + |
|
|
k = grad U = rU, |
(2) |
|||
∂x |
∂y |
∂z |
|||||||||
|
или |
dU = P dx + Q dy + R dz, |
|
||||||||
где r — символический вектор |
∂z , |
|
|||||||||
|
|
|
r = ∂x |
, ∂y , |
|
||||||
|
|
|
|
|
|
∂ |
|
∂ |
∂ |
|
|
называемый набла.
R
Интеграл (~a, d~r) по контуру называют циркуляцией векторного поля ~a по контуру .
Теорема 1. Пусть ~a = (P, Q, R) — непрерывное поле в области G. Тогда следующие условия эквивалентны:
I. Поле ~a потенциально в G.
II0. Для любого кусочно гладкого контура G
Z
(~a, d~r) = 0.

§ 20.5. Потенциальные векторные поля |
69 |
II00. Для любых двух фиксированных точек A, B G значение интеграла
|
|
|
|
|
|
ZAB |
(~a, d~r), |
|
|
где AB — произвольная кусочно гладкая кривая, лежащая в G
исоединяющая точки A и B, не зависит от кривой.
До к а з а т е л ь с т в о. Установим сначала, что II0 II00. Пусть выполнено II0 и +1 , +2 — две кривые, лежащие в G, начала которых находятся в точке A, а концы — в точке B.
Тогда в +1 −2 является ориентированным контуром и в силу
II0
ZZ
(~a, d~r) + |
(~a, d~r) = 0. |
1+ |
2− |
Заменив во втором интеграле ориентацию кривой −2 на противоположную на +2 , получаем
ZZ
+ (~a, d~r) − |
+ (~a, d~r) = 0, |
1 |
2 |
т. е. утверждение II00.
Пусть выполнено II00 и + G — произвольный кусочно
гладкий контур. Пусть точки A, B и кривые AB, BA являются дугами контура +, причем ориентация на каждой
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
, |
. |
|
. |
+ |
= |
||||||
из них совпадает с ориентацией контура |
|
|
т |
е |
|
|
AB |
|||||||||||||||||||
|
|
|
1 |
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
BA. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Через + AB |
и + = BA обозначим части контура + |
||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
той же ориентации, что и |
+: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
+ |
AB |
BA |
= + |
+. |
|
|
|
|
|
|
|
|
|
|||||||
|
Тогда 1+ и 2− — две кусочно гладкие кривые с началами |
|||||||||||||||||||||||||
в A и концами в B. В силу II00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Z + |
|
Z 1+ |
|
Z 2+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(~a, d~r) = |
(~a, d~r) + |
(~a, d~r) = |
|
(~a, d~r) − Z |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= Z |
|
(~a, d~r) = 0. |
|||||||||||
1+ |
2− |
70 |
|
Глава 20. Криволинейные интегралы |
|
|
|
||||
Покажем |
, |
что |
I II00. |
Пусть |
U — |
потенциал |
, |
|
|
|
|
|
|
AB = |
|||||
= {(x(t), y(t), z(t)), a 6 t 6 b} — кусочно гладкая кривая, лежащая в области G. Тогда
Z b
[P (x(t), y(t), z(t))x0(t)+
a
+Q(x(t), y(t), z(t))y0(t) + R(x(t), y(t), z(t))z0(t)] dt =
b d |
b |
||
= Za dt |
U(x(t), y(t), z(t)) dt = U(x(t), y(t), z(t)) a = |
||
|
|
|
|
|
|
|
|
|
|
|
|
= U(B) − U(A).
Покажем, наконец, что II00 I. Пусть точка A0 — фиксированная, а B(x, y, z) — произвольная точка области G. Рассмотрим функцию
|
|
|
|
(3) |
0 |
|
U(B) = U(x, y, z) B ZA0B P dx + Q dy + R dz, |
||
|
|
|
||
где A B — кусочно гладкая кривая, лежащая в G. Такое опре- |
||||
деление функции U корректно, т. к. правая часть (3) в силу II00 |
||||
зависит лишь от B(x, y, z), т. е. от (x, y, z). Поэтому правую |
||||
часть (3) нередко записывают в виде B P dx + Q dy + R dz. |
||||
R
A0
Покажем, что U является потенциалом поля ~a, т. е. выполняются равенства (1), из которых установим лишь первое. Пусть B0 = B0(x0, y0, z0) G. Установим равенство
|
∂U |
(x0, y0, z0) = P (x0, y0, z0) |
|
(4) |
|
∂x |
|
||
|
|
|
|
|
непосредственным вычислением производной |
∂U . |
Пусть |
||
|
|
|
∂x |
|
|
|
|
||
U(x0, y0, z0) и U(x0 + x, y0, z0) представлены в виде (20.3.3) с
помощью соответственно кривых A0B0 и A0B B A0B0 B0B, где B0B — отрезок, соединяющий точки B0 и B. Тогда
U B U(x0 + x, y0, z0) − U(x0, y0, z0) =
|
|
x |
+Δx |
= Z |
|
P dx + Q dy + R dz = Zx0 0 |
P (x, y0, z0) dx. |
BB0 |
При получении последнего равенства использовано определение криволинейного интеграла через определенный интеграл
