Metody_optimizatsii

43

Замечани е2. О бновлени еметода,

какправи ло, прои зводи тся и для

зачастую

сопровождается вы чи сли тельны ми погреш ностями .

П р имер . Н айти методом сопряжённы х гради ентов точку ми ни мума

функц и и

2

2

4

3+ x , нача4x(=-x)впои+сxксточкx иf xx0

=

) .0,(0

Р ешение.

1

2

1

1

2

Ñf (x)=(8x1-4x2+1;6x2-4x1).

И т ерация1.

0.

Задади м ε =0,01, x0=(0,0), Ñf (x0 ) = (1,0), ||Ñf (x0 ) ||=1.

1.

Положи м к =0, p0= -Ñf (x0 ) =(-1,0).

2.

Реш и м задачу одномерной ми ни ми зац и и по α :

2α α ® α- .

=minF -

α 0=1/8.

Ñf (x1 ) = (0,1/2),

1 ||

3.

Н айдем х1=х0+ α 0 p0=(-1/8,0),

)1/2Ñ(> ε ||.f =x

4.

k + 1 ¹ n

2

0

1

2

5.

β0

Ñ

x

||

f || =)=1/4Ñ(f . x ||

|| ) (

p1= -Ñf (x1 ) + β0 p0=(-1/4,-1/2).

И т ерация2.

2.

Реш и м задачу одномерной ми ни ми зац и и по α :

( 1/8

α 4 , α

4(1/8

α 2 )

34α)

2

4(1/8 α

4 ())α 22 -

+

-

1/8

α

4 ®- min-.

при води тся к еди ни чной (т. е.

T

= E ),QтоHQметод наи скорейш его спуска

х1 Q−1 =х0 Q−1 - α *Ñf (x0 ) Q

и ли

х1 =х0- α *Ñf (x0 ) Q Q−1 .

Т аккак Q Q−1 =H-1 , то

х1 =х0- α *Ñf (x0 )

H-1. И терати вны й метод ви да

хk+1 =хk- α k Ñf (xk ) H-1

носи тназвани еметодаН ью тона.

Д ля квадрати чной функц и и

с положи тельно определенной матри ц ей

44

х0 вы брана недостаточно бли зко к

опти мальному

реш ени ю ,

то

последовательностьхk можетрасходи ться (каки водномерном случае).

Сущ ественны м недостатком метода

Н ью тона является необходи мость

вы чи слени я и обращ ени я матри ц ы Гессенакаждой и терац и и .

П р имер . Н айти методом Н ью тонаточку ми ни мумафункц и и

( )

2

2

+ x

1

, начаx =-xвпои4 +сx3ксточкx 4иf x0

=x ( ,0)0.

1

2

1

2

æ

8

− 4

ö

М атри ц авторы х частны х прои зводны х и меетви д H=ç

÷ .

ç

- 4

6

÷

è

ø

-1

1

æ

6

4

ö

Н айдем обратную матри ц у H

=

ç

÷ .

32

ç

4

8

÷

è

ø

0. В ы берем ε =0.001, 0 =x ( ,0)0,

f(x0)=0.

0

0

0

-1

1

0

2.

Положи м х

=х

- Ñf (x

) H

=

− 8)1, -f(x=,16)= −33

(326() 4,

32

3.

Ñf (x0 ) =(0,0) -найдено опти мальноереш ени е x*= −

− (8)1.

3 ,16

Ц елевая функц и я квадрати чная, поэтому реш ени езадачи получено заодну

и терац и ю .

З а да чи для са мо сто ятельно го р еш ения

1. Н айти разли чны ми методами точку ми ни мумаследую щ и х функц и й:

2

2

1

2

0

= 0)1 , ( x+ x, -2= x +4

x 2

x 1x))f (

1

2

2

2

1

0

= 3)5, ( x=- x,+ 12

x

x 2 ))2x( f

1

2

2

2

1

2

0

= 10) 5, (- x

-= x, 4x+ x 2

x 3x))f (

1

2

2

2

1

2

0

= 5)4, ( x-

x-=, 2

+x 4

x

x 4x))f (

1

2

2

2

1

2

0

= ,0)0 ( x - x, -32= +x 6

x 4

x ))5x( f

1

2

2

2

1 2

0

= 2)1, ( x=- x,+ x

x

x 2 6x))f (

1

2

2

2

1 2

0

= 0)2, ( x -= x, x+2

x3

x 7x))f (

1

2

45

2. Показать, что для квадрати чной

функц и и вметодеН ью тонаш аг

α* = 1.

§ 6. Ч исленны е мето ды

по иска усло в но го

экстр емума

В §2 бы ли рассмотрены необходи мы еи достаточны еуслови я

реш ени я

задачнели нейной

условной опти ми зац и и ви да

f (x) → min

j

≤

=

;

m, 1 j

, 0 xg) (

g x

j

, 1 + p=. +m, 0=( )m j

И спользовани е данны х

услови й

при води т

к

необходи мости

реш ени я

сложны х си стем равенств и

неравенств.

А нали ти чески

реш и ть получаемы е

си стемы возможно только для ограни ченного чи слапри меров. Д ля реш ени я

больш и нства

практи чески х

задач

и спользую тся

чи сленны е

методы .

Ч и сленны еметоды можно условно раздели тьнатри группы .

1.

М ет оды

возмож ных

направлений.

Э то

методы

непосредственного

реш ени я задачи условной опти ми зац и и ,

основанны енадви жени и

и з одной

допусти мой xk точки кдругой допусти мой точке x k +1 с"лучш и м" значени ем

ц елевой функц и и . Д ви жени еосущ ествляется по прави лу

+

=

k

k 1

k

x

+ α k yx .

В

качестве вектораy k

вы би рается возможное и

подходящ ее направлени е

пои ска в точке xk , а ш аг

α k

вы би рается,

напри мер, путем опти ми зац и и

ц елевой

функц и и

в

данном

направлени и

по αk . К

данны м

методам,

напри мер, относятся:

мет оды проекции градиент а и

мет оды возмож ных

направлений.

2.

М ет оды линеаризации. Д анны е методы

основаны

на сведени и

задач

нели нейной

условной

опти ми зац и и

к

задачам

ли нейной

условной

опти ми зац и и

на уровне и сходной

постановки

с дальнейш и м

анали зом

полученны х результатови корректи ровкой реш аемой ли нейной задачи.

3.

М ет оды последоват ельной безусловной минимизации. В

основе данны х

методов

лежи т

преобразовани е

задачи

условной

опти ми зац и и

в

последовательность задач безусловной

опти ми зац и и

путем введени я

в

рассмотрени е

вспомогательны х

ц елевы х

функц и й.

И сходная

задача

аппрокси ми руется

некоторой последовательностью вспомогательны х задач

безусловной

ми ни ми зац и и ,

для

которы х

разработаны

эффекти вны е

и

надежны е методы

реш ени я. Последовательность вспомогательны х

задач

подби рается, как прави ло, таки м образом,

чтобы

реш ени е и сходной задачи

оказы валось

пределом

последовательности

получаемы х

реш ени й

вспомогательны х задач. Ч асто,

для получени я реш ени я и сходной задачи

с

требуемой точностью

достаточно бы вает реш и ть относи тельно небольш ое

чи сло вспомогательны х

задач. В спомогательны е задачи

можно реш ать

при бли женны ми

методами

и

и нформац и ю ,

полученную

в результате

47

Замети м,

что

если

в

задаче отсутствую т

ограни чени я-равенства

и

в рассматри ваемой

точке x

нет акти вны х

ограни чени й

(т.е.

точка x

является внутренней),

то в качествеподходящ его направлени я можно взять

y = -Ñf (x) .

В

проти вном

случае

построени е подходящ и х

направлени й

можно осущ естви ть в ви де ми ни ми зац и и

функц и и

Ñ ( )T y fпрxи

услови ях

1

≤

,

= 0 .

О Cyднако 0Aеслyи

сущ ествует такой

вектор y, такой, что

Ñ ( )

T

< 0f, x

y

≤

,

= 0 , тоCyми ни мальное0A y

значени ефункц и и

Ñf (x) yT

1

при такой ми ни ми зац и и

несущ ествует(

f x)y(TÑ

-¥inf), ®таккаклю бой

вектор λy ,

где λ

-

сколь угодно больш ое чи сло,

также удовлетворяет

услови ям

1λ

≤

,

λ

= 0 . ТyакиCм образомA0 y ,

в задачу ми ни ми зац и и должно

бы ть вклю чено услови е, которое ограни чи вало бы

вектор y,

напри мер,

услови е

£ ,

=

.1И yтаi к, 1возможноеи подходящ еенаправлени еи щ ется

i

, n

вви де реш ени я следую щ ей задачи ли нейного программи ровани я

Ñ

fyTx® min

( )

1

≤

,

= 0

Cy

0A y

− ≤ i ≤ 11,

y =

.1

i, n

А лго р итм

Ш аг 1. Задатьначальную

точку x0,

характери сти ку точности алгори тма

ε > 0. Положи тьk = 0 .

Ñf (xk )

Ш аг 2.

Н айти

Ñf (xk ) .

Е сли

£ ε ,

то вы чи слени я прекрати ть и

положи ть x* = xk , и начеперейти кш агу 3.

Ш аг 3. Подстави ть xk

в неравенстваи определи тьмножество и ндексов

акти вны х ограни чени й I (xk ) .

Ш аг4. Е сли

I (xk ) = Æ и взадаченетограни чени й равенств, то положи ть

k

=y-Ñ (xkf) ,

и наче

определи ть

y k

и з

реш ени я

задачи

ли нейного

программи ровани я

k

T k

Ñ

y

f

)(

)(

x® min

1

k £ ,

k = 0

Cy

0 A y

ik £ 1-1, £y =

.1

i, n

Ш аг5. Е сли Ñ

k

T

k

, то задачарешy f x

енаточно и

x

*

= x

k

. И наче -

)(

=)(0

для найденного вектора y k

определи ть

α k =

min

k

k

). f

x

(arg + α y

α: xk +α ykÎW

Ш аг6. Н айти очередноепри бли жени е

+

=

k

k

1

k

x

+ α k

yx .

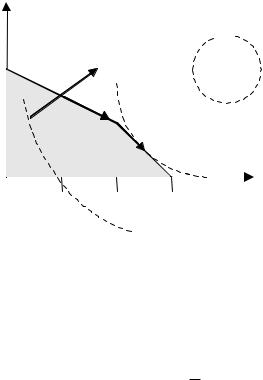
П р имер 1. Реш и тьрассмотренны м методом следую щ ую

задачу

1

2

2

2

2 ®x min- 4

+=x)

-yf x( )

( )( ,

1 +

2 ≤ x3,

x

48

2 +

2 £ 4x,

x2

1 ,

2 ³ 0x.

x

Реш ени е.

1

17

x0

æ

ö

1.

В озьмем в качественачальной точки

= ç

,

÷. Л егко провери ть, что

2

12

è

ø

Положи м ε = 0,01,

данная точка при надлежи т допусти мому множеству.

k = 0 .

И зобрази м графи чески допусти мое множество и ли ни и уровня

ц елевой функц и и

3

x2

x

.

1

.

1

..

(4,2)

x0 .

x2

0

1

2

3

x1

0

æ

7

ö

Ñf (xk )

> ε , то перейдем кш агу 3.

2.

Н айдем

ç 7Ñ,-

(÷-f. Тx=)аккак

è

6 ø

3.

В сеограни чени я вы полняю тся в точке x0

как строги е неравенства, т.е.

x0 -

внутренняя

точка допусти мого множества. Поэтому I (x0 ) = Æ .

Полагаем 0

0

æ

7 ö

=

ç7y,

(÷=. -x)Ñf

è

6 ø

4.

О пределяя α0 и з соотнош ени я

æ

7

ö2

æ

7

7

ö2

1

α0 =

min

ç7αarg-

÷

+

ç