
Основы теории информации и передачи сигналов
.pdf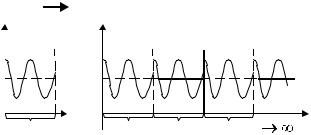
26 |
Теория информации и передачи сигналов |
При этом
X |
|
S(un ,2X ) = ∫s(x) exp(− j2πun x) dx , |
(36) |
−X |
|
т.е. финитное преобразование Фурье связано с коэффициентами An |
ряда Фу- |
рье, а именно: |
|
S(un ,2X ) = 2An X . |
|
Иначе говоря, финитное преобразование Фурье сводится к нахождению коэффициентов ряда Фурье для функции s(x), периодически продолженной с периодом L = 2X (рис. 1.7). При нецелом числе периодов, укладывающихся на отрезке L, происходит искажение спектра.
Периодическое
продолжение
s(x) |
|
s(x) |
|
|
|
s0 |
|
s0 |
|
|
|
0 |
x |
0 |
|
|
x |
L |
L |
L |
L |
Рис. 1.7. Трансляция отрезков сигнала ограниченной протяженности
Математическое описание систем передачи и обработки сигналов
В системах передачи и обработки сигналов осуществляется преобразование входных сигналов sвх в выходные sвых . Характеристики преобразования
могут быть заданными (например, при фильтрации сигналов) или должны быть исследованы (например, при анализе характеристик линий передачи информации). Во всех случаях используются основные положения теории систем.
Наиболее важными являются линейные системы, подчиняющиеся принципу суперпозиции:
T{αsвх1 +βsвх2 } = αT{sвых1 } +βT{sвых2 } , |
(37) |
где α и β – постоянные, T – оператор системы. |
|

1. Основы теории информации и теории сигналов |
27 |
Импульсной характеристикой (реакцией) системы, по определению, называется функция
h(x) = T{δ(x)} , |
(38) |
где δ(x) – дельта-функция. Обычно независимой переменной x является вре-
мя.
Систему называют стационарной или инвариантной во времени, если при выполнении условия
sвых (x) = T{sвх (x)} |
(39) |
следует, что
sвых (x −χ) = T{sвх (x −χ)} ,
где χ - произвольный сдвиг.
Импульсная характеристика инвариантной во времени системы с учетом (38), очевидно, подчиняется соотношению
h(x −χ) = T{δ(x −χ)} .
Входной сигнал можно представить последовательностью дельтафункций:
∞ |
|
sвх (x) = ∫sвх (χ) δ(x −χ) dχ , |
(40) |
−∞ |
|
∞ |
|
где ∫δ(χ) dχ =1 . |
|
−∞ |
|
Сигнал на выходе системы из (38) – (40) определяется выражением |
|
∞ |
|
sвых (x) = T{sвх (x)} = ∫sвх (χ) T{δ(x −χ)} dχ . |
|
−∞ |
|
В результате выходной сигнал определяется интегралом свёртки |
|
∞ |
|
sвых (x) = ∫sвх (χ) h(x −χ) dχ = sвх (x) h(x) . |
(41) |
−∞ |
|
Пусть существует преобразование Фурье сигнала F{s(x)} = S(u) |
и им- |
пульсной характеристики системы F{h(x)} = H (u) . Используя свойства преобразования Фурье, можно доказать теорему о свёртке (30):
F |
|
s(x) h(x) S(u)H (u) . |
|
Поскольку sвых (x) = sвх (x) h(x) , то в спектральной области |
|
Sвых (u) = Sвх (u) H (u) . |
(42) |
Функция |
|
H (u) = Sвых (u) Sвх (u) |
(43) |
называется частотной характеристикой системы.
28 |
Теория информации и передачи сигналов |
Детерминированные и стохастические сигналы
Преобразование Фурье (21) содержит полную информацию о сигнале s(x) в частотном представлении. Если сигнал s(x) является реализацией случайного процесса {s(x)}, то результат преобразования (21) будет изменяться от сигнала к сигналу («от опыта к опыту»). Неизменной характеристикой ансамбля реализаций {s(x)} стационарного эргодического случайного процесса является спектральная плотность
Gs (u) = lim (1 X ) Sk (u,2X ) 2 |
, |
(44) |
X →∞ |
|
|
где угловые скобки обозначают усреднение по ансамблю реализаций (индексу k). Спектральная плотность характеризует значение среднего квадрата процесса: площадь под графиком спектральной плотности на произвольном частотном интервале (u1,u2 ) равна среднему квадрату процесса в этой поло-
се частот. Наряду с понятием спектральной плотности часто используют со-
ответствующее понятие энергетического спектра.
Спектральная плотность стационарного эргодического случайного про-
цесса связана с корреляционной функцией |
Rs (χ) этого процесса преобразо- |
||
ванием Фурье: |
|
|
|
|
|
∞ |
|
Gs (u) = F{Rs (χ)} ∫Rs (χ) exp(− j2πuχ) dχ, |
(45) |
||
где |
|
−∞ |
|
|
|
|
|
|
|
∞ |
|
Rs (χ) = |
lim (1 X ) ∫s(x) s(x + χ) dx . |
(46) |
|
|
X →∞ |
0 |
|
|
|
|
|
Соотношение (45) носит название теоремы Винера-Хинчина. Поскольку автокорреляционная функция (46) является чётной функцией, спектральная плотность (45) является действительной чётной функцией.
Таблица 1. Основные величины и типичные единицы их измерения
Величина |
Обозначение |
Единица измерения |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Сигнал |
|
|
|
s(x) |
В (Вольт) |
|||||
2. Амплитудный спектр (АС) |
|
|
|
S(u, X ) |
|
|
В с |
||||
|
|
||||||||||
3. |
Квадрат модуля АС |
|
S(u, X ) |
|
2 |
В2 |
с2 |
||||
|
|
||||||||||
4. |
Спектральная плотность |
|
|
|
Gs (u) |
В2 |
с = В2 Гц |
||||
5. |
Корреляционная функция |
|
|
|
Rs (u) |
В2 |
|
||||
1. Основы теории информации и теории сигналов |
29 |
1.6. Принципы дискретизации непрерывных сигналов
Пусть функция s(x) определяет исходный непрерывный сигнал. Операция дискретизации заключается в выполнении преобразования вида
sˆ(x) = d(x) [s(x) h(x)] ,
где в простейшем случае апертурная функция элемента дискретизации h(x)
имеет вид
h(x) = rect(x 2b) = 1, |
| x | < b, |
(47) |
0, |
| x | ≥ b, |
|
2b – ширина элемента дискретизации,
d(x) = d0 K∑−1δ(x −k∆x)
k =0
– функция дискретизации, ∆x – шаг дискретизации, d0 – нормирующий мно-
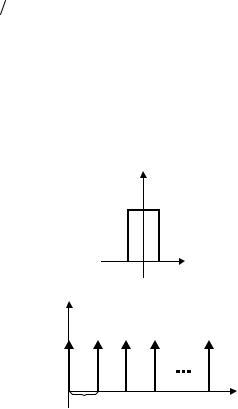
житель, такой, что площадь под графиком d(x) равна единице. Вид функций h(x) и d(x) иллюстрируются на рис. 1.8.
h(x) |
а) |
1 |
|
-b 0 |
b x |
d(x) |
б) |
|
δ(x-k∆x) |
0 ∆x |
k∆x (K-1)∆x x |
Рис. 1.8. Прямоугольная функция элемента дискретизации (а) и функция дискретизации (б)
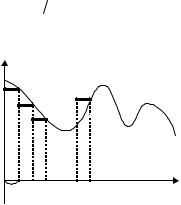
Сигнал s(x) можно представить последовательностью импульсов протяженностью 2b = ∆x , имеющих амплитуды, равные значениям сигнала в точ-
30 |
Теория информации и передачи сигналов |
ках (k +1) ∆x . Тогда получим ступенчатую функцию, показанную на рис. 1.9, а именно
ˆ |
= |
∞ |
∆ |
− ∆ |
+∆ |
(48) |
s(x) |
|
∑s(k x) h(x |
k x |
x 2) . |
||
|
|
k =0 |
|
|
|
|
s(x)
0 ∆x |
∆ |
x |
k∆x (k+1) x |
|
|
Рис. 1.9. Ступенчатая аппроксимация непрерывного сигнала |
||
После перехода к пределу при ∆x → 0, получим |
|
|
∞ |
|
|
sˆ = ∫s(ξ) h(x −ξ) dξ = s(x) h(x) . |
(49) |
|
0 |
|
|
Такое преобразование является операцией свертки, которая имеет следующие важные свойства:
дистрибутивность
a(x) [b(x) +c(x)] = a(x) b(x) +a(x) c(x)
коммутативность a(x) b(x) = b(x) a(x)
ассоциативность
[a(x) b(x)] c(x) = a(x) [b(x) c(x)] = a(x) b(x) c(x) .
Подчеркнем, что при условии существования интеграла (49) операция свертки не вносит ограничений на вид апертурной функции элемента дискретизации h(x).
Процесс дискретизации удобно рассматривать в частотном представлении, получаемом в результате преобразования Фурье исходного сигнала. Функция дискретизации определяется в частотной области следующим выражением:
1. Основы теории информации и теории сигналов |
31 |
∞
D(u) = F{d(x)} = ud ∑δ(u −kud ) , (50)
k =0
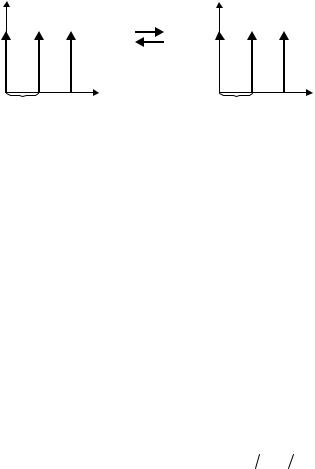
где F{.} обозначает операцию преобразования Фурье, ud =1 (∆x) . Вид
(∆x) . Вид
функции D(u) показан на рис. 1.10. Таким образом, процесс выборки дискретных значений сигнала вызывает появление спектральных порядков kud , k ≥1.
d(x) |
|
D(u) |
|
|
... |
F |
... |
|
|
||
0 ∆x |
x |
0 ud |
u |
Рис. 1.10. Функция дискретизации и её частотное представление
Дискретизованный сигнал имеет вид произведения двух функций, поэтому, согласно теореме о свертке, его спектр равен свертке спектров:
ˆ |
|
|
S(u) = S(u) D(u) . Поскольку с учетом (50) и свойств частотной симметрии |
||
преобразования Фурье (см. разд 1.5) можно записать, что |
||
ˆ |
∞ |
|
∑δ(u −kud ) , |
||
S(u) = S(u) ud |
||
|
k =−∞ |
|
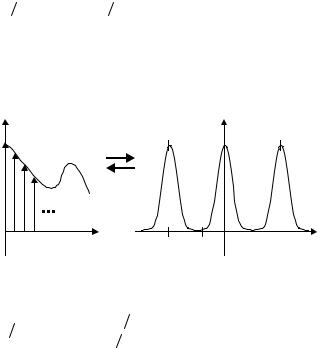
спектр дискретизованного сигнала представляет собой спектр исходного сигнала, периодически повторенного (перенесенного) по частотной оси с шагом ud , как это иллюстрируется на рис. 1.11, включая диапазон отрицательных
частот.
Теорема дискретизации формулируется следующим образом:
Для того, чтобы спектр исходного сигнала в области частот (−uM ;uM ) не
искажался в процессе дискретизации, необходимо и достаточно выполнение неравенства ud ≥ 2uM , где uM – наибольшая частота в спектре синала.
Спектр сигнала, очевидно, можно выразить в форме
ˆ |
∞ |
|
|
∑S(u −kud ) . |
(51) |
||
S(u) = ud |
|||
|
k =−∞ |
|
|
Выделим из этого спектра частотный интервал (−ud |
2;ud 2) и выполним |
||
обратное преобразование Фурье. В результате получим |
|
||
32 |
Теория информации и передачи сигналов |
∞ |
|
s(x) = ∑s(k ud ) sinc[ud (x −k ud )]. |
(52) |
k =−∞ |
|
Отсюда следует теорема Шеннона: если для частоты дискретизации ud |
|
справедливо неравенство ud ≥ 2uM , |
то сигнал s(x) восстанавливается одно- |
значно по его дискретным значениям s(k ud ), k = 0,±1,...
ud ), k = 0,±1,...
s(x) |
S(u) |
F
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x |
|
−ud −u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
M 0 u |
|
M u |
|
d |
u |
|||||||||||||
|
|
|
|
|||||||||||||||||
Рис. 1.11. Формирование спектра при дискретизации сигнала |
||||||||||||||||||||
Функция |
sin[πud (x −k ud )] |
|
||||||||||||||||||
sinc[ud (x −k ud )] = |
|
|||||||||||||||||||
πud (x |
−k ud ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
называется интерполяционной функцией Шеннона. |
|
|||||||||||||||||||
Дискретизация узкополосных сигналов |
|
|||||||||||||||||||
Модель типичного узкополосного сигнала имеет вид |
|
|||||||||||||||||||
s(x) = s0 (x) + sm (x) cos(ε + 2πu0 x) + n(x) , |
(53) |
|||||||||||||||||||
где s0 (x) – фоновая составляющая, |
sm (x) – огибающая, изменяющиеся мед- |
|||||||||||||||||||
ленно по сравнению с периодом 1 u0 , ε – начальная фаза в точке x = 0, u0 –
u0 , ε – начальная фаза в точке x = 0, u0 –
частота, n(x) – аддитивный шум. В результате дискретизации получаем сигнал
sˆ(x) = d(x) [s(x) h(x)] ,
при этом спектр сигнала определяется выражением
ˆ |
* |
(u −u0 ) + N (u)] H (u) . |
(54) |
F{sˆ(x)} = S(u) = D(u) [S0 |
(u) + S1 (u −u0 ) + S1 |
Здесь N(u) обозначает амплитудный спектр аддитивного шума, H(u) – преобразование Фурье апертурной функции элемента дискретизации. Для функции
1. Основы теории информации и теории сигналов |
33 |
вида (47) прямоугольной формы и ∆x = 2b нулевые значения H(u) имеют место на частотах us =1 (2b) .
(2b) .
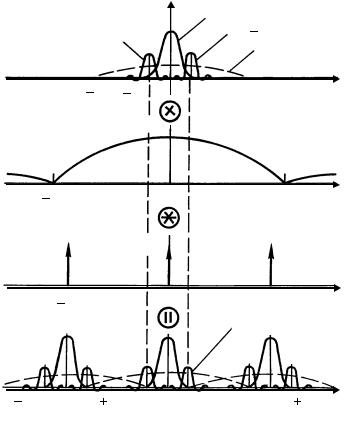
Спектр дискретизованного сигнала имеет вид, показанный на рис. 1.12. При обработке спектра обычно выделяют составляющую S1 (u −u0 ) .
S1* (u +u0 )
Bn u0 0
|H(u)|
us |
0 |
D(u)
ud |
0 |
S0 (u)
S1(u Nu(0u))
u0 |
Bn |
u |
us
ud
S1 (u-u0 )
ud |
|
u0 |
|
ud u0 |
|
u0 0 u0 |
ud |
|
u0 ud u0 |
|
|
|
|
Рис. 1.12. Формирование спектра при дискретизации узкополосного сигнала
Рассмотрим методику выбора шага дискретизации узкополосного сигнала. Если частота u0 гармонической составляющей априорно известна, то шаг
дискретизации ∆x определяется согласно теореме дискретизации, а именно, нужно выполнить условие u0 < (1 2∆x) , т.е. ∆x <1
2∆x) , т.е. ∆x <1 2u0 . Таким образом, шаг
2u0 . Таким образом, шаг

34 |
Теория информации и передачи сигналов |
дискретизации должен быть меньше половины периода гармонического сигнала.
Если сигнал s(x) не является строго гармоническим и имеет протяженный спектр с граничной частотой uM , то выбор шага дискретизации определяется
по теореме дискретизации: ∆x <1 2uM .
2uM .
Для уменьшения влияния спектра шума, попадающего из соседних спектральных порядков (рис. 1.12), нужно настолько уменьшить шаг дискретизации, чтобы он не превышал значения 1 (2unM ) , где unM – составляющая шу-
ма с наибольшей частотой. Следует иметь в виду, что вследствие стохастического характера шума можно строго определить его спектр мощности, но не амплитудный спектр. Поэтому результат преобразования Фурье шума может существенно изменяться от реализации к реализации. Некоррелированный шум имеет спектр бесконечной протяженности. Поэтому перед дискретизацией сигнала необходимо выполнить низкочастотную фильтрацию для получения «окрашенного» шума с граничной частотой unM ≤ ud  2 .
2 .
Влияние формы элемента дискретизации
Операция дискретизации определяется формулой sˆ(x) = d (x) [s(x) h(x)].
Выше был рассмотрен случай ступенчатой аппроксимации нулевого порядка, как это показано на рис. 1.9. Функция h(x), вообще говоря, может иметь произвольную форму. Однако в любом случае нужно иметь в виду, что форма и протяженность функции h(x) влияют на спектр сигнала за счет умножения спектра этого сигнала на функцию H (u) = F{h(x)} (рис. 1.12).
Приведем простой пример. Пусть h(x) = rect(x 2b) . Соответствующая функция в спектральной области будет равна
2b) . Соответствующая функция в спектральной области будет равна
H (u) = sinc(2ub) = sin(2πub) .
В этом несложно убедиться непосредственным интегрированием функции косинуса:
b π = sin(2πub) (1 2b) ∫ cos(2 ux) dx .
−b
Поэтому составляющие спектра сигнала при u > 0 будут ослаблены вплоть до полного подавления на частоте us =1 2b (рис. 1.12).
2b (рис. 1.12).
Таким образом, можно сделать следующие выводы.
1. Основы теории информации и теории сигналов |
35 |
Влияние размера элемента дискретизации на спектральную составляющую с частотой u тем меньше, чем меньше отношение 2b T , где T =1
T , где T =1 u –
u –
период этой составляющей.
Во избежание энергетических потерь при дискретизации непрерывного сигнала уменьшение размера элемента дискретизации должно сопровождаться соответствующим повышением частоты дискретизации.
