
Лекция № 3
.pdfИндекс х у символа дисперсии означает, что этот показатель характеризует варьирование числовых значений признака вокруг их средней величины.
Ценность дисперсии заключается в том, что, являясь мерой варьирования числовых значений признака вокруг их средней арифметической, она измеряет и внутреннюю изменчивость значений признака, зависящую от разностей между наблюдениями. Преимущество дисперсии перед другими показателями вариации состоит в том, что она разлагается на составные компоненты, позволяя тем самым оценивать влияние различных факторов на величину учитываемого признака.
Вместе с тем установлено, что рассчитываемая по формуле (1336),
дисперсия оказывается смещенной по отношению к своему генеральному параметру на величину, равную n/(n-1). Чтобы получить несмещенную дисперсию, нужно в формулу (13) ввести в качестве множителя поправку на смещенность, называемую поправкой Бесселя. В результате формула (36)
преобразуется следующим образом:
k
(xi x )2
sx2 |
i |
|
(37). |
|
n 1 |
||
|
|
|
Разность n-1, обозначаемую в дальнейшем строчной буквой k,
называют числом степеней свободы, под которым понимают число свободно варьирующих единиц в составе численно ограниченной статистической совокупности.
Так, если совокупность состоит из n-го числа членов и характеризуется средней величиной x , то любой член этой совокупности может иметь какое угодно значение, не изменяя при этом среднюю x , кроме одной варианты,
значение которой определяется разностью между суммой значений всех остальных вариант и величиной nx . Следовательно, одна варианта численно ограниченной статистической совокупности не имеет свободы вариации.
Отсюда число степеней свободы для такой совокупности будет равно ее объему n без единицы, т.е. k=n-1. А при наличии не одного, а нескольких

ограничений свободы вариации число степеней свободы будет равно k=n- ,
где - обозначает число ограничений свободы вариации.
Среднее квадратическое отклонение sx показывает, насколько выборочные значения разбросаны относительно среднего. Этот показатель представляет собой корень квадратный из дисперсии:
k
(xi x )2
sx |
i |
|
(38). |
|
n 1 |
||
|
|
|
Эта величина в ряде случаев является более удобной характеристикой варьирования, чем дисперсия, поскольку выражается в тех же единицах, что и средняя арифметическая величина.
Дисперсия и среднее квадратическое отклонение наилучшим образом характеризуют не только величину, но и специфику варьирования признаков.
При одинаковых лимитах и размахе вариации дисперсия и среднее квадратическое отклонение могут оказаться неодинаковыми: на величине этих показателей сказывается различный характер варьирования признака.
Коэффициент вариации V, Cv. Дисперсия и среднее квадратическое отклонение применимы для сравнительной оценки одноименных средних величин. В практике же довольно часто приходится сравнивать изменчивость признаков, выраженных разными единицами. В таких случаях используют не абсолютные, а относительные показатели вариации. Дисперсия и среднее квадратическое отклонение как величины, выражаемые теми же единицами,
что и характеризуемый ими признак, для оценки изменчивости разноименных величин непригодны. Одним из относительных показателей вариации является коэффициент вариации. Этот показатель представляет собой среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической:
Cv |
sx |
100% |
(39) |
|
|||
|
x |
|
|
Пример. Сравнивают два варьирующих признака. Один характеризуется средней x =2,4 кг и средним квадратическим отклонением sx=0,58 кг, другой — величинами х=8,3 см и sx=1,57 см. Следует ли отсюда,
что второй признак варьирует сильнее, чем первый? Нет, не следует, так как среднее квадратическое отклонение определяют по отклонениям от средних, а они различны по величине. Кроме того, не вполне корректно сравнивать величины, выраженные разными единицами меры. Именно поэтому в подобных случаях уместно использовать безразмерные значения коэффициентов вариации. Сравнивая их в приводимом примере, находим,
что сильнее варьирует не второй, а первый признак:
Cv =100(0,58/2,4) =24,2% и Cv = 100 (1,57/8,3) = 18,9%.
Различные признаки характеризуются различными коэффициентами вариации. Но в отношении одного и того же признака значение этого показателя Cv остается более или менее устойчивым и при симметричных распределениях обычно не превышает 50%. При сильно асимметричных рядах распределения коэффициент вариации может достигать 100% и даже выше. Варьирование считается слабым, если не превосходит 10%, средним,
когда Cv составляет 11-25%, и значительным при Cv 25%.
Применяя коэффициент вариации в качестве характеристики варьирования, следует учитывать единицы размерности изучаемого признака: линейные или весовые (объемные). В таких случаях коэффициент вариации оказывается неодинаковым. При линейном выражении величины признака коэффициент вариации оказывается примерно в три раза меньше,
чем при кубическом выражении того же признака. Причина такого явления – в математических свойствах Cv, которые надо учитывать, чтобы избежать возможных ошибок.
Нормированное отклонение t. Отклонение той или иной варианты от средней арифметической, отнесенное к величине среднего квадратического отклонения, называют нормированным отклонением:
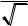
t |
xi x |
(40) |
|
|
sx |
Этот показатель позволяет «измерять» отклонения отдельных вариант от среднего уровня и сравнивать их для разных признаков.
Получая значения нормированных отклонений для разных признаков,
можно сравнивать места, занимаемые особью, индивидом и т.п. по каждому из этих признаков в их распределениях.
Пример. При обследовании группы подростков в возрасте от 15 до 16
лет установлено, что средний рост юношей характеризуется следующими показателями: x =164,8 см и sx=5,8 см. В группе оказался юноша, рост которого равен 172,4 см. Спрашивается: как велико отклонение роста этого юноши от средней величины данного признака в этой группе? Нормируя рост юноши ( x =172,4), находим t=(172,4-164,8)/5,8=+1,31.
Получая значения нормированных отклонений для разных признаков,
можно сравнить места, занимаемые особью, индивидом и т. п. по каждому из этих признаков в их распределениях. Пусть, например, нормированное отклонение у рассматриваемого юноши по ширине плеч равно 0,41. Тогда можно утверждать, что у него длина тела отклоняется от средней в сторону больших величин этого признака, а ширина плеч — в сторону малых, т. е.
характерен относительно узкоплечий тип телосложения.
Нормированное отклонение используют при работе с так называемым нормальным распределением.
Форма представления результатов исследования.
В биомедицинских публикациях вместе со средним арифметическим очень часто указывают так называемую стандартную ошибку среднего,
обозначаемую обычно т и вычисляемую по формуле:
m |
sx |
, |
(41) |
|
n |
||||
|
где sx — выборочное стандартное отклонение, а n — число измерений
(или наблюдений). Стандартная ошибка среднего стремится к нулю при
увеличении числа измерений. Использование стандартной ошибки среднего пришло в статистику из физики, где при измерении параметров одинаковых объектов (например, заряда электрона) вариабельность получаемых значений определяется только случайными погрешностями. Увеличивая n, мы все точнее знаем реальное значение измеряемого параметра. При увеличении числа измерений улучшается качество проверки статистических гипотез.
Исследователю же нужно выяснить, в какой диапазон укладывается большинство значений определяемого параметра, т.е. охарактеризовать ширину
распределения.
Ширину нормального распределения принято характеризовать
стандартным отклонением (синоним — среднее квадратичное отклонение),
точнее, выборочным стандартным отклонением, поскольку обычно мы работаем с выборочными распределениями.
В отличие от m, sx не уменьшается при увеличении п, но определяется более точно. Результаты представляют как x sx; в диапазон x sx
укладываются около 70% значений нормального распределения.
К сожалению, стандартное отклонение плохо приспособлено для описания распределений, отличных от нормального, в особенности асимметричных распределений. Для возрастной зависимости средний возраст заболевания x sx пришлось бы записать как 5±15 лет, в то время как очевидно, что отрицательных возрастов не существует.
Из непараметрических характеристик ширины распределения наиболее адекватные — это квантили или перцентили.
Итоги измерений (наблюдений) могут быть представлены в виде тройки цифр: нижний квартиль — медиана — верхний квартиль, дающих представление о центральной тенденции, ширине и асимметрии распределения результатов. К сожалению, этот простой и безотказный подход пока не получил достаточного распространения в русскоязычной литературе.
Оценка ширины распределения в виде x sx или нижний квартиль — медиана — верхний квартиль позволяет выбрать правильный формат представления данных. Если, как это обычно бывает в биомедицине, sx
составляет более 10% от x , или интерквартильный интервал более 10% от медианы, то величины x (или Ме) и sx (или интерквартильный интервал)
записываются с точностью не более 2 значащих цифр.
Выборочная оценка генеральных параметров
Числовые показатели, характеризующие генеральную совокупность,
называются параметрами, а числовые показатели, характеризующие выборку, – выборочными характеристиками или статистиками.
Выборочные характеристики являются приближенными оценками генеральных параметров. Эти величины случайные, варьирующие вокруг своих параметров. Оценки генеральных параметров по выборочным характеристикам могут быть точечными или интервальными.
Точечные оценки генеральных параметров
Генеральные характеристики принято обозначать буквами греческого алфавита, а выборочные характеристики – латинского. Выборочная средняя x является оценкой генеральной средней , выборочная дисперсия sx2 –
оценкой генеральной дисперсии x2, а среднее квадратическое отклонение sx
– оценкой стандартного отклонения x, характеризующего генеральную совокупность. Это точечные оценки, представляющие собой не интервалы, а
числа («точки»), вычисляемые по случайной выборке.
Точечные оценки должны удовлетворять следующим требованиям:
быть состоятельными, эффективными и несмещенными.
Точечная оценка называется состоятельной, если при увеличении объема выборки она стремиться к величине генерального параметра.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с
другими аналогичными оценками, т.е. обнаруживает наименьшую случайную вариацию.
Точечная оценка называется несмещенной, если математическое ожидание ее выборочного распределения совпадает со значением
генерального параметра.
Выборочные характеристики, как правило, не совпадают по абсолютной величине с соответствующими генеральными параметрами.
Величину отклонения выборочного показателя от его генерального
параметра называют статистической ошибкой, или ошибкой
репрезентативности. Статистические ошибки присущи только выборочным характеристикам, они возникают в процессе отбора вариант из генеральной совокупности.
Из теории математической статистики известно, что в том случае,
когда распределение исходного признака не слишком сильно отличается от нормального, а объем выборки не слишком мал (n 30), квадратческая ошибка репрезентативности средней арифметической может быть найдена по
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
sx |
|
s |
x |
|
|
s2 x |
(51), |
|||
|
|
|
n |
||||||||
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
|
x |
sx |
|
|
s |
x |
|
s2 |
|
||
при n 30 |
|
|
x |
|
(52). |
||||||
|
|
|
n 1 |
||||||||
n |
1 |
||||||||||
|
|
|
|
|
|
|
|||||
Статистические ошибки характеризуют варьирование выборочных показателей вокруг своих генеральных параметров. Они обладают теми же свойствами, что и среднее квадратическое отклонение. Чем сильнее варьирует признак, тем больше при прочих равных условиях будет ошибка выборочных показателей, и, наоборот, при слабом варьировании признака ошибка выборочных показателей окажется меньше. Одно лишь свойство специфично для ошибок репрезентативности: они уменьшаются при увеличении объема выборки, т. е. при n , sx 0. Это свойство

статистических ошибок обусловлено действием закона больших чисел, по которому наиболее вероятный результат получается при наибольшем числе испытаний. Отсюда понятно значение ошибки: она указывает на точность, с
какой выборочный показатель репрезентирует генеральный параметр. Чем меньше ошибка, тем ближе выборочная характеристика к величине генерального параметра, и, наоборот, чем больше ошибка, тем менее точно выборочная характеристика репрезентирует генеральный параметр.
Судить о точности, с которой определена та или иная выборочная средняя, позволяет отношение ошибки репрезентативности к своей средней.
Этот показатель, обозначаемый символом Cs, определяют по формуле:
|
Cs |
|
|
Cv |
(53), |
|||
|
|
|
|
|
||||
|
|
|
n |
|||||
|
|
|
|
|
|
|
||
где |
Cv |
|
sx |
100% |
(54). |
|||
|
||||||||
|
|
|
x |
|
|
|
|
|
Здесь Cv – коэффициент вариации, выраженный в процентах, n – объем выборки.
Показатель точности Cs нашел широкое применение. Точность средних показателей, которыми оценивают результаты наблюдений, считают вполне удовлетворительной, если коэффициент Cs не превышает 3 – 5%.
Интервальные оценки генеральных параметров. Доверительный
интервал
По известным выборочным характеристикам можно построить интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей,
называют доверительными. Понятие о доверительных вероятностях предложено Р. Фишером. Оно вытекает из принципа, который положен в основу применения теории вероятностей к решению практических задач.
Согласно этому принципу, маловероятные события считаются практически
невозможными, а события, вероятность которых близка к 1, принимают за почти достоверные. Обычно в качестве доверительных используют вероятности Р1 = 0,95; Р2 = 0,99 и Р3 = 0,999. Это означает, что при оценке генеральных параметров по известным выборочным показателям существует риск ошибиться в первом случае один раз на 20 испытаний, во втором – один раз на 100 испытаний и в третьем – один раз на 1000 испытаний.
Доверительным вероятностям соответствуют следующие величины нормированных отклонений:
Вероятности Р1 = 0,95 соответствует t1=1,96.
Вероятности Р2 = 0,99 соответствует t2=2,58.
Вероятности Р3 = 0,999 соответствует t3=3,29.
Выбор того или иного порога доверительной вероятности исследователь осуществляет, исходя из практических соображений той ответственности, с какой делаются выводы о генеральных параметрах.
С доверительной вероятностью тесно связан и уровень значимости ,
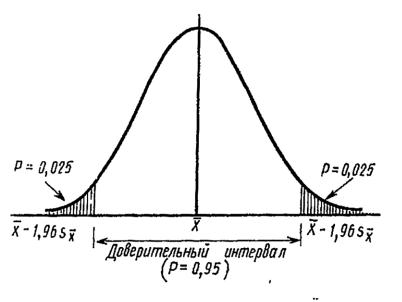
под которым понимают разность =1–Р. Геометрически эта величина представляет собой площадь под кривой выборочного распределения некоторой статистики, выходящую за пределы той его части, которая включает Р % его площади (рис. 34).

Рис. 34. 95 %-ный доверительный интервал в границах от x - 1,96sx до x +1,96sx нормальной кривой
Так, для t=1,96 отклонения от центра нормального распределения включают 95% его площади. За пределами этих границ по обе стороны находится по 2,5% указанной площади, составляя тем самым 5%-ный уровень значимости.
Учитывая, что выборочное среднее распределение некоторой статистики при достаточно больших объемах выборок имеет нормальную форму, можно записать выражение:
t |
x |
t |
(55) |
|
|||
|
sx |
|
|
Это выражение обозначает, что вероятность того, что средняя |
x , |
||
найденная по выборке, отклониться случайным образом от центра на
какую-то долю квадратической ошибки sx , может быть оценена через нормированное значение по таблицам нормального распределения. Отсюда можно утверждать, что генеральная средняя находится с этой вероятностью в интервале
x tsx x tsx |
(1); |
x |
ts |
x |
|
x |
ts |
x |
|
|
(2). |
||
|
|
|
|
|
|
||||||
n |
n |
||||||||||
|
|
|
|
|
|
|
|||||
Величины x и sx определяют по |
выборке, а |
t зависит только от |
|||||||||
значения доверительной вероятности.
Наиболее типичный случай оценки доверительного интервала — представление результатов измерения некоторой количественной величины в виде «среднее арифметическое 95% доверительный интервал». На самом деле, не только для среднего, но и для любой, точно неизвестной случайной величины можно попытаться оценить область значений, в которой эта величина находится с вероятностью, не меньшей заданной (например 95%).
