Лекция № 3

Рис. 23. Полигон распределения частот

Линия, соединяющая вершины перпендикуляров, называется

вариационной кривой, или кривой распределения частот вариационного ряда.

Рис. 24. Вариационная кривая

При построении интервального вариационного ряда по оси абсцисс откладывают границы классовых интервалов, по оси ординат – частоты интервалов. В результате получается гистограмма распределения частот.

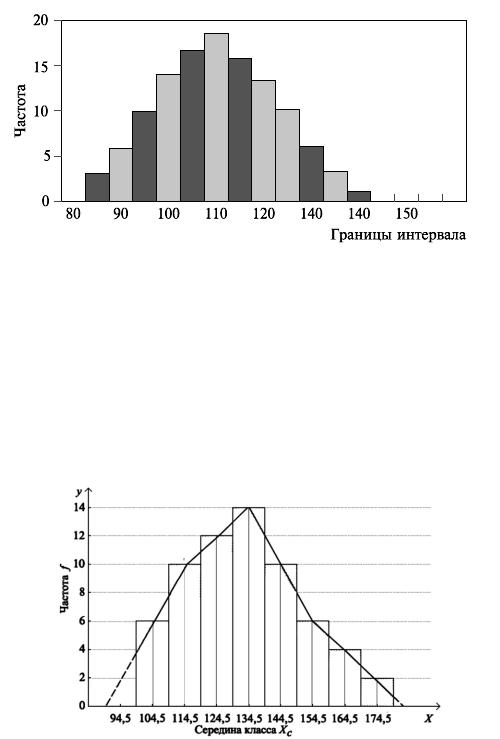
Рис. 25. Гистограмма распределения частот

Если из середин верхних сторон прямоугольников гистограммы опустить перпендикуляры на ось абсцисс, гистограмма превращается в полигон распределения, а линия, соединяющая середины верхних сторон прямоугольников гистограммы, будет представлять собой вариационную кривую.

Рис. 26. Графики вариационных рядов

Неумелое построение графиков приводит к тому, что они получаются либо островершинными с узким основанием, либо плосковершинными,

чрезмерно растянутыми по оси абсцисс. Избежать этих недостатков позволяет правило «золотого сечения», согласно которому основание геометрической фигуры должно относиться к ее высоте как 1 : 0,62.

Применительно к построению вариационной кривой масштабы на осях следует выбирать с таким расчетом, чтобы основание кривой было в 1,5 – 2

раза больше ее высоты. Откладывая по оси абсцисс классы вариационного ряда, следует доводить крайние из них до нулевых классов, в которых не содержится ни одной варианты. В результате вариационной кривой придается законченный, хорошо обозримый вид.

Параметры совокупности, характеризующие центральную

тенденцию ряда. Средние величины

Для полного описания варьирующих объектов служат особые,

логически и теоретически обоснованные числовые показатели, называемые

статистическими характеристиками. К ним относят, прежде всего, средние величины и показатели вариации.

Вотличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать целую группу однородных единиц одним (средним) числом. Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее среднее и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один объект от другого.

Вкачестве статистических характеристик применяют степенные и

структурные (нестепенные) средние величины.

Степенные средние вычисляют из общей формулы:

где М – средняя величина; xi – варианта, n – число наблюдений, для которых вычисляют среднюю; k – величина, по которой определяют вид средней. Так при k=1 получается средняя арифметическая, при k=2 – средняя квадратическая, при k=-1 – средняя гармоническая и т.д.

Из структурных средних в биологии используют медиану, моду и т.д.

Пример. Пять доярок в течение 1 ч (60 мин) надоили следующее количество молока: первая—10 л, вторая — 20, третья — 25, четвертая — 30

и пятая — 20 л; всего 105 л за 1 ч. Оценим эти итоги с помощью x и xh Получим следующие результаты: x = (10+20+25+30+20) :5=21 л;

определить общее количество надоенного пятью доярками молока: 21·5=105 л.

Попробуем с помощью x вычислить время, затраченное в среднем одной

дояркой на выдаивание 1 л молока. Получим результат: 60/21 = =2,86 мин/л.

Верно ли это? Проверим результат: первая доярка на выдаивание 1 л

молока затратила 60/10=6 мин, вторая— 60/20=3, третья — 2,4, четвертая

— 2, пятая — 3 мин. В среднем получается (6+3+2,4+2+3)/5= 16,4/5=3,38

мин/л. Видно, что средняя арифметическая непригодна для определения среднего времени, затрачиваемого на выдаивание 1 л молока. Другой результат получается с применением средней гармонической: 60:18,31 = 3,28

мин/л. Это точный результат.

Средняя квадратическая xq. Для более точной числовой характеристики мер площади применяется средняя квадратическая. Этот

показатель вычисляют по формуле:

Средняя кубическая xQ. В качестве характеристики объемных признаков более точной является средняя кубическая, определяемая по

формулам:

Средняя геометрическая xg. Этот показатель представляет собой корень n-ной степени из произведений членов ряда:

где n – объем совокупности; при этом xi 0.

Средняя геометрическая применяется в тех случаях, когда изменения вариант в ряду происходят в геометрической прогрессии, т.е. каждый последующий уровень ряда, характеризующий развитие явления, примерно равен предыдущему, умноженному на некоторое постоянное для данной прогрессии число. Изменение явлений в геометрической прогрессии имеет место в микробиологической и иммунологической практике (размножение микроорганизмов, нарастание титра антител и т. д.)

Однако средняя геометрическая, как правило, незначительно отличается по величине от средней арифметической. К тому же вычисление средней арифметической проще, чем средней геометрической. Поэтому вместо средней геометрической в качестве приближенной характеристики темпов динамики нередко используют среднюю арифметическую. При этом приходится учитывать, что средняя геометрическая дает хорошие (не искаженные) результаты лишь при наличии геометрической прогрессии,

заложенной в самой динамике явления. Это обстоятельство несколько ограничивает область применения средней геометрической, которую вычисляют обычно в прогностических целях и при определении средних прибавок массы или размеров тела, возрастных изменений численного состава популяций за определенные (обычно равные) промежутки времени.

Между степенными средними существуют определенные соотношения,

выражаемые следующим рядом мажоратности: xQ xq x xg xh.

Средняя арифметическая – одна из основных характеристик варьирующих объектов по тому или иному признаку. Однако она не лишена недостатков, так как очень чувствительна к увеличению числа наблюдений или к уменьшению за счет вариант, резко отличающихся по своей величине

от основной массы. Поэтому на величину средней арифметической могут значительно влиять крайние члены ранжированного вариационного ряда,

которые как раз наименее характерны для данной совокупности.

Поэтому прежде чем приступить к вычислению средней арифметической, необходимо убедиться в отсутствии в вариационном ряду так называемых «выскакивающих» вариант, или выбросов, которые в значительной степени могут искажать конечные результаты.

Выбросы значительно отличаются по величине от других вариант и нетипичны для данного ряда. Как правило, они являются следствием ошибочных записей или погрешностей в экспериментальных исследованиях.

Если установить достоверно причину появления «выскакивающей» варианты невозможно, ее исключают из вариационного ряда путем расчетов.

Практически не приходится прибегать к исключению минимальных значений вариант, так как даже резкое отличие их от других существенно не влияет на значение средних величин.

Во многих случаях в качестве обобщающих характеристик совокупности более полезными могут оказаться так называемые

структурные средние. Эти величины обычно представляют собой конкретные варианты имеющейся совокупности, которые занимают определенное место в ряду распределения.

Медиана (Ме) представляет собой значение, которое делит выборку пополам: число выборочных значений, меньших Ме (m), равно числу выборочных значений, больших Ме (m). При симметричном распределении значений переменной значение выборочного среднего близко к значению медианы. При наличии небольшого числа вариант медиана определяется довольно просто. Для этого собранные данные ранжируют, и при нечетном числе членов ряда центральная его варианта и будет медианой. При четном числе членов ряда медиана определяется по полусумме двух соседних вариант, расположенных в центре ранжированного ряда. Для данных,

сгруппированных в вариационный ряд, медиана определяется по следующей формуле:

где хн – нижняя граница классового интервала, содержащего медиану, или полусумма соседних классов безынтервального ряда, в промежутке между которыми находится медиана; fi – сумма накопленных частот, стоящая перед медианным классом; fMe – частота медианного класса; - величина классового интервала; n – общее число наблюдений.

Мода (Мо) - это величина, наиболее часто встречающаяся в данной совокупности. Класс с наибольшей частотой называется модальным. Он определяется довольно просто в безынтервальных рядах:

где хн – нижняя граница модального класса, т.е. класса с наибольшей частотой f2; f1 – частота класса, предшествующего модальному; f3 – частота класса, следующего за модальным; - величина классового интервала.

Квантили – это значения вариант, отсекающие в пределах ряда определенную часть его членов. Квартили представляют собой три значения признака, делящие ранжированный вариационный ряд на 4 части.

Аналогично, 9 децилей делят ряд на 10 равных частей, а 99 перцентилей – на

100 равных частей.

Разобьем весь диапазон значений, которые принимает переменная, на десять интервалов так, чтобы в первый диапазон попали наименьшие значения (10% от общего количества) и так далее. В последний диапазон попадут 10% наибольших значений. Границы между интервалами называются, соответственно, 10%, 20% ... 90% квантилями. Вне интервала от

10% до 90% квантиля оказывается 20% наиболее отклоняющихся значений.

Часто весь диапазон значений разбивают только на четыре интервала,

получая, соответственно, 25%, 50% и 75% квантили; 25% и 75% квантили называют также нижним и верхним квартилями. 50% квантиль — это, как нетрудно заметить, медиана. Внутри интерквартильного интервала лежат

50% наиболее типичных (близких к центральному) значений.

В практике используют обычно перцентили Р3, Р10, Р25, Р50, Р75, Р90, Р97. Причем Р25 и Р75 соответствуют первому и третьему квартилям, между которыми находится 50% всех членов ряда, а Р50 соответствует второму квартилю. Любой перцентиль определяется рядом последовательных действий, которые можно выразить в виде следующей формулы:

где хн – нижняя граница класса, содержащего перцентиль Рj, она определяется по величине K = Ljn /100, превосходящей или равной fi в ряду накопленных частот; Рj – выбранный перцентиль; n – общее число наблюдений; - ширина классового интервала; fp – частота класса,

содержащего искомый перцентиль; Lj – так называемый порядок перцентиля,

показывающий, какой процент наблюдений имеет меньшую величину, чем

Рj.

Таким образом, как и при определении медианы, нахождение того или иного перцентиля связано с кумуляцией частот вариационного ряда в направлении от низшего (начального) класса к высшему.

Параметры совокупности, характеризующие варьирование

признака

Средние величины не являются универсальными характеристиками варьирующих объектов. При одинаковых средних признаки могут отличаться по величине и характеру варьирования. Поэтому наряду со средними для характеристики варьирующих объектов используют показатели вариации.