
- •§1. Метрическая проекция в гильбертовом пространстве.
- •§2. Многозначные отображения. Основные свойства.
- •§3. Метрическая проекция в баннаховым пространстве.
- •3.1. Метрическая проекция на компактное множество.
- •3.2. Метрическая проекция на замкнутое множество.
- •§4. Некоторые приложения метрической
- •4.2. Неподвижные точки многозначных
4.2. Неподвижные точки многозначных
Сжимающих отображений.
Пусть
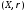 -полное
метрическое пространство;
-полное
метрическое пространство;
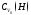 ,
как и прежде, обозначает совокупность
всех непустых замкнутых ограниченных
подмножествX;h– метрика Хаусдорфа в
,
как и прежде, обозначает совокупность
всех непустых замкнутых ограниченных
подмножествX;h– метрика Хаусдорфа в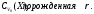
4.2.1.
Определение. Многозначное отображение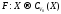 называется
к-липшецевым, если существует число к
называется
к-липшецевым, если существует число к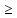 0
такое, что для любых х, у
0
такое, что для любых х, у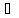 Х
выполнено неравенство
Х
выполнено неравенство
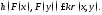
Если к < 1, то к-липшецего многозначное отображение Fназывается сжимающим (к- сжимающим).
4.2.2. Теорема.ЕслиF– сжимающее
многозначное отображение, то оно имеет
по крайней мере одну неподвижную точку,
то есть точку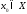 такую,
что
такую,
что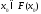 .
.
Пусть Н –
гильбертово пространство,
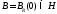 -
замкнутый шар с границей
-
замкнутый шар с границей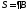 .
.
4.2.3. Лемма.Если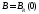 ,
то для любой точки
,
то для любой точки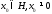 точка
точка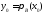 представляется
в виде
представляется
в виде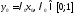 .
.
Доказательство.Возможны два случая:
1)Если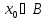 ,
то
,
то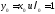 .
.
2)Пусть
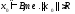 .
Предположим
.
Предположим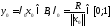 .
Согласно лемме 1.9
.
Согласно лемме 1.9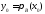 тогда и только тогда, когда для любого
тогда и только тогда, когда для любого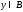 выполняется неравенство
выполняется неравенство
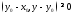 .
Докажем это неравенство для точки
.
Докажем это неравенство для точки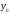 .
Тогда
.
Тогда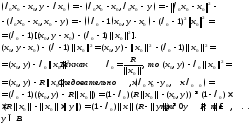
Лемма доказана.
Пусть
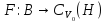 -
многозначное сжимающее отображение,
-
многозначное сжимающее отображение,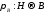 .
Пусть
.
Пусть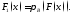
4.2.4. Лемма.Отображение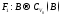 является
многозначным сжимающим отображением.
является
многозначным сжимающим отображением.
Доказательство.Так как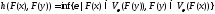 ,
выполнено включение
,
выполнено включение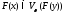 .
Это означает, что для любой точки
.
Это означает, что для любой точки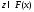 существует
точка
существует
точка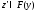 такая,
что
такая,
что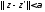 .
В силу теоремы 1.10 выполняется неравенство
.
В силу теоремы 1.10 выполняется неравенство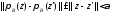 .
Тогда для любой
.
Тогда для любой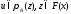 найдется
найдется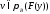 такая,
что
такая,
что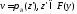 .
Откуда
.
Откуда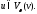 Следовательно,
Следовательно,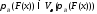 .
.
Аналогично
доказывается, что из включения
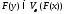 следует
следует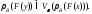
Таким
образом, получим неравенство
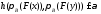 .
Следовательно, в силу свойств метрики
Хаусдорфа будет выполнено неравенство
.
Следовательно, в силу свойств метрики
Хаусдорфа будет выполнено неравенство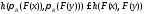 .
Так как отображение Так как отображение
-сжимающее, то существует число
.
Так как отображение Так как отображение
-сжимающее, то существует число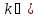 ,
для которого справедливо
,
для которого справедливо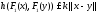 ,
то есть отображение
,
то есть отображение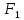 сжимающее.
Лемма доказана.
сжимающее.
Лемма доказана.
4.2.5. Теорема.Пусть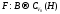 -
многозначное сжимающее отображение
такое, что
-
многозначное сжимающее отображение
такое, что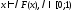 для
любой точки
для
любой точки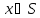 .
Тогда
.
Тогда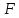 имеет неподвижную точку.
имеет неподвижную точку.
Доказательство.Пусть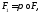 тогда
в силу теоремы 4.2.2 существует точка
тогда
в силу теоремы 4.2.2 существует точка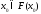 .
Возможны два случая.
.
Возможны два случая.
Пусть
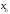 является неподвижной точкой отображенияF. Если это выполнено, то
теорема доказана.
является неподвижной точкой отображенияF. Если это выполнено, то
теорема доказана.Пусть x
 является неподвижной точкой
является неподвижной точкой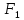 .
Предположим, что х
.
Предположим, что х не является неподвижной точкойF,
то есть
не является неподвижной точкойF,
то есть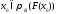 и
и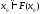 .
Тогда существует точка
.
Тогда существует точка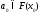 такая, что
такая, что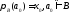 ,
так как в противном случае
,
так как в противном случае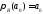 .
.
Тогда в силу леммы 4.2.3 существует
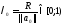 такое,
что
такое,
что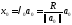 ,
следовательно,
,
следовательно,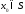 .
Тогда
.
Тогда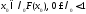 ,
что противоречит условию теоремы.
Теорема доказана.
,
что противоречит условию теоремы.
Теорема доказана.
