
- •§1. Метрическая проекция в гильбертовом пространстве.
- •§2. Многозначные отображения. Основные свойства.
- •§3. Метрическая проекция в баннаховым пространстве.
- •3.1. Метрическая проекция на компактное множество.
- •3.2. Метрическая проекция на замкнутое множество.
- •§4. Некоторые приложения метрической
- •4.2. Неподвижные точки многозначных
3.2. Метрическая проекция на замкнутое множество.
Пусть У – баннахово пространство.
3.2.1.
Определение.Совокупность всех
непрерывных линейных функционалов образует линейное пространство, которое
называется пространством, сопряженным
с Е, и обозначается
образует линейное пространство, которое
называется пространством, сопряженным
с Е, и обозначается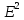 .
.
Пространство
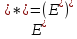 ,
сопряженное к
,
сопряженное к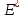 ,
- это есть совокупность всех линейных
непрерывных функционалов на
,
- это есть совокупность всех линейных
непрерывных функционалов на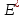 .
.
Поскольку
можно каждый элемент из Е рассматривать
еще и как элемент пространства
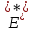 ,
удобно для значений линейного функционала
,
удобно для значений линейного функционала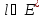 вместо записи
вместо записи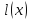 ввести обозначение:
ввести обозначение: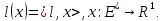
Рассмотрим
каноническое вложение
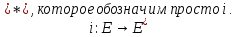
3.2.2.
Определение.Банахово пространство
Е называется рефлексивным, если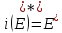 ,
т.е. Е изометрично
,
т.е. Е изометрично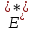 при каноническом вложенииi.
при каноническом вложенииi.
3.2.3.
Определение.Последовательность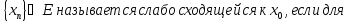
Любого
линейного функционала
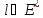 последовательность чисел
последовательность чисел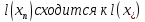 .
.
3.2.4. Теорема.В рефлексивном банаховом пространстве любое ограниченное замкнутое выпуклое множество является слабо компактным.
3.2.5. Лемма
(Мазура).Пусть Е – рефлексивное
банахово пространство, С – замкнутое
выпуклое множество в Е, последовательность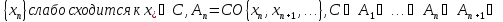 …
Тогда существует последовательность
…
Тогда существует последовательность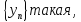 что выполняются следующие условия: 1)
что выполняются следующие условия: 1)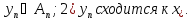
3.2.6. Теорема.Пусть Е – рефлексивное банахово
пространство, С – замкнутое выпуклое
множество в Е. Тогда для любой точки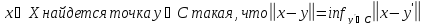 .
.
Доказательство.Пусть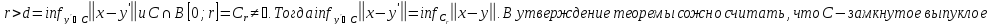
 .
Возьмем минимизирующую последовательность
.
Возьмем минимизирующую последовательность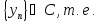
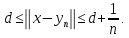 Так как
Так как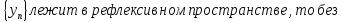
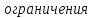 общности
можно считать, что
общности
можно считать, что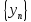 слабо сходится к
слабо сходится к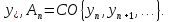 В силу леммы Мазура найдется
последовательность
В силу леммы Мазура найдется
последовательность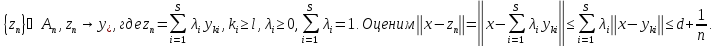 В полученном неравенстве
В полученном неравенстве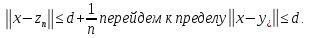 Теорема доказана.
Теорема доказана.
Возникает
отображение

3.2.7. Лемма.Для любого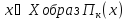 является ограниченным выпуклым замкнутым
множеством.
является ограниченным выпуклым замкнутым
множеством.
Доказательство.Выпуклость и замкнутость множества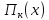 доказывается аналогично теореме 3.1.3.
доказывается аналогично теореме 3.1.3.
Представляет
интерес изучение непрерывности
многозначного отображения
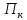 .
.
§4. Некоторые приложения метрической
Проекции.
4.1 . Непрерывное сечение многозначного отображения
В Гильбертовом пространстве.
Пусть Х –
метрическое пространство,
 -
непрерывное по Хаусдорфу многозначное
отображение.
-
непрерывное по Хаусдорфу многозначное
отображение.
4.1.1. Определение.
Однозначное
отображение
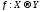 называется
сечением многозначного отображенияF,
если
называется
сечением многозначного отображенияF,
если
f(X)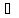 F(X) для
каждой точкиx
F(X) для
каждой точкиx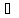 X.
X.
Докажем теорему о существовании сечения отображения F.
Возьмем
точку D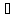 Н
и определим отображение
Н
и определим отображение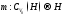 по
следующему правилу: для любого
по
следующему правилу: для любого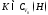 выполнено
выполнено
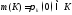 ,
т.е.m(K) –
это точка К такая, на которой реализуется
кратчайшее расстояние до нуля пространстваH.
,
т.е.m(K) –
это точка К такая, на которой реализуется
кратчайшее расстояние до нуля пространстваH.
4.1.2. Лемма.
Для любых

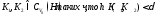 ,
гдеh– метрика Хаусдорфа,
выполняется неравенство
,
гдеh– метрика Хаусдорфа,
выполняется неравенство
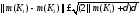 .
.
Доказательство.
По определению
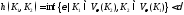 .
Это означает, что
.
Это означает, что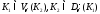 .
Для любой
.
Для любой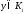 найдется
точка
найдется
точка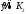 такая,
что
такая,
что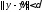 и для любой
и для любой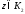 найдется
точка
найдется
точка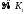 такая, что
такая, что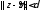 .
Обозначим
.
Обозначим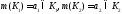 .
Тогда для
.
Тогда для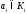 найдется точка
найдется точка ,
,
для
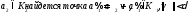 .
.
Воспользовавшись леммой 1.6 получим
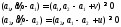
Откуда
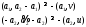
Сложим
последние два неравенства
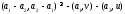 .
.
Следовательно,
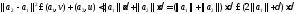 .
Итак, получим, что
.
Итак, получим, что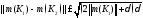 .
Лемма доказана.
.
Лемма доказана.
4.1.3. Теорема.
Отображение
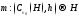 является
непрерывным отображением.
является
непрерывным отображением.
Доказательство.
Докажем,
что для любого открытого множества Vв Н его прообраз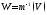 является
открытым множеством. Это означает, что
какое бы
является
открытым множеством. Это означает, что
какое бы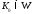 мы
не взяли – существует число
мы
не взяли – существует число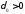 такое, что
такое, что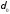 -окрестность
-окрестность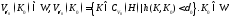 тогда
и только тогда, когда
тогда
и только тогда, когда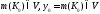 .
Так какV– открытое
множество, то существует число
.
Так какV– открытое
множество, то существует число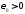 такое, что
такое, что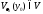 .
Выберем
.
Выберем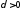 так,
чтобы выполнялось неравенство:
так,
чтобы выполнялось неравенство: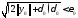 .
Тогда для любого множества
.
Тогда для любого множества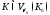 выполнено
выполнено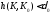 .
В силу леммы 4.1.1
.
В силу леммы 4.1.1 ,
то есть для любого
,
то есть для любого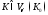 выполняется
включение
выполняется
включение .
Итак, для любого
.
Итак, для любого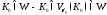 ,
а следовательно, множествоWоткрыто. Теорема доказана.
,
а следовательно, множествоWоткрыто. Теорема доказана.
4.1.4 Следствие.
Пусть X– метрическое пространство, Н –
гильбертово пространство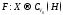 -непрерывное
по Хаусдорфу многозначное отображение.
Тогда для любых
-непрерывное
по Хаусдорфу многозначное отображение.
Тогда для любых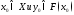
Существует
непрерывное сечение
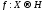 такое,
что
такое,
что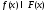 для
любого
для
любого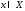 и
выполняется равенство
и
выполняется равенство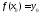 .
.
Доказательство.
Возьмем два случая:
1)Пусть
 ,
тогда возьмем непрерывное отображение
,
тогда возьмем непрерывное отображение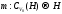 такое,
что для любого
такое,
что для любого
 .
Рассмотрим композицию
.
Рассмотрим композицию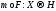 .
Это отображение удовлетворяет условию
.
Это отображение удовлетворяет условию
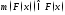 .
Однозначное отображение
.
Однозначное отображение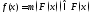 для любого
для любого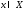 является
сечением многозначного отображенияF.
Отображениеfнепрерывно,
так как является композицией двух
непрерывных однозначных отображений.
Если
является
сечением многозначного отображенияF.
Отображениеfнепрерывно,
так как является композицией двух
непрерывных однозначных отображений.
Если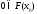 ,
то
,
то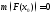 ,то
есть мы построили однозначное отображение
,то
есть мы построили однозначное отображение
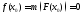 .
.
2)Пусть
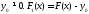 -
непрерывное по Хаусдорфу многозначное
отображение, причем
-
непрерывное по Хаусдорфу многозначное
отображение, причем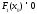 .
Тогда в силу первого случая существует
непрерывное отображение
.
Тогда в силу первого случая существует
непрерывное отображение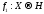 такое,
что
такое,
что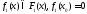 .
Рассмотрим
.
Рассмотрим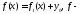 непрерывное,
непрерывное,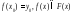
для любого
х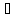 Х.
Следствие доказано.
Х.
Следствие доказано.
