– Разрез

Пропускной способностью (величиной) разреза называется

Сам разрез , называется – разрезом, если .

– разрез называется минимальным, если его пропускная способность меньше любого – разреза

Теорема: пусть множество вершин , тогда для любого потока 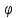справедливо:

Доказательство: докажем, что величина потока для любого разреза есть

Рассмотрим тогда справедливо условие:

Включим , прибавка только в первую сумму на величину потока:

Если начальная и конечная вершина дуги графа принадлежит множеству , то потоки по этим дугам учитываются в первой и второй суммах, и поэтому взаимно уничтожаются, откуда и следует искомое соотношение:

Следствие:

1. Теорема Форда Фалкерсона: Если для некоторого потока и разреза выполняется равенство: , то , .

2. Если для некоторого потока и – разреза выполняется все дуги, входящие в этот разрез должны быть насыщенными, и наоборот.

Доказательство: 1) пусть - максимальный поток, - величина данного потока, необходимо найти разрез равный . Докажем, что существует такой разрез: .

Строим множество :

1)разрез должен быть – разрезом, поэтому

2)если вершина попала в

2а) и есть дуга , по которой , то тогда

2б) и причём , то .

Покажем, что разрез является – разрезом:

по условию, покажем, что .

Предположим противное: пусть попала в , тогда существует путь (цепь) из в , все вершины которого лежат в , тогда рассмотрим 2 соседние вершины (все пары) и 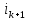. Для всех дуг, соединяющие эти вершины, посчитаем:

Теперь в качестве и построим другой поток.

Поток по каждой прямой дуге, попавшей по причине 2а увеличим на , по причине 2б – уменьшим на .

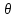Тогда мы построим новый поток, условие баланса не нарушено:

Получено противоречие.

Покажем, что величина разреза совпадает с величиной потока. Рассмотрим дуги - лежащие в разрезе: 1), если согласно 2а - противоречие. – насыщенная.

2), , Согласно 2б - противоречие, для всех вершин.

по теореме