Метрические характеристики графа.

– связный неориентированный граф.

Расстояние – длина кратчайшего маршрута. Введенное таким образом расстояние

1. 

2. 

3. 

Если можно ввести матрицу расстояний

Эксцентриситет вершины это максимальное из расстояний из вершины до всех других вершин.

Диаметр графа - это максимальный из всех эксцентриситетов.

Радиус графа - это минимальный из всех эксцентриситетов.

Вершина называется периферийной, если её эксцентриситет совпадает с диаметром.

Вершина называется центральной, если её эксцентриситет совпадает с радиусом.

Взвешенные графы.

Пусть – вес дуги . Если есть маршрут связывающий , то тогда длина этого маршрута , Тогда взвешенным расстоянием между вершинами и – это минимум из длин

Эксцентриситет – максимальное из всех взвешенных расстояний

взвешенной центральной вершиной, если её эксцентриситет минимальный из всех возможных:

Нахождение кратчайшего пути.

– взвешенный ориентированный граф.

Рассмотрим вершины и (есть хотя бы один путь).

Алгоритм Дейкстра нахождения кратчайшего пути.

Этап 1. Нахождение длины кратчайшего пути.

ШАГ 1.Присвоение начальных меток:

- текущая вершина.

ШАГ 2.Изменение меток: для всех вершин , непосредственно следующих за вершиной 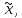с временными метками, меняем метки в соответствие со следующим правилом:

ШАГ 3.Превращение меток из временной в постоянную: из всех вершин с временными метками выбираем

( – временная, - постоянная)

ШАГ 4.Проверка на завершение первого этапа.

Если , то – длина кратчайшего пути, иначе переход к шагу 2.

Этап 2. Построение кратчайшего пути.

Среди вершин непосредственно предшествующих вершине находим такую , что . Дугу включаем в кратчайший маршрут. После , до тех пор, пока .

Определения:

Дерево - связный неориентированный граф, не содержащий циклов.

Лес – циклический неориентированный граф.

Ориентированный граф называется ориентированным деревом, если существует ровно одна вершина, корень, не имеющая предшественников, и любой вершине, отличной от корня, предшествует ровно ода вершина.

Основные числа теории графов.

1. Хроматическое число графа. – неориентированный граф без петель. Граф называется правильно раскрашенным, если каждой его вершине приписан какой-либо цвет, а две соседние вершины окрашены в разные цвета. Минимальное число цветов, в которое может быть окрашен правильно раскрашенный граф, называется хроматическим числом графа . Если , тогда называют хроматическим. Теорема: для того, чтобы связный неориентированный граф без петель являлся бихроматическим необходимо и достаточно, чтобы он не содержал простых циклов нечетной длины. Доказательство: I Необходимость Пусть – бихроматический. Предположим противное: пусть в нем содержится простой цикл нечётной длины Получено противоречие. II Достаточность Пусть не содержит простых циклов нечетной длины Удаляем ребра в циклах так, чтобы удалить циклы и граф стал деревом - бихроматический В силу четности циклов вершины, которые соединяют удалённые ребра, буду окрашены в разные цвета. И поэтому правильная раскраска графа не нарушится. ч.т.д. Рассмотрим некоторую вершину 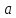. Через обозначим степень вершины, то есть число инцидентных ей ребер (если при это вершина содержит петлю, то считаем её дважды). Если стеки всех вершин графа чётные, то граф называют чётным. Через 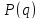обозначим наибольшую из степеней вершин графа. Тогда справедлива Теорема: Для любого неориентированного графа справедлива следующая оценка: . Определение: плоским называется граф, вершины которого являются точками плоскости, а ребра – непрерывными плоскими линиями без самопересечения, такими, что никакие 2 ребра не имеют общих точек, кроме инцидентных или общих вершин. Любой граф изоморфный плоскому называют планарным графом. Гипотеза: всякий планарный граф можно раскрасить не более чем 4 красками. Если окрашены уже вершины , то новые произвольно взятые вершины мы приписываем минимальный из цветов, в который не окрашены соседние с ней вершины.

2. Число внутренней и внешней устойчивости. - ориентированный граф. Рассмотрим Подмножество вершин J называется внутренне устойчивым, если J , то есть множество J не содержит соседние вершины. Числом внутренней устойчивости графа называется J - максимальная мощность внутренней устойчивости Подмножество E вершин графа называется внешне устойчивым множеством, если E

3. Цикломатическое число графа - число дуг, – число вершин, - число компонентов связности

Транспортные сети.

Говорят, что задана транспортная сеть, если заданы 2 объекта:

• Ориентированный связный граф , обладающий следующими свойствами

  • не содержит циклов

  • - источник, не имеющая предшественников,

  • – сток, не имеющая последователей,

• Функция , действующая из множества дуг в расширенный натуральный ряд,, - пропускная способность дуги.

– множество дуг, входящих в

– множество дуг, исходящих из

Функция , называется потоком, если

• 

• справедливо условие баланса

• 

Тогда величина

- величина потока

Поток называется максимальным, если его величина .

Величина - остаточная пропускная способность дуги , если , дуга называется насыщенной; а поток , из которого каждый путь, идущий из в содержит хотя бы одну насыщенную дугу называется полным потоком.

Рассмотрим некоторое подмножество вершин графа .

Множество дуг, начало которых лежит в множестве , а концы в множестве , называется ориентированным разрезом: