Элементы теории алгоритмов.

Машина Тьюринга – это воображаемая машина:

1. Бесконечная лента, которая поделена на ячейки, в которых находятся символы

2. Внешний алфавит: совокупность знаков, с помощью которых записываются слова , - пустой символ

3. Устройство управления, может останавливаться на месте или двигаться влево, вправо

4. Внутренний алфавит – совокупность состояний машины , – особое «стоп» состояние, – начальное

При работе над словом возможны 2 ситуации:

• После конечного числа шагов машина останавливается (переход в состояние ) и на ленте оказывается изображенным некоторое слово, в этом случае говорят, что машина применима к начальному слову и преобразовывает его в другое слово;

• Машина никогда не останавливается (есть , но она к нему не переходит), в этом случае говорят, что машина не применима к данному слову.

Пусть на некотором шаге машина в состоянии устройство управления находится над ; мы должны заменить его на , устройство управления должны оставить на месте или сместить:

Совокупность таких команд называется программой машины Тьюринга.

Тьюринговая функциональная система

Вычисление по Тьюрингу функций.

Рассмотрим расширенный натуральный ряд: , рассмотрим функции от переменных , где

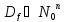
Такие функции называются частичными функциями счётнозначной логики. Множество функций .

Если область определения функции совпадает со всем , то тогда 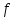называется всюду определенной.

Пусть , 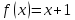; закодируем числа натурального ряда: , тогда слово будем записывать на ленте

Определение: говорят, что функция вычислима по Тьюрингу, если существует машина Тьюринга, работающая в алфавите и обладающая следующими свойствами:

1. Если набор - область определения и , то машина Тьюринга применима к слову в начальной конфигурации

2. Если , то машина не применима к слову в начальной конфигурации, то есть начиная работу над словом она начинает циклить.

Рекурсивные функции:

1. 0 – функция:

2. Функция следования

3. Оператор проектирования

Введем следующие операции:

1. Операция суперпозиции: …

2. Примитивная рекурсия

3. Процедура взятия оператора Ищем следующим образом:

Определение: функция называется частично рекурсивной, если она может быть получена из простейших функций: 0 – функции, функции следования, функции выбора переменной, с помощью конечного числа применений суперпозиций примитивной рекурсии и взятия оператора. Если функция всюду определена и частична рекурсивна, она называется общерекурсивной функцией.

Теорема: всякая частично рекурсивная функция вычислима по Тьюрингу и наоборот: всякая вычислимая по Тьюрингу функция является частично рекурсивной.

Определение: множество называется общерекурсивным, если оно совпадает с множеством значений некоторой общерекурсивной функции (например множество чётных чисел).

Определение: рассмотрим некоторое множество , которое является подмножеством некоторого множества, тогда характеристической функцией данного множества

Определение: множество называется рекурсивным, если его характеристическая функция частично рекурсивная.

Теорема: всякое рекурсивное множество является общерекурсивным. Нормальные алгоритмы Маркова.

Рассмотрим некоторую совокупность символов – алфавит , - слово, – пустое слово. Определение: Марковской подстановкой называется операция, которая записывается , которая ищет первое вхождение слова в некоторое слово и заменяет слово на слово . – если дальше продолжаем работу

– окончание работы после

Работа алгоритма происходит следующим образом: рассматривается слово и ищется первое , если ни одно из не является подсловом , то в этом случае алгоритм не начинает свою работу, иначе и получаем новое слово . Если эта подстановка была заключительной, то останавливаемся и результат , иначе начинаем работу сначала, но уже с .

Определение: функция, заданная на некотором множестве слов алфавита называется нормально вычислимой, если существует такое расширение данного алфавита и такой нормальный алгоритм Маркова, работающий над словами алфавита , который каждое слово из области определения функции преобразует слово в , такое, что .

Принципы нормализации алгоритма Маркова:

Для нахождения значений функции в некотором алфавите тогда и только тогда существует алгоритм, когда функция нормально вычислима.

Теорема: следующие классы функций (заданы на расширенном натуральном ряде и принимают значения с расширенного натурального ряда) совпадают:

1. Класс функций, вычислимых по Тьюрингу

2. Класс частично рекурсивных функций

3. Класс нормально вычислимых функций

Неразрешимые алгоритмические проблемы:

1. Проблема распознавания выводимости в математической логике: для любых двух формул и в логическом исчислении узнать, существует ли дедуктивная цепочка, ведущая от формулы к формуле Теорема Чёрча: проблема распознавания выводимости алгоритмически не разрешима.

2. Проблема распознавания самоприменимости. – код символа. - код команды. Тогда наша программа – совокупность команд На вход машины Тьюринга Т отправляем 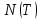1) если машина Тьюринга применима к своему коду – самопримаенимая 2) если начиная работу над своим кодом машина Тьюринга циклит – несамоприменимая Таким образом все машины Тьюринга, работающие в алфавите делятся на 2 класса: самоприменимые и несамоприменимые. Проблема самоприменимости состоит в следующем: построить такой алгоритм, который по коду машины Тьюринга Т давал бы однозначный ответ самоприменима машина Т или нет (без запуска). Для решения проблемы необходимо построить машину в алфавите , которая, работая над кодом машины Тьюринга Т, останавливалась и выдавала 1, самоприменима, или 0. Теорема: проблема самоприменимости алгоритмически не разрешена. Доказательство: предположим противное: пусть существует машина , решающая проблему самоприменимости. Опираясь на неё, построим машину Тьюринга , которая: 1) применима к кодам несамоприменимых машин Тьюринга, 2) не применима к кодам самоприменимых машин Тьюринга. Для этого: 1) все команды машины объявляем командами машины ; 2) заключительное состояние 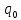машины объявляем не заключительным для машины ; 3) добавляем заключительное состояние для и команды: Машина работает над кодами всех машин, в том числе и на своим. Пусть 1) машина Тьюринга самоприменима, то есть применима к своему коду, но она не применима к кодам самоприменимых машин, значит является несамоприменимой. Получено противоречие. 2) машина Тьюринга несамоприменима, но она применима к кодам несамоприменимых машин, значит самоприменима. Получено противоречие.

3. Проблема применимости. Машина Тьюринга работает в алфавите , - слово. Требуется по коду машины Тьюринга Т и слову определить, применима ли машина Тьюринга к слову или нет. В разработке такого алгоритма и заключается проблема применимости: построить машину Тьюринга , на вход которой поступает . В результате 1, если машина применима, иначе 0. Теорема: проблема применимости алгоритмически неразрешима. Доказательство: предположим противное: пусть машину Тьюринга можно построить, тогда наш код - это машина . Подадим слово , тогда машина решала бы проблему самоприменимости, а она алгоритмически неразрешима.

4. Проблема определения общей рекурсивности алгоримов, т.е. проблема определения того, ко всяким ли допустимым в начале данным применим данный алгоритм. алгоритм. Нужно построить , на вход которой бы поступал номер алгоритма . В результате: 1 – алгоритм всюду определён, 0 – алгоритм не является общим. Лемма: для любого перечисления любого множества 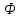общерекурсивных функций существует функция, не входящая в это перечисление. Доказательство: рассмотрим все общерекурсивные функции и функцию 𝐹 общерекурсивная. Будем предполагать, что , тогда в нашем перечислении имеет номер , тогда совпадает с , но . Получено противоречие. Теорема: проблема определения общерекурсивных функций алгоритмически неразрешима. Доказательство: предположим противное: пусть алгоритм , решающий проблему, существует, тогда он определяет общерекурсивную функцию . На основании построим общерекурсивную функцию следующего вида: Построенная функция 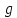перечисляет все общерекурсивные функции, а так как множество общерекурсивных функций не является счётным, то получили противоречие.

Теория графов.

Основные понятия и определения.

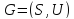Графом называется пара , , где - это множество вершин (в начальном варианте считается конечным и непустым), - бинарное отношение, заданное на , - множество дуг. Элементы множества - упорядоченные пары – дуги, где - начало, - конец.

Вершины, соединённые дугой, называют инцидентными дуге. Между собой – смежными (соединенными одной дугой).

Дуги, имеющие общую вершину, - смежные.

Граф называется ориентированным (орграфом), если Если в этом случае граф называют неориентированным (неоргаф).

- ребро, без направления.

Если необходимо представить объекты, связанные несколькими связями, используют мультиграф.

Граф, не содержащий кратных дуг и петель называется простым графом.

Если дугам или вершинам необходимо приписать числа, то речь идёт о взвешенном графе.

Для взвешенного графа : - функция распределения меток вершин, - множество значений; - функция распределения меток дуг, - множество значений.

Простой граф, в котором каждая пара вершин является смежной, называется полным графом.

Пусть , если , то тогда это множество подмножеств называется покрытием .

Граф называется двудольным, если существует такое разбиение множества вершин на два подмножества (доли), что концы каждого ребра принадлежат разным подмножествам (долям), если при этом любые две вершины, входящие в разные дуги, являются смежными, то граф называется полным двудольным графом.

Полный двудольный граф, содержащий в одной доле один элемент – звезда.

Рассмотрим графы ,.

Графы называются гомоморфными, если существует отображение (гомоморфизмом) со свойством:

Если , то - изоморфизм, а графы и изоморфные.

Способы задания графов.

1. Графически

2. Матрица смежности. , ; матрицей смежности называется матрица 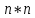, в которой элемент Для мультиграфов: , - число дуг, связывающих и Для взвешенных графов Рангом графа называется ранг его матрицы смежности. Собственным значением графа называется собственное значение матрицы смежности. Спектром графа называется спектр его матрицы смежности.

3. Матрица инцидентности Строим матрицу инцидентности

4. Структура смежности Для дуги 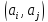: 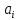– предшественник (предок), – последователь (потомок). Выписываем вершины и их прямых последователей.

Подграфы. Операции над графами.

Определение: граф называется подграфом графа , если

Операции над графами:

1. Добавление вершины

2. Добавление дуги

3. Удаление дуги

4. Удаление вершины

5. Отождествление вершин Если и были связаны дугой, то операция отождествления называется операцией стягивания вершины.

6. Объединение графов и

7. Пересечение графов и

8. Кольцевая сумма графов и

Маршруты. Цепи. Циклы.

Последовательность вершин и соединяющих их дуг называется маршрутом из в .

Число дуг называется длиной маршрута.

Пусть неориентированный граф (без петель).

Маршрут называется цепью, если все его ребра различны.

Простой цепью, если при этом все его вершины (кроме, возможно, первой и последней) различны.

Маршрут называется циклическим, если совпадает с .

Циклическая цепь называется циклом. Циклическая простая цепь – простым циклом.

Замечание: для ориентированного графа вводится понятие ориентированного маршрута. Аналогом цепи в этом случае служит путь. Аналогом цикла – контур.

Утверждения:

• При всякий маршрут, соединяющий эти вершины, содержит простую цепь, соединяющую эти вершины.

• Всякий цикл содержит простой цикл

• Объединение двух несовпадающих простых цепей, соединяющих и , содержит простой цикл.

• Пусть и два несовпадающих простых цикла, имеющих общее ребро , тогда граф , получаемый путем объединения и и удаления дуги , содержит так же простой цикл. и - подцепи, - цепь, по предыдущему утверждению.

• Две вершины и неориентированного графа называются связными, если существует маршрут ( цепь) из ребер графа, в котором одна из этих вершин является началом, вторая – концом. Таким образом на множестве вершин графа можно ввести бинарное отношение , такое, что пара вершин и связны. Данное отношение является отношением эквивалентности. И позволяет разбить множество на непересекающиеся классы эквивалентности 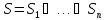,каждый из которых называется множеством связности. В этом случае подграф 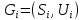, где - все дуги исходного графа, связывающие вершины , называется компонентой связного графа.

Граф называется связным, если он содержит ровно одну компоненту связности.