Понятие равносильной формулы.
Формула логики предикатов называется общезначимой или тавтологией, если при всякой подстановке вместо её предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах она превращается в тождественно истинный предикат.
Формулы
и
называются равносильными на множестве
если при любой замене имеющихся в них
простых (элементарных) формул на
предикаты, заданные на множестве
,
данные формулы превращаются в равносильные
предикаты.
Формулы
и
называются равносильными, если они
равносильны на любых множествах.
Основные равносильные предикаты:
Пусть
и
– переменные предикаты, в которые
переменная
входит свободно,
- некоторое высказывание, тогда
справедливо:
Приведенная форма для формулы предикатов.
Формула
равносильная данной и не содержащая
других операций логики высказывания,
кроме
,
в которой отрицание относится только
к простым формулам, называется формулой
приведенной формы. (нормальной)
Теорема: для любой формулы логики предикатов существует равносильная ей приведенная формула.
Доказательство:
(методом математической индукции по
числу логических связок). Пусть
- число логических связок.
Пусть
,
тогда формула не имеет логических
связок.
Пусть
при
формула верна. Докажем для
.
Разобьем
произвольно на 2 части, в каждой из
которых меньше, чем
логических связок.
Тогда
по предположению для
и
можем построить приведенные формы
и
,
тогда,
-
Если
,
то
-
Если
,
то
-
Если
,
то если
является простой, то
составная, тогда для
мы должны перенести отрицания с помощью
законов де Моргана;
-
Если
,
то
Предваренная нормальная форма для формул логики предикатов.
Определение:
говорят, что предикатная формула
записана в предваренной нормальной
форме, если она имеет следующий вид:
,
где
,
- переменная, связанная с квантором
,
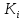- формула в приведенной форме и не
содержит кванторов.
Теорема: для любой формулы логики предикатов существует равносильная ей предваренная форма.
Доказательство: методом математической индукции по числу логических и кванторных операций.
- формула
логики предикатов
Если
0 – число логических и кванторных
операций, тогда
- простая,
- предваренная,
.
Предполагаем
истинность для
операций.
Докажем
истинность при
.
Выделим в
2 части:
или
Все
формулы
и
содержит
операцию, поэтому, по предположению,
для них есть предваренные формы
и
-
Если
;
если в
есть кванторы, то необходимо ввести
отрицание под элементарные формулы и
заменить кванторы
Если
отрицание относится к составной
формуле, используем законы де Моргана.
-
тогда у нас есть
предваренная форма для
-
;
рассмотрим предваренные формы для
и
и переобозначим связные переменные
так, чтобы все они были различны:
