Классификация предикатов:

Предикат называется тождественно истинным на множестве , если любая её конкретизация является истинным высказыванием.

Предикат 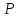называется выполнимым на множестве 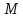, если существует набор предметных констант, на котором предикат превращается в истинное высказывание.

Предикат называется опровержимым на множестве , если существует набор предметных констант, на котором предикат превращается в ложное высказывание.

Предикат называется тождественно ложным на множестве , если любая её конкретизация является ложным высказыванием.

Два местных предиката и заданных на одних и тех же множествах называются равносильными, , если они принимают одинаковые значения на одних и тех же наборах переменных. Или другими словами .

Предикат заданный на множествах называется логическим следствием предиката заданного на тех же множествах, , если он превращается в истинное высказывание на тех же наборах переменных, на которых превращается в истинное высказывание предикат .

Операции над предикатами:

1. Отрицание предиката Отрицанием местного предиката , заданного на множестве , называется местный предикат , такой, что

2. Конъюнкция предикатов Конъюнкцией предикатов и называется новый предикат

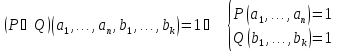
3. Дизъюнкция предикатов Дизъюнкцией двух предикатов 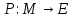и называется новый предикат

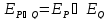
4. Импликация предикатов Импликацией двух предикатов 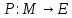и называется новый предикат

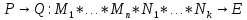
Операции, связанные кванторами.

Рассмотрим одноместный предикат .

Операциями, связанными кванторами общности, называются правила, по которым одноместному предикату ставится в соответствие высказывание 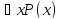(для всех/любого):

Операциями, связанными кванторами существования, называются правила, по которым одноместному предикату ставится в соответствие высказывание : .

Теорема: пусть одноместный предикат и , тогда и .

Доказательство: Пусть ;

Пусть

Операция, связывания квантора общности предиката по переменной называется правило, по которому местному предикату ставится в соответствие местный предикат который для каждого набора предметных постоянных превращается в высказывание которое истинно одноместный предикат является тождественно истинным на множестве .

Формулы логики предикатов.

Алфавит символов:

1. Предметные переменные

2. 0-местные предикаты (высказывания)

3. местные предикатные переменные

4. Символы операций:

5. Кванторы

6. Скобки

Определение:

1. Каждая 0-местная предикатная переменная является формулой

2. Если местная предикатная переменная, то - формула, в которой предметные переменные – свободные

3. Если 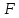- формула, то так же является формулой, в которой свободные те же переменные, которые свободные и в , и связаны те переменные, которые и были связанны.

4. Если и - формулы, то выражения так же являются формулами, причём: те переменные, которые свободны хотя бы в одной из формул объявляются свободными в новых формулах, а те переменные, которые связны хотя бы в одной из формул являются связными и в новой формуле.

5. Если - формула, в которой переменная входит свободно, то и так же являются формулами, в которой переменная является связной.

6. Никаких других формул в логике предикатов нет.

Формулы, в которых нет свободных переменных, называются замкнутыми.

Формулы, содержащие свободные переменные называются открытыми.

Логические значения формулы логики предикатов зависит от значений трёх видов переменных:

1. Значений, входящих в формулу переменных высказывания

2. Значений, свободных предметных переменных

3. Значений, предикатных переменных, входящих в формулу.