
- •Глава 1. Финансовые ренты
- •§1. Классификация рент
- •§2 . Финансовый анализ базовых рент пренумерандо и постнумерандо
- •2.1.Коэффициенты дисконтирования и наращения рент
- •2.2. Свойства коэффициентов дисконтирования и наращения рент
- •§3. Oтсроченные m-кратные ренты и непрерывные ренты
- •3.1. Отсроченные ренты
- •3.2. M-кратные ренты
- •3.3 Непрерывные ренты
- •Глава 2. Сравнительный финансовый анализ инвестиционных и других коммерческих проектов
- •§1. Модели потока платежей 1.1 Модель дискретного потока платежей
- •1.2 Модель непрерывного потока платежей
- •1.3 Модель непрерывно-дискретного потока платежей
- •1.4 Еще о связи коэффициентов наращения и дисконтирования
- •1.5 Уравнивающее время для серии долговых платежей
- •§2. Внутренняя норма доходности инвестиционного проекта
- •2.1 Вывод основного уравнения
- •§ 3. Срок окупаемости капиталовложений и индекс рентабельности инвестиционного проекта
- •3.1 Срок окупаемости капиталовложений
- •§4. Индекс рентабельности
- •Некоторые общие замечания о методике выбора инвестиционного проекта
- •Глава 3. Индексы инфляции и неравенства в распределении семейных доходов
- •§1. Учет и инфляции
- •Индекс и темпы роста инфляции
- •Индексация ставки процента
- •Учет инфляции в инвестиционных проектах
- •§2 Индекс неравенства в распределении семейных доходов
- •2.1 Кривая Лоренца
- •2.2 Коэффициент Джини
1.4 Еще о связи коэффициентов наращения и дисконтирования
Если
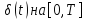 – неотрицательная переменная интенсивность
процента за базовую единицу времени ,
начинающуюся в моментt,
то при
– неотрицательная переменная интенсивность
процента за базовую единицу времени ,
начинающуюся в моментt,
то при
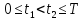
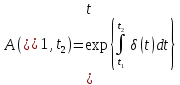 (2.9)
(2.9)
- коэффициент наращения одной денежной единицы на интервале (t1, t2) при движении по нему слева направо, а
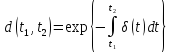 (2.10)
(2.10)
-
коэффициент дисконтирования одной
денежной единицы с момента t2
на момент t1
т.е.
при движении по интервалу (t1
,
t2)
справа налево. Из курса математического
анализа известно, что при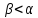
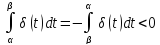 .
(2.11)
.
(2.11)
Поэтому (14,12)-(14,13) при t1<t2 влекут за собой следующие равенства:
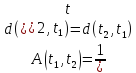 ,
(2.12)
,
(2.12)
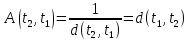 .
(2.13)
.
(2.13)
Если же t1>t2 коэффициент дисконтирования d(t1, t2) играет роль коэффициента наращения A(t2, t1) и в силу (15,13) и (15,14) совпадает с ним. Поэтому формулы (2.12)-(2.13) и (2.15)-(2.16) справедливы ,как при t1<t2, так и при t1>t2.
Заметим теперь, что поскольку в рассматриваемом случае
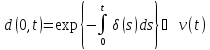 ,
,
и всегда
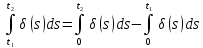 ,
,
то (15,12), (15,13) при любых t1 и t2 можно записать в виде
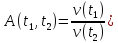 ,
,
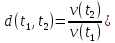 .
(2.17)
.
(2.17)
Отсюда также следует справедливость (2.15), (2.16).
Таким образом, коэффициенты наращения и дисконтирования взаимозаменяемы и с математической точки зрения можно было бы пользоваться только одним из них. Однако, в интересах наглядности принято пользоваться двумя коэффициентами.
1.5 Уравнивающее время для серии долговых платежей
Должник
обязался погасить свой долг последовательными
платежами величиной x1,
x2,
…, xn
в моменты соответственно t1,
t2,
…, tn.
Следовательно, речь идет одностороннем
потоке платежей
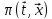 .
Обозначим сумму всех недисконтированных
платежей через
.
Обозначим сумму всех недисконтированных
платежей через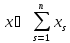 ,
а весs-го
платежа – через
,
а весs-го
платежа – через
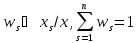 .
.
Должник предлагает кредитору погасить свою задолженность одним платежом суммы x в момент
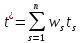 (2.18)
(2.18)
который
является взвешенным среднем арифметическим
для моментов всех выплат. Поскольку в
(2.18) не входит процентная ставка, то
кредитор предлагает должнику произвести
платеж x
в момент T,
определяемый из условия эквивалентности
потоков платежей
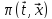 и
и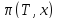 при известном
при известном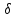 :
:
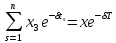 .
(2.19)
.
(2.19)
Поделив обе части этого уравнения на x, найдем из него T в виде
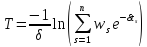 .
(2.20)
.
(2.20)
Величина
T
называется уравнивающим временем для
данного потока платежей при фиксированном
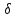 .
.
Теорема
2.1
Если
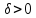 ,
то
,
то
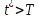 ,
(2.21)
,
(2.21)
т.е.
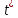 выгоднее для должника, аT
– для кредитора.
выгоднее для должника, аT
– для кредитора.
Заметим,
что так как
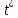 не зависит от
не зависит от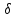 ,
то
,
то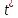 можно использовать как приближенную
оценку дляT,
погрешность которой зависит от
можно использовать как приближенную
оценку дляT,
погрешность которой зависит от
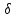 .
.
§2. Внутренняя норма доходности инвестиционного проекта
2.1 Вывод основного уравнения
Экономический анализ эффективности планируемых среднесрочных и особенно долгосрочных инвестиций является сложной задачей. Для выбора наилучших объектов и вариантов вложения средств во всем мире применяются несколько методик. Чаще всего они основаны на использовании следующих четырех показателей для сравнения вариантов инвестиций:
Чистая текущая стоимость
Внутренняя норма доходности
Период окупаемости
Индекс рентабельности
Первым
показателем является рассмотренная в
предыдущем параграфе чистая текущая
стоимость проекта, совпадающая с NPV
порождаемого проектом потока платежей.
Действительно, отрицательное значение
NPV
говорит о нецелесообразности для
инвестора рассматриваемого варианта
потока платежей
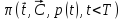 при данном наборе значений
при данном наборе значений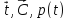 и эффективной годовой ставке
и эффективной годовой ставке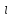 .
Среди вариантов с положительнымNPV
π естественно выбрать тот, у кого NPV
π больше. Однако этот лучший по NPV
π
вариант надо еще сравнить с вариантом
вложения средств на банковский депозит,
что может оказаться более рентабельным
и к тому же менее рискованным.
.
Среди вариантов с положительнымNPV
π естественно выбрать тот, у кого NPV
π больше. Однако этот лучший по NPV
π
вариант надо еще сравнить с вариантом
вложения средств на банковский депозит,
что может оказаться более рентабельным
и к тому же менее рискованным.
Для этой цели служит второй показатель – внутренняя норма доходности (Internal Rate of Return = IRR)
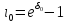 ,
(2.22)
,
(2.22)
где
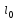 является корнем уравнения
является корнем уравнения
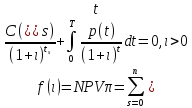 (2.23)
(2.23)
Это уравнение называется уравнением стоимости или уравнением доходности для проекта на момент 0.
Смысл
уравнения (2.23) состоит в том, что
приведенные на тот момент
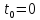 начала проекта значения потоков расходов
и доходов совпадают, т.е. проект является
бесприбыльным.
начала проекта значения потоков расходов
и доходов совпадают, т.е. проект является
бесприбыльным.
Определение
Если уравнения
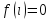 существует единственный платежный
кореньi0,
то его называют ставкой доходности
проекта или внутренней нормой доходности
(IRR)
за базовую единицу времени.
существует единственный платежный
кореньi0,
то его называют ставкой доходности
проекта или внутренней нормой доходности
(IRR)
за базовую единицу времени.
Если
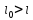 ,
где
,
где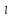 - эффективная рыночная ставка процента,
то соответствующий проект нужно
отвергнуть, а если
- эффективная рыночная ставка процента,
то соответствующий проект нужно
отвергнуть, а если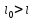 - соответствующий проект, в принципе,
можно принять выбрав из всех вариантов
проект с наибольшим значением
- соответствующий проект, в принципе,
можно принять выбрав из всех вариантов
проект с наибольшим значением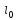 .
Таким образом, экономическая задача
требует решения чисто математической
задачи – отыскания корней уравнения
(2.23).
.
Таким образом, экономическая задача
требует решения чисто математической
задачи – отыскания корней уравнения
(2.23).
Очевидно, что если поток π платежей задан, то
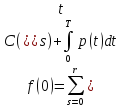 (2.24)
(2.24)
- недисконтированная сумма всех нетто-платежей за срок проекта. При этом из финансового смысла следует, что нужно отвергнуть все варианты с f(0)<0 и рассматривать лишь варианты, для которых
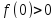 .
(2.25)
.
(2.25)
Далее при очень больших значениях i имеем:
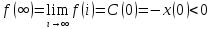 ,
(2.26)
,
(2.26)
Где С(0) – начальная инвестиция.
Теорема
2.2.
Если все отрицательные платежи
предшествуют всем положительным и
наоборот, то
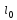 определено.
определено.
Теорема
2.3
(обобщает
предыдущую). Пусть
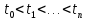 и
и
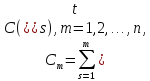 (2.27)
(2.27)
- накопленная сумма всех нетто-платежей инвестора от момента 0 до момента tm включительно.
Если
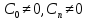 и если после исключения нулевых значений
последовательность (C0,
C1,
…, Cn)
имеет ровно одну перемену знака, то
уравнение доходности (2.23) имеет
единственный положительный корень,
т.е.
и если после исключения нулевых значений
последовательность (C0,
C1,
…, Cn)
имеет ровно одну перемену знака, то
уравнение доходности (2.23) имеет
единственный положительный корень,
т.е.
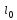 определено.
определено.
