
- •Список вопросов к экзамену по математическому анализу
- •2. Критерий Коши сходимости знакопостоянного ряда.
- •3. Признаки сравнения знакопостоянных рядов.
- •4. Знакопеременные ряды. Абсолютная и условная сходимость ряда.
- •5. Признаки Лейбница, Абеля и Дирихле сходимости знакопеременных рядов.
- •6. Действия над рядами. Сумма и произведение рядов.
- •7. Функциональные ряды. Область сходимости функционального ряда.
- •8. Равномерная сходимость. Мажорантный признак Вейерштрасса.
- •9. Степенные ряды. Интервал и радиус сходимости. Ряд Тейлора.
- •10. Ряд Фурье. Условие поточечной сходимости.
- •11.Ряд Фурье. Условие равномерной сходимости.
- •12.Представление функции в виде интеграла Фурье
- •13. Преобразование Фурье
- •14. Собственные интегралы, зависящие от параметра. Предельный переход под знаком интеграла.
- •15.Дифференцирование и интегрирование под знаком интеграла
- •16. Г- и в- функции Эйлера и их основные свойства.
- •17.Двойной интеграл. Теорема о среднем.
- •18. Сведение двойного интеграла к повторному.
- •19. Приложения двойного интеграла.
- •20. Замена переменных в двойном интеграле.
- •21.Тройной интеграл. Приложения тройного интеграла.
- •22.Сведение тройного интеграла к повторному.
- •23.Замена переменных в тройном интеграле.
- •24.Криволинейные интегралы первого и второго рода.
- •25.Теорема Грина.
- •26.Поверхностные интегралы первого и второго рода.
- •27.Теоремы Остроградского-Гаусса и Стокса.
- •28.Элементы теории поля. Дифференциальные векторные операции.
24.Криволинейные интегралы первого и второго рода.
Зададим кривую f(x,y).
Разобьем кривую наnотрезков и выберем на каждом из них
произвольную точку .
Обозначим
.
Обозначим -
наибольший из диаметров всех отрезков
-
наибольший из диаметров всех отрезков .
Тогда, интегральная сумма равна
.
Тогда, интегральная сумма равна ,
где
,
где длина
отрезка
длина
отрезка .
Криволинейным интеграломIрода называется
.
Криволинейным интеграломIрода называется ,
если он существует конечен и не зависит
от диаметра разбиения и длин отрезков.
Еслиf(x,y)-
непрерывная функция,y(x)
— непрерывно дифференцируема на [a,b],
то
,
если он существует конечен и не зависит
от диаметра разбиения и длин отрезков.
Еслиf(x,y)-
непрерывная функция,y(x)
— непрерывно дифференцируема на [a,b],
то .
Для случая параметрически заданной
кривой:
.
Для случая параметрически заданной
кривой: .
.
Криволинейные интегралы второго рода:
Пусть дана непрерывная и
незамкнутая кривая (AB),
вдоль которой задана функцияf(x,y).
Выберем на отрезке кривой произвольную
точку
произвольную
точку ,
вычислим в ней значение функции
,
вычислим в ней значение функции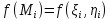 ,
это значение умножим на проекцию дуги
на осьx, т. е. на
,
это значение умножим на проекцию дуги
на осьx, т. е. на ,
составим сумму:
,
составим сумму: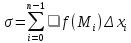 ,
если при стремлении
,
если при стремлении к
нулю эта сумма имеет конечный пределI, не зависящий ни от
способа дробления кривой, ни от выбора
промежуточных точек, то такой предел
называется криволинейным интегралом
отf(M)dx,
взятым по пути (AB),
обозначается
к
нулю эта сумма имеет конечный пределI, не зависящий ни от
способа дробления кривой, ни от выбора
промежуточных точек, то такой предел
называется криволинейным интегралом
отf(M)dx,
взятым по пути (AB),
обозначается ,
аналогично получаем для осиy
,
аналогично получаем для осиy .
Если вдоль кривой (AB)
определены две функцииP(M)=P(x,y),Q(M)=Q(x,y)
и существуют интегралы
.
Если вдоль кривой (AB)
определены две функцииP(M)=P(x,y),Q(M)=Q(x,y)
и существуют интегралы ,
то их сумму называют криволинейным
интегралом общего вида и полагают
,
то их сумму называют криволинейным
интегралом общего вида и полагают .
.
25.Теорема Грина.
Теорема: Пусть ф-ции P,Q, -
непрерывны в областиD, Г
— граница областиD. Тогда
справедлива формула:
-
непрерывны в областиD, Г
— граница областиD. Тогда
справедлива формула: -
формула Грина.
-
формула Грина.
Доказательство:
 ,
, .
Рассмотрим областьD,
ограниченную контуром Г, состоящим из
кривых
.
Рассмотрим областьD,
ограниченную контуром Г, состоящим из
кривых
(PQ):
(SR): ,
вычислим двойной интеграл
,
вычислим двойной интеграл
Видим,
что
 ,
,
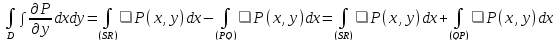 .
Для рассмотрения интеграла по всему
контуру Г областиD,
прибавим к правой части полученного
равенства еще интегралы
.
Для рассмотрения интеграла по всему
контуру Г областиD,
прибавим к правой части полученного
равенства еще интегралы ,
равные нулю, так как отрезки (PS)
и (RQ) перпендикулярны к
осиx, получим,
,
равные нулю, так как отрезки (PS)
и (RQ) перпендикулярны к
осиx, получим, .
Аналогично для
.
Аналогично для .
Таким образом, теорема доказана.
.
Таким образом, теорема доказана.
26.Поверхностные интегралы первого и второго рода.
Первого рода: Пусть в точках
некоторой двусторонней гладкой
поверхности (S), ограниченной
контуром, определена функцияf(M)=f(x,y,z).
Разобьем поверхность (S)
с помощью сети произвольно проведенных
кривых на части, взяв в каждой части по
произволу точку , вычислим в этой точке
значение функции, и, умножив на площадь
соответствующей части пов-ти, составим
интегральную сумму
по
произволу точку , вычислим в этой точке
значение функции, и, умножив на площадь
соответствующей части пов-ти, составим
интегральную сумму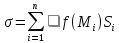 .
Поверхностным интегралом первого рода
называется предел этой суммы при
стремлении диаметров всех частей
поверхноси к нулю, если этот предел
существует, конечен и не зависит от
количества разбиений и выбора промежуточных
точек. Обозначение:
.
Поверхностным интегралом первого рода
называется предел этой суммы при
стремлении диаметров всех частей
поверхноси к нулю, если этот предел
существует, конечен и не зависит от
количества разбиений и выбора промежуточных
точек. Обозначение: .
Формулы для вычисления:
.
Формулы для вычисления:

где
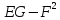 -
первая квадратичная форма поверхности,
-
первая квадратичная форма поверхности,
 .
.
Второго рода:
Пусть дано векторное поле
a=(P,Q,R),
двухсторонняя поверхностьSс выбранным направлением нормалиn,
разобьемSнаkчастей, выберемkточек ,
составим интегральную сумму , где
,
составим интегральную сумму , где .
Поверхностным интегралом второго рода
называется предел интегральной суммы
при стремлении наибольшего диаметра
разбиений к нулю, если он существует,
конечен и не зависит от количества
разбиений и выбора промежуточных точек.
Обозначение:
.
Поверхностным интегралом второго рода
называется предел интегральной суммы
при стремлении наибольшего диаметра
разбиений к нулю, если он существует,
конечен и не зависит от количества
разбиений и выбора промежуточных точек.
Обозначение: .
.
27.Теоремы Остроградского-Гаусса и Стокса.
Рассмотрим тело (V), ограниченное куочно-гладкими поверхностями
 и
цилиндрической поверхностью
и
цилиндрической поверхностью ,
образующие которой параллельны осиZ.
Пусть в области (V) определена
некоторая функцияR(x,y,z),
непрерывная вместе со своей производной
,
образующие которой параллельны осиZ.
Пусть в области (V) определена
некоторая функцияR(x,y,z),
непрерывная вместе со своей производной во
всей области (V), включая
ее границу, тогда имеет место формула
во
всей области (V), включая
ее границу, тогда имеет место формула ,
причем (S) – поверхность,
ограничивающая тело и интеграл справа
распространен на внешнюю её сторону.
Аналогично, имеют место формулы
,
причем (S) – поверхность,
ограничивающая тело и интеграл справа
распространен на внешнюю её сторону.
Аналогично, имеют место формулы
 ,
, .
Сложив все три формулы мы придем к общей
формуле Остроградского-Гаусса:
.
Сложив все три формулы мы придем к общей
формуле Остроградского-Гаусса:
 .
В случае поверхностного интеграла
.
В случае поверхностного интеграла .
Стоящее под знаком тройного интеграла
выражение называется дивергенцией
вектораA. Тогда, формула
Остроградского-Гаусса перепишется в
виде
.
Стоящее под знаком тройного интеграла
выражение называется дивергенцией
вектораA. Тогда, формула
Остроградского-Гаусса перепишется в
виде .
.
Ф-ла Стокса: Пусть S– простая гладкая поверхность,
ограниченная контуром Г,n– нормаль к поверхности. Еслиa=(P,Q,R),
тогда - ф-ла
Стокса.
ф-ла
Стокса.
Или .
.
