
- •Список вопросов к экзамену по математическому анализу
- •2. Критерий Коши сходимости знакопостоянного ряда.
- •3. Признаки сравнения знакопостоянных рядов.
- •4. Знакопеременные ряды. Абсолютная и условная сходимость ряда.
- •5. Признаки Лейбница, Абеля и Дирихле сходимости знакопеременных рядов.
- •6. Действия над рядами. Сумма и произведение рядов.
- •7. Функциональные ряды. Область сходимости функционального ряда.
- •8. Равномерная сходимость. Мажорантный признак Вейерштрасса.
- •9. Степенные ряды. Интервал и радиус сходимости. Ряд Тейлора.
- •10. Ряд Фурье. Условие поточечной сходимости.
- •11.Ряд Фурье. Условие равномерной сходимости.
- •12.Представление функции в виде интеграла Фурье
- •13. Преобразование Фурье
- •14. Собственные интегралы, зависящие от параметра. Предельный переход под знаком интеграла.
- •15.Дифференцирование и интегрирование под знаком интеграла
- •16. Г- и в- функции Эйлера и их основные свойства.
- •17.Двойной интеграл. Теорема о среднем.
- •18. Сведение двойного интеграла к повторному.
- •19. Приложения двойного интеграла.
- •20. Замена переменных в двойном интеграле.
- •21.Тройной интеграл. Приложения тройного интеграла.
- •22.Сведение тройного интеграла к повторному.
- •23.Замена переменных в тройном интеграле.
- •24.Криволинейные интегралы первого и второго рода.
- •25.Теорема Грина.
- •26.Поверхностные интегралы первого и второго рода.
- •27.Теоремы Остроградского-Гаусса и Стокса.
- •28.Элементы теории поля. Дифференциальные векторные операции.
20. Замена переменных в двойном интеграле.
Рассмотрим двойной интеграл
 где
область (D) ограничена
кусочно-гладким контуром (S),
а функцияf(x,y)
непрерывна в этой области. Предположим,
что область (D) связана
формулами
где
область (D) ограничена
кусочно-гладким контуром (S),
а функцияf(x,y)
непрерывна в этой области. Предположим,
что область (D) связана
формулами .
Интегральная сумма
.
Интегральная сумма ,
,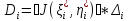 ,
где
,
где -
некоторая определенная точка области
-
некоторая определенная точка области .
Получим
.
Получим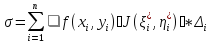 .
Точка
.
Точка берется
в области
берется
в области произвольно,
пользуясь этим получим:
произвольно,
пользуясь этим получим: .
Тогда сумма примет вид
.
Тогда сумма примет вид ,
которая, очевидно, является интегральной
суммой для интеграла
,
которая, очевидно, является интегральной
суммой для интеграла .
Таким образом,
.
Таким образом, .
.
21.Тройной интеграл. Приложения тройного интеграла.
Пусть
в некоторой пространственной области
(V) задана функцияf(x,y,z).
Разобьем эту область на конечное число
частей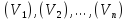 .
В пределахi-го элемента
возьмем произвольные точки
.
В пределахi-го элемента
возьмем произвольные точки ,
значение ф-ции в этой точке
,
значение ф-ции в этой точке умножим
на объем
умножим
на объем и
составим интегральную сумму
и
составим интегральную сумму .
Конечный предел этой суммы при стремлении
к нулю наибольшего из диаметров всех
областей
.
Конечный предел этой суммы при стремлении
к нулю наибольшего из диаметров всех
областей называется
тройным интегралом функции в области
(V), если он непрерывен,
конечен и не зависит от количества и
диаметра разбиений. Обозначение
называется
тройным интегралом функции в области
(V), если он непрерывен,
конечен и не зависит от количества и
диаметра разбиений. Обозначение .
.
Св-ва тройных интегралов:
1)Существование и величина тройного интеграла не зависят от значений, принимаемых фунецией вдоль конечного числа поверхностей с объемом 0.
2)Если
(V)=(V')+(V''),
то ,
причем из существования интеграла слева
вытекает существование интегралов
справа и наоборот.
,
причем из существования интеграла слева
вытекает существование интегралов
справа и наоборот.
3)Если
k=const, то
4)
Если выполняется неравенство
 ,
то
,
то
Имеет место неравенство

Если функция удовлетворяет неравенству
 ,
то
,
то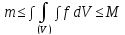 ,
,
иными
словами, имеет место теорема о среднем
значении
 .
.
Механические приложения:
Обозначим
через
 плотность
распределения масс в произвольной точке
тела (V), явл. Функцией от
координат точки. Для величины всей массы
будем иметь
плотность
распределения масс в произвольной точке
тела (V), явл. Функцией от
координат точки. Для величины всей массы
будем иметь .
.
Статические
моменты:
 .
.
Координаты
центра тяжести:
 ,
, ,
, .
.
В
случае однородного тела:
 ,
, ,
, .
.
Моменты
инерции относительно осей координат:
 ,
, ,
, .
.
Относительно
координатных плоскостей:
 ,
, ,
, .
.
Пусть
массы, заполняющие тело (V),
оказывают притяжение на точку по
закрну Ньютона. Сила притяжения со
стороны элементаdmмассы
имеет на оси координат проекции
по
закрну Ньютона. Сила притяжения со
стороны элементаdmмассы
имеет на оси координат проекции ,
, ,
, ,
где
,
где -
расстоение элемента до точкиA.
Получим:
-
расстоение элемента до точкиA.
Получим: ,
, ,
, .
Аналогично определяется и потенциал
тела на точку:
.
Аналогично определяется и потенциал
тела на точку: .
.
22.Сведение тройного интеграла к повторному.
Если
функция f(x,y,z)
определена в области (V),
то вместо неё следует ввести функциюf*(x,y,z),
определенную в объемлющем (V)
прямоугольном параллелепипеде (T),
полагаяf*(x,y,z)=f(x,y,z)
в (V) иf*(x,y,z)=0
вне (V). Пусть тело (V)
содержится между плоскостями и
каждой параллельною им плоскостью,
отвечающей фиксированному значениюx,
пересекается по некоторой фигуре,
имеюшей площадь, обозначим её проекцию
на плоскостьyz
и
каждой параллельною им плоскостью,
отвечающей фиксированному значениюx,
пересекается по некоторой фигуре,
имеюшей площадь, обозначим её проекцию
на плоскостьyz .
Пусть, далее, тело ограничено снизу и
сверху пов-тями
.
Пусть, далее, тело ограничено снизу и
сверху пов-тями проектирубщимися
на пл-тьxyв некоторую
фигуру (D), ограниченной
кривой (K). Имеем:
проектирубщимися
на пл-тьxyв некоторую
фигуру (D), ограниченной
кривой (K). Имеем: .
Если область (D) представляет
собой криволинейную трапецию, ограниченную
кривыми
.
Если область (D) представляет
собой криволинейную трапецию, ограниченную
кривыми и
прямыми
и
прямыми ,
то, заменяя двойной интеграл повторным,
получим
,
то, заменяя двойной интеграл повторным,
получим
23.Замена переменных в тройном интеграле.
Пусть
между областями (D) и пространствxyzи
пространствxyzи существует
соответствие. Покажем, что имеет место
равенство:
существует
соответствие. Покажем, что имеет место
равенство: где
где .
Разложив кусочно-гладкими поверхностями
области (D) и
.
Разложив кусочно-гладкими поверхностями
области (D) и на
элементарные части
на
элементарные части ,
получим
,
получим ,
где
,
где -
некоторая точка области
-
некоторая точка области ,
не зависящая от нашего выбора. Возьмем
соответствующую точку
,
не зависящая от нашего выбора. Возьмем
соответствующую точку области
области ,
т. е. положим
,
т. е. положим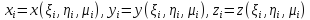 и
составим интегральную сумму для первого
из интегралов
и
составим интегральную сумму для первого
из интегралов .
Подставив соответствующие значения,
придем к сумме
.
Подставив соответствующие значения,
придем к сумме ,
которая, очевидно, является условием
для второго интеграла.
,
которая, очевидно, является условием
для второго интеграла.
