14. Собственные интегралы, зависящие от параметра. Предельный переход под знаком интеграла.

Пусть на множестве Yопределены функциии,, а на множестве- функцияf(x,y).

Определение: Интегралы вида (1)в частности, интегралы(2), называются интегралами, зависящими от параметраy. Подстановкасводит интеграл вида (1) к виду (2).

Теорема: Пусть функции инепрерывна на отрезке [c,d],. Если функцияf(x,y) непрерывна на множестве, то функциянепрерывна на отрезке [c,d]. Таким образом, в этом случае для любой точкиимеет место равенство

Теорема: Если функция f(x,y) определена на прямоугольнике, если она при любом фиксированномнепрерына поxна отрезке [a,b] и, то. Эта теорема представляет собой достаточное условие, при котором возможен предельный переход под знаком интеграла.

15.Дифференцирование и интегрирование под знаком интеграла

Теорема: Если функция f(x,y) непрерывна на прямоугольнике, то

Теорема (правило Лейбница): Если функция f(x,y) и ее частная производнаянепрерывны на прямоугольникеP, то.

16. Г- и в- функции Эйлера и их основные свойства.

Интеграл зависящий от параметраs, называется гамма-функцией, а интегралзависящий от параметровpиq, называется бета-функцией. Гамма-функция и бета-функция называются эйлеровыми интегралами. Разобьем интеграл на дваи заметим, что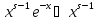при. Так как интегралсходится приs> 0 и расходится при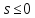, а интегралсходится, то формула для определения гамма-функции Г(s) имеет смысл только приS>0. Иначе говоря, еслиS> 0, то интеграл Г(s) сходится, если же, то интеграл расходится. Аналогично, где. Поскольку интегралсходится приp>0 и расходится при, а интегралсходится приq>0 и расходится при, то формула для определенияB(p,q) имеет смысл только приq>0 иp>0, т.е. при этих значениях параметров интеграл сходится, а при иных — расходится.

17.Двойной интеграл. Теорема о среднем.

Пусть в области (P) определена функцияf(x,y). Разобьем область (P) сетью кривых на конечное число областей. В пределахi-й элементарной областивозьмем произвольные точки, значение функции в этой точкеумножим на площадьсоответствующей области и все подобные произведения сложим. Полученную суммубудем называть интегральной суммой для функцииf(x,y) в области (P). Обозначим черезнаибольший из диаметров частичных областей. Двойным интегралом называется предел, если он существует, конечен и не зависит от количества разбиений и выбора промежуточных точек.

Теорема о среднем: Если интегрируема в (P) функцияf(x,y) удовлетворяет неравенству, то. Если черезобозначить среднее отношение, то получим другую запись неравенства. Должна найтись такая точка, что, тогда формула принимает вид.

18. Сведение двойного интеграла к повторному.

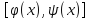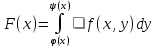Если функция fзадана на множествеи при каждоминтегрируема поyна отрезке, то функцияназывается интегралом, зависящим от параметра, а интегралназывается повторным интегралом.

Теорема: Если функция fнепрерывна на множествеE, то. Если множествоEудолетворяет относительноyусловиям, аналогичнымx,- непрерывные на отрезке [c,d] функции, то в случае непрерывности на множествеEфункцииfбудем иметь

19. Приложения двойного интеграла.

Все геометрические и механические величины, связанные с плоским непрерывным распределением масс вдоль некоторой области выражаются двойными интегралами, распространенными на эту фигуру. В частности, величина распространенной массы выражается по заданной плотности распределения , так.

Выделяя элементарную часть dPфигурыP, которое позволяет дать для элеметаdQискомой величиныQприближенное значение видаdQ=q(M)dP. Тогда точное значение выразится формулой. В силу этого: Статические моменты сил:

Моменты инерции

Координаты центра тяжести фигуры:

В случае однородной фигуры: