10. Ряд Фурье. Условие поточечной сходимости.

Ряд вида называются тригонометрическими рядами Фурье, где- коэффициенты Фурье ф-цииf.

Лемма: Если функция fабсолютно интегрируема на отрезке, то интегралысходятся или расходятся одновременно.

Теорема (признак Дини): Пусть функция f-- периодическая и абсолютно интегрируемая на периоде. Тогда еслиxявляется точкой непрерывности или точкой разрыва первого рода функцииfи интегралабсолютно сходится, то ряд Фурье функцийfсходится в точкеXк значению, в частности, в точке непрерывности — к значениюf(x) функцииfв этой точке.

Следствие 1: Если f-- периодическая абсолютно интегрируемая на периоде функция и в точкеxсуществует конечные односторонние производныеи, то ряд Фурье функцииfсходится в точкеxк значению.

Следствие 2: Ряд Фурье кусочно дифференцируемой на отрезке функцииfсходится в каждой точке интервалак значению, а в точках- к значению. Отсюда следует, что ряд Фурье непрерывной кусочно дифференцируемой и- периодической функции сходится во всех точках числовой оси к самой функции.

11.Ряд Фурье. Условие равномерной сходимости.

Теорема: Если непрерывная и кусочно-гладкая на отрезке [-l,l] функцияf(x) имеет равные значения на концах этого отрезкаf(-l)=f(l), то её тригонометрический ряд Фурье

, где,

, сходится равномерно на этом отрезке, причемS(x)=f(x) в каждой точке отрезка [-l,l].

Замечание: Равенство значений ф-ции f(x) на концах отрезка [-l,l] является необходимым условием того, что тригонометрический ряд Фурье функцииf(x) сходился к ней на концах этого отрезка.

Теорему можно сформулировать иначе. Заметим, что если ф-я f(x) непрерывна на отрезке [-l,l] и имеет равные значения на его концах, то при её периодическом продолжении с периодом 2lполучается ф-я, непрерывная на все осиx. Назовем ф-юf(x) кусочно-гладкой на все осиx, если она является кусочно-гладкой на каждом конечном отрезке осиx. Сформулируем теорему: Если периодическая ф-яf(x) с периодом 2lявлятся непрерывной и кусочно-гладкой на все осиx, то ее тригонометрический ряд Фурье сходится к ней равномерно на все оси.

12.Представление функции в виде интеграла Фурье

Пусть функция Fзадана на всей числовой прямойRи абсолютно интегрируема на ней. Сопоставим функцииfинтеграл, где,. Интеграл аналогичен ряду Фурье периодической функции(суммирование заменено интегрированием). Функцииa(y) иb(y) в подынтегральном выражении аналогичны коэффициентам Фурье. Подставив коэф-ты в подынтегральное выражение получим

Определение: Интеграл называется интегралом Фурье функцииf.

Теорема: Если функция fабсолютно интегрируема на всей числовой осиR, то в каждой точке, в которой существуют, имеет место равенство

13. Преобразование Фурье

Отображение F, ставящее в соответствие абсолютно интегрируемой на всей числовой оси функцииfфункцию, обозначаемуюFfилии задаваемую равенствомназывается преобразованием Фурье, а отображение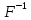, ставящее в соответствие абсолютно интегрируеомй на все оси функцииfфункциюf, задаваемую равенством

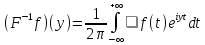- обратным преобразованием Фурье. ФункцияFfназывается образом Фурье функцииf. Если функция принимает только действительные значения, то оба преобразования фурье принимают комплексные значения. Оба интеграла абсолютно сходятся, посколькуто, а интегралпо условию сходится.

Свойства преобразований Фурье:

1)Если функция fабсолютно интегрируема на всей числовой осиR, то её преобрахование ФурьеFfявляется ограниченной непрерывной наRфункцией, стремящейся к нулю, когда её аргумент стремится к бесконечности; при этом для любоговыполняется неравенство

Следствие: Если последовательность абсолютно интегрируемых функций сходится в среднем на числовой осиRк абсолютно интегрируемой функции, то последовательность пребразований Фурье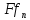функцийсходится равномерно на всей числовой осиRк преобразованию ФурьеFfфункцииf.

2)Если

-функция fнепрерывна и абсолютно интегрируема на числовой оси

-её производная f' кусочно непрерывна на любом конечном отрезке и также абсолютно интегрируема на числовой оси;

то (Ff')(y)=iy(Ff)(y)

3)Если функция f(x) непрерывна, а функцииf(x),xf(x),....,f(x) абсолютно интегрируемы на всей числовой оси, то преобразование Фурье функцииf(x) являетсяnраз дифференцируемой на всей числовой оси функцией и