6. Действия над рядами. Сумма и произведение рядов.

Теорема: Линейная комбинация абсолютно сходящихся рядов является абсолютно сходящимся рядом.

Доказательство: Если ряды иабсолютно сходится, а, то сходится и ряд. Отсюда в силу неравенств, по признаку сравнения следует сходимость ряда, т. е. абсолютная сходимость ряда.

Если ряд абсолютно сходится, то любой ряд , составленный из тех же членов, что и данный ряд, но взятый в другом порядке также абсолютно сходится и имеет ту же сумму

Если ряды ,абсолютно сходятся, то ряд, составленный из всевозможных попарных произведенийчленов этих рядов, также абсолютно сходится, причем его суммаsравна произведению сумм данных рядов: если,, то, т. е. абсолютно сходящиеся ряды можно перемножать почленно.

7. Функциональные ряды. Область сходимости функционального ряда.

Пусть на некотором множестве Xзадана последовательность функций, принимающих числовые значения. Элементы множестваXбудем называть точками. Последовательность называется ограниченной на множествеX, если существует такое числоC> 0, что для всехn= 1,2,... и всех точеквыполняется неравенство. Последовательностьназывается сходимостью на множествеX, если при любом фиксированномчисловая последовательностьсходится. Если последовательностьсходится на множествеX, то функцияf, определенная при каждомравенствомназывается пределом последовательности.

Пусть на множестве Xзадана последовательность числовых функцийМножество всех числовых рядовв каждом из которых точкапроизвольно фиксирована, называется рядомна множествеX, а функции,-его членами.

Аналогично случаю числовых рядов сумма , называется частичной суммой рядаn-го порядка, а ряд- егоn-м остатком.

Ряд называется сходящися на множестве X, если последовательностьего частичных сумм сходится на этом множестве. При этом предел частичных суммназывается суммой ряда. В этом случае пишути говорят, что функцияs(x) раскладывается в ряд. Если рядПри любом фиксированномсходится абсолютно, то он называется абсолютно сходящимся на множествеX.

8. Равномерная сходимость. Мажорантный признак Вейерштрасса.

Функциональная последовательность называется равномерно сходящейся к функции fна множествеX, если для любого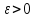существует такой номер, что для всех точеки всех номероввыполняется неравенство. Очевидно, что если последовательностьравномерно сходится на множествеXк функцииf, то пишут, если последовательность сходится равномерно кfна указанном множестве, то пишут. Если последовательностьтолько сходится к функцииfна множествеX, то для каждой точкисуществует свой номер, для которого привыполняется неравенствои может оказаться, что для всех точекневозможно подобрать общий номер, обладающий указанным свойством. Равномерная же сходимосто последовательностик функцииfозначает, что, какое бы числони задать, можно подобрать такой номер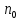, что в любой точкезначение функциибудет отличаться от значения функцииfменьше, чем на.

Ряд называется равномерно сходящимся на множествеx, если наxравномерно сходится последовательность его частичных сумм.

Теорема(признак Вейерштрасса): Если числовой ряд , сходится и для всехи для всехn= 1,2,... выполняется неравенство, то ряд абсолютно и равномерно сходится на множествеX.

9. Степенные ряды. Интервал и радиус сходимости. Ряд Тейлора.

Степенным рядом называется ряд вида числа, называются коэффициентами ряда. С помощью заменыряд может быть преобразован к виду.

Число R=supX(конечно или бесконечное) называется радиусом сходимости ряда, а круг- его кругом сходимости.

Пусть R— радиус сходимости ряда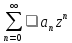. Тогда если |z|>R, то ряд сходится абсолютно, если |z|>R, то ряд расходится, а если, то в кругерядсходится равномерно.

Функция fназывается аналитической в точке, если в некоторой окрестности этой точки функцияfраскладывается в степенной ряд.

Лемма: Радиусы сходимости соответственно рядов,равны.

Теорема: Если функция fраскладывается в окрестности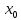в степенной ряд с радиусом сходимостиR, то

1)Функция fимеет на интервалепроизводные всех порядков, которые могут быть найдены из рядапочленным дифференцированием:

2)Для любого

3)Эти ряды имеют одинаковые радиусы сходимости. В целом, внутри интервала сходимости степенного ряда ряд можно почленно интегрировать и дифференцировать любое число раз.

Теорема: Если функция fраскладывается в некоторой окрестности точкив степенной ряд, то, следовательно, справедлива формула

Пусть действительная функция fопределена в некоторой окрестности точкии имеет в этой точке производные всех порядков. Тогда рядназывается её рядом Тейлора в точке.