Список вопросов к экзамену по математическому анализу

(ФКН, МКН, 3 семестр, 2 курс).

1. Знакопостоянные ряды. Необходимое условие сходимости ряда.

2. Критерий Коши сходимости знакопостоянного ряда.

3. Признаки сравнения знакопостоянных рядов.

4. Знакопеременные ряды. Абсолютная и условная сходимости ряда.

5. Признаки Лейбница, Абеля и Дирихле сходимости знакопеременных рядов.

6. Действия над рядами. Сумма и произведение рядов.

7. Функциональные ряды. Область сходимости функционального ряда.

8. Равномерная сходимость. Мажорантный признак Вейерштрасса

9. Степенные ряды. Интервал и радиус сходимости. Ряд Тейлора.

10. Ряд Фурье. Условие поточечной сходимости.

11. Ряд Фурье. Условие равномерной сходимости.

12. Представление функции в виде интеграла Фурье.

13. Преобразование Фурье.

14. Собственные интегралы, зависящие от параметра. Предельный переход под знаком интеграла.

15. Дифференцирование и интегрирование под знаком интеграла.

16. Г- и В- функции Эйлера и их основные свойства.

17. Двойной интеграл. Теорема о среднем.

18. Сведение двойного интеграла к повторному.

19. Приложения двойного интеграла

20. Замена переменных и двойном интеграле.

21. Тройной интеграл. Приложения тройного интеграла.

22. Сведение тройного интеграла к повторному.

23. Замени переменных и тройном интеграле.

24. Криволинейные интегралы первого и второго рода.

25. Теорема Грина.

26. Поверхностные интегралы первого и второго рода.

27. Теорема Остроградского-Гаусса и Стокса (без доказательства).

28. Элементы теории поля. Дифференциальные векторные операции.

1. Знакопостоянные ряды. Необходимое условие сходимости ряда.

Пара последовательностей , гденазывается рядом (а также бесконечной суммой) и обозначаетсяили. Элементы последовательностиназываются членами ряда, а элементы последовательности- его частичными суммами. Если существует конечный предел, то он называется суммой ряда. В этом случае ряд называется сходящимся и пишут. Если последовательность частичных сумм не стремится к конечному пределу, то ряд называется расходящимся. Очевидно, что. Каждая из последовательностейиоднозначно определяет другую. Таким образом, чтобы задать ряд, достаточно задать одну из последовательностейили. В этом случае изучение рядов равносильно изучению последовательностей.

Теорема (необходимое условие сходимости ряда): Если ряд сходится, то последовательность его членов стремится к нулю.

Доказательство: Если ряд сходится, т. е. Существует конечный пределего частичных сумм, то из равенстваследует, что.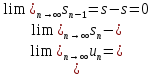

2. Критерий Коши сходимости знакопостоянного ряда.

Теорема:

Для того, чтобы ряд сходился, необходимо и достаточно, чтобы для любогосуществовало такое, что для всехи всех целыхимеет место неравенство

Доказательство: Это утверждение следует из критерия Коши существования конечного предела последовательности, примененного к последовательности частичных сумм данного ряда,

Замечание: при p=0 из теоремы следует, что если рядсходится, то для любогосуществует такоей номер, что для всехвыполняется неравенство, а это означается, что. Таким образом, получаем еще одно доказательство теоремы.