3. Теорема существования и единственности решения дифференционального уравнения с переменными коэффициентами.

3.1. Постановка задачи

В полосе 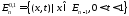рассматривается задача:

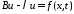37337\* MERGEFORMAT (.)

где

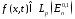
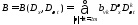
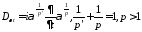
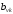-постоянные комплексные коэффициенты;

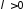- параметр;

-весовая функция

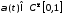
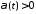при ;

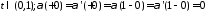Исследуется разрешимость уравнения 337

Решим задачу

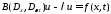38338\* MERGEFORMAT (.)

где область оператора :

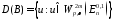
Пространство 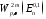, где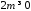-целое,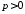-весовое пространство Соболева, в котором содержатся функции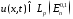, для которых конечна норма:

при

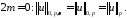
Условие 1. Существует 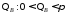такое, что при всех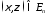и.

3.2. Теорема существования и единственности решения дифференциального уравнения с переменными коэффициентами.

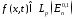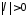Теорема. Пусть выполнено условие 1 и . Тогда при любомсуществует единственное решение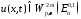, для которых справедлива оценка:

. 39339\* MERGEFORMAT (.)

Доказательство. Рассмотрим функцию:

.

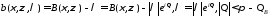Видно, что для любого :

. 40340\* MERGEFORMAT (.)

Из условия 1 вытекает, что:

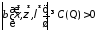при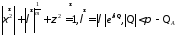. 41341\* MERGEFORMAT (.)

Действительно, из равенства:

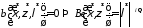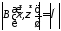, т.е. и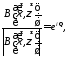

что противоречит условию.

Учитывая 340 и 341, и полагая

,

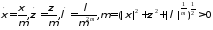получим оценку:

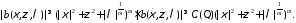
На основании этой оценки можно убедиться, что функция:

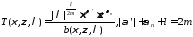
является мультипликатором типа в пространстве.

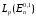Применение теоремы о мультипликаторах дает оценку 339 с константой .

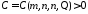3.3. Теорема оценки производных решения.

Теорема. Пусть 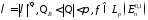. Тогда при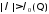выполняются следующие оценки:

42342\* MERGEFORMAT (.)

43343\* MERGEFORMAT (.)

Доказательство. Уравнение 338 продифференцируем по 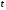. Получим:

.

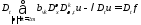Учитывая, что:

,

где 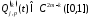, зависит лишь от функции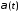и её производных до порядка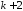получим:

.

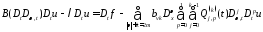Обозначим через:

Пусть 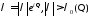. Тогда прииз леммы 1 следует

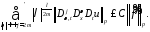44344\* MERGEFORMAT (.)

Используем неравенство:

,

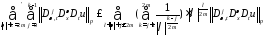и с помощью леммы 1 устанавливаем оценку

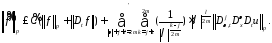45345\* MERGEFORMAT (.)

Дважды продифференцируем по 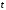исходное уравнение с оператором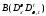. Получим

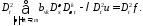
Учитывая, что:

,

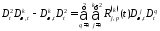где , зависит лишь от функции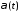и её производных до порядкаполучим:

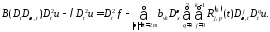
Обозначим через:

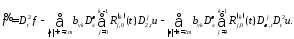
Пусть 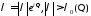. Тогда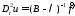из леммы 1 следует:

46346\* MERGEFORMAT (.)

Используем неравенство:

,

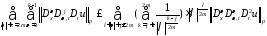Из теоремы 1 следует

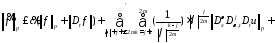47347\* MERGEFORMAT (.)

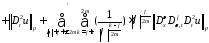
Из неравенства 345, 346, 347 а так же неравенств:

справедливо при всех достаточно больших 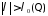, выводим оценку:

Литература

1. ВВС. Уравнения математической физики// В.С Владимиров -. М.Физматлит, 2003. – 286 с.

2. М.Тейлор. Псевдодифференциальные операторы, Москва «Мир» 1985, 490 с.

3. Глушко В.П. Вырождающиеся эллиптические уравнения высокого порядка в пространствах, операторы, граничные задачи // В.П.Глушко, Ю.Б.Савченко, Итоги науки и техники, ВИНИТИ-М 1985,-т.23,-с. 125-218

4. Савченко Ю.Б. Весовые мультипликаторы в пространствах Гёльдера//Ю.Б. Савченко, С.А. Ткачёва. – Труды ВВМШ Понтрягинские чтения – ХХI, Воронеж 2010. – с.89-92.

56