
- •Оглавление
- •Введение
- •1.1.2. Преобразование Фурье производной.
- •1.1.3. Преобразование Фурье убывающих функций.
- •1.1.4 Формула обращения преобразования Фурье
- •1.1.5. Преобразование Фурье в пространстве .
- •1.1.6. Преобразование Фурье функции нескольких переменных.
- •1.2. Мультипликаторы Фурье в пространстве
- •2.Пространство основных и обобщенных весовых функций.
- •2.1. Основные весовые функции. Весовые интегральные преобразования ,. Некоторые операции в пространстве
- •2.2 Весовое преобразование Фурье.
- •2.3. Класс весовых мультипликаторов .
- •3. Теорема существования и единственности решения дифференционального уравнения с переменными коэффициентами.
- •3.1. Постановка задачи
- •3.2. Теорема существования и единственности решения дифференциального уравнения с переменными коэффициентами.
- •3.3. Теорема оценки производных решения.
- •Литература
1.1.2. Преобразование Фурье производной.
Пусть
абсолютно интегрируемая функция
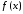 имеет производную при всех
имеет производную при всех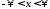 ,
причем
,
причем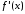 непрерывна и абсолютно интегрируема.
В таком случае
непрерывна и абсолютно интегрируема.
В таком случае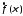 и преобразование Фурье функции
и преобразование Фурье функции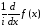 связаны так:
связаны так:
 . 11111\* MERGEFORMAT (.)
. 11111\* MERGEFORMAT (.)
Доказательство.
Действительно, с помощью интегрирования по частям получаем, что
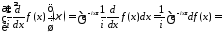
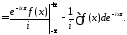
так
как
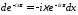 ,
то остается показать, что
,
то остается показать, что при
при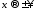 .
.
Поскольку
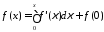 ,
то в силу предложения об абсолютной
интегрируемости
,
то в силу предложения об абсолютной
интегрируемости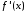 функция
функция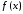 имеет пределы при
имеет пределы при и
и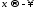 .
Легко увидеть, что хотя бы один из
пределов отличен от нуля, то функция
.
Легко увидеть, что хотя бы один из
пределов отличен от нуля, то функция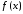 не может быть абсолютно интегрируемой,
следовательно
не может быть абсолютно интегрируемой,
следовательно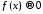 при
при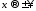 .
Тем самым формула 111 доказана.
.
Тем самым формула 111 доказана.
Формула
111 показывает, что при преобразовании
Фурье операция дифференцирования
переходит в число алгебраическую
операцию умножения на
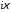 функция
функция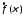 это открывает широкие возможности для
применения преобразования Фурье при
исследовании дифференциальных операторов.
это открывает широкие возможности для
применения преобразования Фурье при
исследовании дифференциальных операторов.
1.1.3. Преобразование Фурье убывающих функций.
Преобразование
Фурье
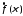 абсолютно интегрируемой функции
абсолютно интегрируемой функции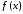 является ограниченной непрерывной
функцией, стремящейся к нулю при
является ограниченной непрерывной
функцией, стремящейся к нулю при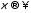 .
Формальное дифференцирование по
переменному
.
Формальное дифференцирование по
переменному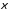 интеграла 14, определяющего
интеграла 14, определяющего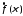 , приводит к следующему выражению:
, приводит к следующему выражению:
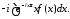
Предположим,
что функция
 абсолютно интегрируема, тогда этот
интеграл, зависящий от параметра
абсолютно интегрируема, тогда этот
интеграл, зависящий от параметра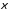 ,
равномерно сходится.
,
равномерно сходится.
Применяя
теорему о дифференцировании по параметру
несобственных интервалов получим, что
функция
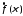 имеет производную и
имеет производную и

Так
как слева стоит преобразование Фурье
функции
 , то мы получим формулу
, то мы получим формулу
 12112\* MERGEFORMAT (.)
12112\* MERGEFORMAT (.)
которая
показывает, что операция умножения на
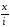 переходит после преобразования Фурье
в операцию
переходит после преобразования Фурье
в операцию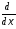 .
Если вместо с функцией
.
Если вместо с функцией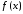 абсолютно интегрируемыми являются и
функции
абсолютно интегрируемыми являются и
функции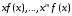 ,
то интеграл в 14 можно дифференцировать
,
то интеграл в 14 можно дифференцировать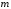 раз.
раз.
Таким
образом, чем более сильные условия
убывания на бесконечности мы накладываем
на функция
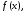 тем белее гладкая получается функция
тем белее гладкая получается функция .
.
1.1.4 Формула обращения преобразования Фурье
Часто
возникает такая ситуация, что мы не
знаем самой функции f(x),
но можем найти
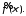 В таком случае возникает задача обращения
преобразования Фурье , то есть задача
о вычислении функцииf(x)
в точке x
по известной функции
В таком случае возникает задача обращения
преобразования Фурье , то есть задача
о вычислении функцииf(x)
в точке x
по известной функции
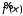 .
Следующая теорема дает решение этой
задачи при дополнительном предложении
о существовании производной функции
.
Следующая теорема дает решение этой
задачи при дополнительном предложении
о существовании производной функции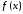 в точке
в точке .
.
Теорема
1.
Если функция
 абсолютно интегрируема и существует
производная
абсолютно интегрируема и существует
производная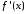 ,
то
,
то
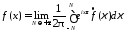 .
.
Доказательство. Положим
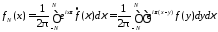 .
.
Меняя порядок интегрирования в последнем интеграле, получим, что
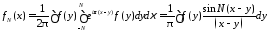 .
13113\* MERGEFORMAT (.)
.
13113\* MERGEFORMAT (.)
Поскольку
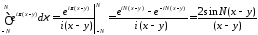 .
.
Возможность изменения порядка интегрирования легко обосновать, используя теоремы математического анализа о перемене порядка интегрирования в кратных интегралах.
Прежде,
чем продолжать дальше доказательство,
заметим, что для любой абсолютно
интегрируемой функции
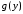
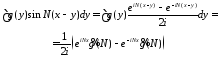 14114\* MERGEFORMAT (.)
14114\* MERGEFORMAT (.)
и
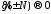 при
при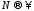 в силу леммы 1.
в силу леммы 1.
Если мы положим,
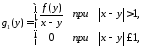
то
из 114 получим, что при
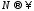
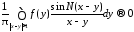 .
15115\* MERGEFORMAT (.)
.
15115\* MERGEFORMAT (.)
Если же положим
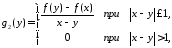
то
из 114 получим, что при
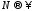
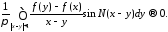 16116\* MERGEFORMAT (.)
16116\* MERGEFORMAT (.)
Абсолютная
интегрируемость
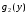 легко проверяется с помощью критерия
интегрируемости, если заметить, что в
силу нашего предположения о существовании
производной
легко проверяется с помощью критерия
интегрируемости, если заметить, что в
силу нашего предположения о существовании
производной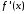 функция
функция имеет предел
имеет предел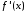 при
при и, следовательно, ограничена в некоторой
окрестности точки
и, следовательно, ограничена в некоторой
окрестности точки .
.
Из
соотношений 113, 115, 116 мы получаем, что
при

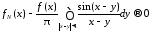 .
.
Остается заметит, что при
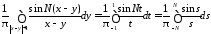 ,
,
и
при
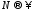
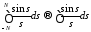 ,
,
причем
несобственный интеграл
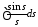 по всей оси сходится и равен
по всей оси сходится и равен .
.
Следствие.
Если выполнены условия теоремы и, кроме
того, функция
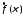 абсолютно интегрируема, то
абсолютно интегрируема, то
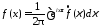 17117\* MERGEFORMAT (.)
17117\* MERGEFORMAT (.)
Формула
117 дает решение задачи обобщения
преобразования Фурье. В связи с этим
для абсолютно интегрируемой функции
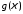 функцию
функцию
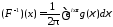
называется
обратным преобразованием Фурье от
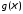 .
.
Легко видеть, что
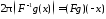 18118\* MERGEFORMAT (.)
18118\* MERGEFORMAT (.)
