
- •Оглавление
- •Введение
- •1.1.2. Преобразование Фурье производной.
- •1.1.3. Преобразование Фурье убывающих функций.
- •1.1.4 Формула обращения преобразования Фурье
- •1.1.5. Преобразование Фурье в пространстве .
- •1.1.6. Преобразование Фурье функции нескольких переменных.
- •1.2. Мультипликаторы Фурье в пространстве
- •2.Пространство основных и обобщенных весовых функций.
- •2.1. Основные весовые функции. Весовые интегральные преобразования ,. Некоторые операции в пространстве
- •2.2 Весовое преобразование Фурье.
- •2.3. Класс весовых мультипликаторов .
- •3. Теорема существования и единственности решения дифференционального уравнения с переменными коэффициентами.
- •3.1. Постановка задачи
- •3.2. Теорема существования и единственности решения дифференциального уравнения с переменными коэффициентами.
- •3.3. Теорема оценки производных решения.
- •Литература
2.Пространство основных и обобщенных весовых функций.
2.1. Основные весовые функции. Весовые интегральные преобразования ,. Некоторые операции в пространстве
Введем
основные и обобщенные весовые функции,
определенные на отрезке
 .
В качестве весовой функции будем
использовать функцию
.
В качестве весовой функции будем
использовать функцию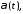
 ,
принадлежащую
,
принадлежащую и удовлетворяющую условиям:
и удовлетворяющую условиям:
 при
при
 ,
,
 ,
,
 ,
,
 ,
,
 .
.

α
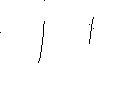

0
1
t
Рассмотрим функцию:
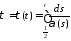 . 32232\* MERGEFORMAT (.)
. 32232\* MERGEFORMAT (.)
Т.к.
функция
 является монотонной
является монотонной ,
то существует обратная к ней функция
,
то существует обратная к ней функция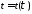
Таким
образом,
 взаимно однозначно отображает
взаимно однозначно отображает на
на
Для
некоторой функции
 ,
,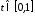 определим функцию
определим функцию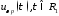 по формуле [3]:
по формуле [3]:
 ,
33233\* MERGEFORMAT (.)
,
33233\* MERGEFORMAT (.)
где
 обратная функция к функции
обратная функция к функции .
.
 . 34234\* MERGEFORMAT (.)
. 34234\* MERGEFORMAT (.)
Возьмем
функцию
 и
и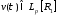 ,
для этих функций будут справедливы
неравенства:
,
для этих функций будут справедливы
неравенства:
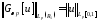 ,
,
 ,
,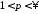 35235\* MERGEFORMAT (.)
35235\* MERGEFORMAT (.)
Действительно:




Дадим определение пространства основных весовых функций.
Функция
 принадлежит пространству
принадлежит пространству если соответствующая функция
если соответствующая функция принадлежит
принадлежит ,
т.е.
,
т.е.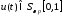 ,
если
,
если ,
или
,
или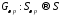 ,
где
,
где -
оператор, заданный следующим образом:
-
оператор, заданный следующим образом:
 .
.
Последовательность
функций
 в множестве
в множестве при
при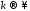 ,
если последовательность функции
,
если последовательность функции сходится к
сходится к в пространстве
в пространстве при
при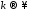 .
Множество
.
Множество ,
наделенное топологией по предыдущему
определению, будем называть пространством
основных весовых функций и обозначать
,
наделенное топологией по предыдущему
определению, будем называть пространством
основных весовых функций и обозначать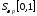 .
.
На
этом множестве вводиться семейство
норм, зависящих от
 следующим образом:
следующим образом:
 .
.
 ;
;
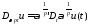 ;
;
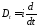 ;
;
 .
.
Изучены
некоторые непрерывные операции в
пространстве основных весовых функций
 .
.
Будем
говорить, что функция
 ,
, принадлежит к классу
принадлежит к классу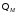 ,
если функция
,
если функция и все ее производные имеют степенной
рост.
и все ее производные имеют степенной
рост.
Функция
 принадлежит классу
принадлежит классу , если функция
, если функция принадлежит классу
принадлежит классу по переменной
по переменной .
.
1)Опереция
умножения на функцию класса

Пусть
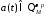 ,
тогда
,
тогда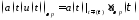 .
.
Функция
 по переменной
по переменной ;
;
 .
.
С
учетом свойств пространств можно
сказать, что операция умножения является
линейной и непрерывной из
 в
в .
.
2) Весовое дифференцирование.
На
функциях
 определим операцию весового
дифференцирования
определим операцию весового
дифференцирования по формуле:
по формуле:
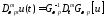 ,
,
где
 ,
, ,
,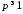 ,
,


Действительно:

 .
.
2.2 Весовое преобразование Фурье.
Для
 определяем весовое преобразование
Фурье [3]
определяем весовое преобразование
Фурье [3]
 ,
,
где
 -обычное преобразование Фурье по
переменной
-обычное преобразование Фурье по
переменной ,
а оператор
,
а оператор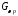 определен на функциях
определен на функциях по формуле:
по формуле:

где
 -обратная
функция в функции
-обратная
функция в функции .
.
Определим весовое преобразование через интеграл:


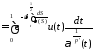
Из
определения
 (множество бесконечно дифференцируемых
функций переменной
(множество бесконечно дифференцируемых
функций переменной ,
убывающих быстрее любой отрицательной
степени
,
убывающих быстрее любой отрицательной
степени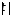 )
и свойств преобразования Фурье на
)
и свойств преобразования Фурье на следует, что
следует, что является линейной непрерывной операцией
из
является линейной непрерывной операцией
из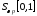 на
на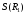 .
.
Обозначим
 .
С помощью обратного преобразования
Фурье находим:
.
С помощью обратного преобразования
Фурье находим: .
Если последнее равенство разделим на
.
Если последнее равенство разделим на и сделаем замену переменных, то получим:
и сделаем замену переменных, то получим:
 .
.
Таким
образом, преобразование
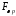 отображает взаимнооднозначно
отображает взаимнооднозначно на
на .
Кроме того, учитывая свойства обычного
преобразования Фурье, можно сказать,
что операция
.
Кроме того, учитывая свойства обычного
преобразования Фурье, можно сказать,
что операция является линейной и непрерывной из
является линейной и непрерывной из на
на ,
а
,
а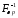 - линейной и непрерывной из
- линейной и непрерывной из на
на .
.
Из
определения
 в связи весового преобразования
в связи весового преобразования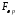 с обычным преобразованием Фурье вытекает,
что
с обычным преобразованием Фурье вытекает,
что
 для
любого
для
любого
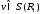
 для
любого
для
любого .
.
Определим теперь весовое преобразование Фурье от производной:
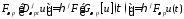 .
.
Действительно:
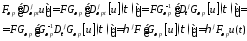
Используя
следующую формулу
 определим производную от весового
преобразования Фурье:
определим производную от весового
преобразования Фурье:
 .
.
Действительно:
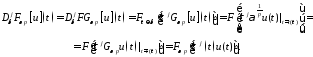
2.3. Класс весовых мультипликаторов .
Теперь
введем обобщенные весовые функции
определенные на отрезке
 .
.
Множество
линейных непрерывных функционалов над
пространством
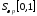 называется множеством весовых обобщенных
функций
называется множеством весовых обобщенных
функций .
.
Функционалы
над
 обозначаются
обозначаются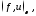 где
где
 .
.
Сходимость
в
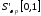 определяется как слабая сходимость
функционалов: последовательность
обобщенных функций
определяется как слабая сходимость
функционалов: последовательность
обобщенных функций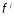 из
из при
при сходится в
сходится в к
обобщенной функции
к
обобщенной функции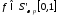 ,
если для любой
,
если для любой :
: при
при .
.
Линейное
множество
 с
введенной на нём сходимостью называется
пространством весовых обобщенных
функций.
с
введенной на нём сходимостью называется
пространством весовых обобщенных
функций.
Пространство
 -пространство
линейных и непрерывных функционалов
над
-пространство
линейных и непрерывных функционалов
над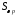 является сопряженным к пространству
является сопряженным к пространству .
.
Определим
операторы
 на
на и
и на
на по формулам:
по формулам:

 ,
,
где
функционал, стоящий в правой (левой)
части первого (второго) равенства
означает функционал над

Докажем предыдущие равенства через интегралы.
Знаем:
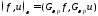
Действительно:




Очевидно,
что
 непрерывная операция из
непрерывная операция из на
на .
.
Определим
преобразование Фурье
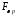 на
на по формуле:
по формуле:
 ,
,
т.е.
это
 на
на по формуле:
по формуле:
 ,
т.е.
,
т.е.
 .
.
 и
и
 -прямое и обратное преобразование Фурье
пространства обобщенных функций
-прямое и обратное преобразование Фурье
пространства обобщенных функций .
.
Одним
из свойств прямого и обратного
преобразования Фурье в
 является легко доказываемое равенство:
является легко доказываемое равенство:
 в
в
 ,
, в
в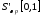 .
.
Пусть
 ,
где
,
где .
Обозначим:
.
Обозначим:
 ,
,
где
 и
и соответственно, прямое и обратное
преобразование Фурье в пространстве
обобщенных функций
соответственно, прямое и обратное
преобразование Фурье в пространстве
обобщенных функций .
.
Обозначим
через
 .
Будем говорить, что функция
.
Будем говорить, что функция принадлежит классу весовых мультипликаторов
принадлежит классу весовых мультипликаторов [4] в пространствах
[4] в пространствах ,
если для любой функции
,
если для любой функции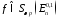 справедлива оценка:
справедлива оценка:
 .
.
Теорема
(о мультипликаторах).
Если функция
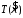 имеет
непрерывные частные производные до
порядка
имеет
непрерывные частные производные до
порядка включительно для всех
включительно для всех ,
и существует положительное число
,
и существует положительное число ,
такое, что для всх мультииндексов
,
такое, что для всх мультииндексов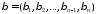 ,
где
,
где принимают значения 0 и 1,
принимают значения 0 и 1,
 ,
,
тогда
функция
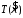 принадлежит классу
принадлежит классу и
и
 ,
,
где
постоянная
 зависит лишь от
зависит лишь от и
и .
.
Доказательство. Учитывая, что
 ,
,
 .
.
Подставляя
значения
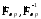 и используя рассуждения, приведенные
в теореме, запишем следующую систему
равенств
и используя рассуждения, приведенные
в теореме, запишем следующую систему
равенств

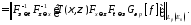
Из
условия теоремы следует, что
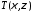 является мультипликатором в
является мультипликатором в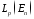 .
Следовательно, из теоремы С.Г. Михлина-
П. И. Лизоркина имеем:
.
Следовательно, из теоремы С.Г. Михлина-
П. И. Лизоркина имеем:
 ,
,
где
постоянная
 зависит лишь от
зависит лишь от и
и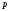 .
Отсюда окончательно получаем:
.
Отсюда окончательно получаем:
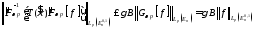 .3631Equation Chapter (Next) Section 3
.3631Equation Chapter (Next) Section 3
